稀疏线性调频步进信号弹道导弹进动微多普勒特征重构与提取方法

朱丰，张群，李松，冯有前，张维强

(1.空军工程大学 信息与导航学院，陕西 西安710077;2.93508 部队，北京100079;3.空军工程大学 防空反导学院，陕西 西安710051;4.空军工程大学 理学院，陕西 西安710051;5.95947 部队，四川 成都610081)

0 引言

弹道导弹进动包括自旋和锥旋两种运动方式。文献［1］分析了锥形目标的锥旋模型及其微多普勒。文献［2］探讨了锥形弹头的进动模型及其微多普勒。近年来，基于高分辨雷达的弹道导弹进动微多普勒特征提取技术逐渐得到了国内外学术界的重视。弹道导弹目标属于小尺寸目标，为利用高分辨雷达技术准确识别出不同的弹道导弹目标，对分辨率要求是比较高的。由高分辨雷达原理知，为获得足够高的距离分辨率，需要发射信号具有很大的带宽，这就对数字信号处理机提出了一定的挑战。为此，学术界提出了线性调频步进信号(FSCS)来合成大带宽［4］。但在利用该信号合成大带宽的工程中，需要发射的线性调频步进信号子脉冲个数较多，很可能出现子脉冲回波丢失或者受损的情况，造成FSCS 频谱的间断，那么如何用较少的FSCS 子脉冲数，即FSCS 频谱稀疏条件下，同样合成大带宽，有效完成微多普勒信息的提取工作有待研究［5］。

压缩感知(CS)理论是近年来信号处理领域中的一个研究热点［6］。利用CS 理论对信号进行处理可以不用满足奈奎斯特采样定理的要求，而获得足够的目标信息，它能以较少的资源完成所需的高分辨合成。本文将CS 理论引入到频谱稀疏FSCS 的高分辨合成中，利用频谱稀疏的FSCS 同样实现高分辨的合成，有效完成微多普勒信息的提取工作。此外，利用CS 理论重构出的结果是由许多冲激函数组成的，这些冲激函数可以有效地抑制谱图中的旁瓣影响［7］，更有利于后续微多普勒信息的提取工作。

本文继续针对高分辨雷达谱图上的弹道导弹进动微多普勒特征提取问题展开一定的研究工作，利用弹道导弹进动(包括锥旋)微多普勒在谱图上的特征曲线的光滑性，提出利用应用数学领域中的动态规划来完成微多普勒信息提取［8］。

1 基于FSCS 的弹道导弹进动微多普勒分析

假设FSCS 脉冲串中包括N 个子脉冲，脉冲间频率步进值为Δf，子脉冲宽度为T1，子脉冲带宽为B1，子脉冲重复间隔为Tr.假设雷达观测时间为T，观测过程中雷达发射MB=「T/(TrN)⏋个脉冲串，即m=1，2，…，MB，「·⏋表示向正无穷大取整。

本文以有翼弹头为例展开相关的分析［2，9］。弹道导弹的进动包括弹头自身围绕重心轴的自旋和锥旋，其中锥旋是指弹头绕对称轴以外的某空间轴线的旋转运动，“自旋”+“锥旋”就是进动。弹头进动时，其与雷达之间的空间几何变换关系如图1所示，其中(U，V，W)为雷达坐标系，其坐标原点为O，雷达位于O 点.(x，y，z)为目标本地坐标系，也称为弹体坐标系［3］，其坐标原点为目标的质心O'，方位角为α'，相对于锥旋轴的仰角β'，O'z 轴为目标对称轴，也是自旋轴，本地坐标系随弹头的运动而运动。设散射点P 在本地坐标系中的初始位置矢量为rp=(xp，yp，zp)，其在不同时刻到雷达的距离为R(m).(X，Y，Z)为参考坐标系，其坐标原点P0(假设为参考点)位于O'z 轴，一般情况下，取自旋轴与锥旋轴的交点为参考坐标系的原点，参考坐标系(X，Y，Z)与雷达坐标系(U，V，W)平行，只随弹头的平动而运动。参考点P0在本地坐标系中的位置矢量r0=(0，0，z0)，参考坐标系中的位置矢量为0 =(0，0，0)，雷达坐标系中的方位角和仰角分别为α 和β，其在不同时刻到雷达的距离为R0(m).

图1 弹道导弹锥形弹头的进动模型Fig.1 Precession model of cone warhead

雷达发射的第m 个脉冲串里的第i 个子脉冲可以表达为

式中:i=0，1，2，…，N-1;m=0，1，2，…，MB-1;

fc+iΔf 是第i 个子脉冲的载频;μ 为线性调频子脉冲的调频斜率。通过一定的处理［10］，可以得到对粗分辨距离像(CRRP)采样后的结果，如下

式中:c 为电磁波的传播速度;σ 为散射点P 的反射系数;RΔ(m)为目标散射点到雷达距离与参考点到雷达距离之差。再对SCRRPi(i;m)做关于i 的N 点IDFT，可得到高分辨距离像(HRRP)，

|SHRRP(kX;m)|即为谱图。从(4)式中可以看出，|SHRRP(kX;m)|的峰值出现在

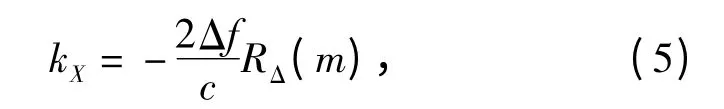
为m 的一个函数。分析弹道导弹进动情况，散射点P 在参考坐标系中初始位置矢量可写为

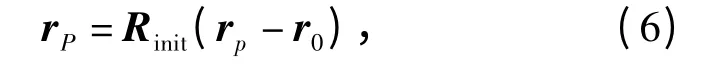
式中Rinit为初始旋转矩阵，即初始时刻本地坐标系到参考坐标系的旋转矩阵［2］

对于进动，m 时刻P 点在参考坐标系中位置矢量为

式中Tconning、Tspinning分别为弹头在参考坐标中的锥旋和自旋矩阵。根据Euler-Rodrigues 绕矢量旋转公式［2］，可得

式中ωc和ωs、1c和1s、Ec和Es分别为锥旋和自旋的旋转角速度、单位矢量及相应的扩充矩阵［3］。

则m 时刻

式中‖‖表示取范数运算。

首先设弹道导弹无自旋，Tspinning=0，分析锥旋。m 时刻，散射点P 在参考坐标系中位置矢量

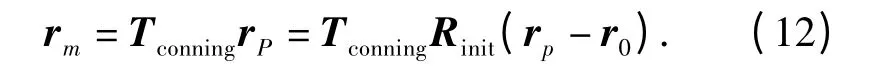
则m 时刻，RΔ(m)可以表示为

因此，各个HRRP 中对应的峰值位置可以表示为

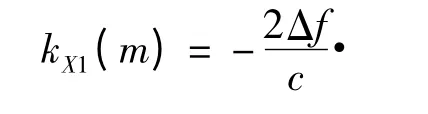
分析(14)式，由于I 和Ec均为常数矩阵，rP为常数向量，因此，kX1随m 的变化规律由sin (ωcm)和cos (ωcm)线性决定。kX1的标量展开式可简记为

式中Z 和φ0均为常数。可见，单散射点在各个HRRP 中对应的峰值位置随m 的变化规律是一条同角频率的正弦曲线，即锥旋微多普勒特征在谱图上表现为一条正弦曲线，且曲线周期为锥旋周期。

下面考察kX1(m)的光滑性，即对kX1(m)求关于自变量m 的导函数，并考察该导函数的连续性。kX1(m)关于自变量m 的导函数可写为

由于

所以kX1(m)关于自变量m 的导函数是连续的，因此，kX1(m)关于自变量m 是光滑的。

当弹道导弹存在自旋和锥旋，即进动情况。这时，各个HRRP 中峰值位置可进一步表示为

令g(m)=(I +L1+L2+L3+L4)rP，可以看出，单散射点的进动微多普勒特征在谱图上表现为正弦曲线的一些组合，包括线性组合和一次乘积组合，因此，进动微多普勒特征曲线具有周期性，且周期为锥旋周期和自旋周期的最小公倍数。

下面考察kX2(m)的光滑性，对kX2(m)求关于自变量m 的导函数来考察导数的连续性。由于kX2(m)的标量展开式过于复杂，因此，考察范数运算符号里面函数的光滑性，即对g(m)求导，得

由于Ec、E2c、Es和E2s均为常数矩阵，所以L'1、L'2、L'3和L4' 均关于自变量m 连续，则g(m)的导函数关于自变量m 连续，即

由于取范数运算不影响函数的连续性，所以kX2(m)关于自变量m 的导函数是连续的，因此，kX2(m)关于自变量m 是光滑的。

2 基于CS 理论的频谱稀疏FSCS 谱图重构

对于一个有限长的信号x∈RN，假设其在某规范正交基Ψ={ψl}上是K 稀疏的(K≪N)，或称稀疏度为K，用一个与Ψ 不相关的M ×N 维观测矩阵Φ(M ＜N)对x 进行线性变换，得到观测集合y，显然观测集合y 的元素个数小于x 的元素个数，实现了对信号的压缩采样。定义降维比为η =M/N.从y 重构x 可以转化为l1范数下的最优化问题。本文采用正交匹配追踪算法(OMP)来完成［11］。

构造发射信号为频谱稀疏FSCS［10］，其脉冲串中仅有M(M ＜N)个子脉冲，子脉冲载频步进值为Li'Δf，i' =1，2，…，M，Li'为随机整数，且0 ＜Li'＜N，此外，L1=0，LM=N-1，子脉冲宽度仍为T1，脉冲重复间隔为Tr.设雷达发射第0 簇频谱稀疏FSCS 脉冲串中第i'个子脉冲信号为

式中fc+Li'Δf 为第i'个子脉冲的载波频率。当接收到相应的回波信号后，依照第1 节中的处理方法，可得到对CRRP 进行采样后的结果为

依据压缩感知理论，构造降维观测矩阵为

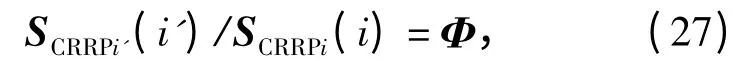
式中ΦM×N={φi'，i}为M×N 维的随机部分单位阵，

式中φ1，1=φM，N=1.

由于HRRP 可通过做关于i 的IDFT 获得，因此构造稀疏变换矩阵Ψ 为满足正交性的IDFT 矩阵。依照CS 理论，构造l1范数下的最优化问题:

这样，目标函数min ‖ΨHΦHSCRRPi'(i')‖1即为所求的HRRP，可记为^SHRRP(kX).对所有m 分别重构出HRRP，排成矩阵，即为重构的谱图(kX;m)|.

3 基于动态规划的进动特征提取方法

式中:ssn'为第n'个元素在(i;m)中对应的幅度值;ttn'为第n'个元素在(i;m)中对应的行数;uun'为第n'个元素在(i;m)中对应的列数;M'，l，ε 均为参数，满足l ＞0 且l∈2Z +1，M' ＞0 且M'∈Z，ε ＞0.具体步骤如下:

1)给定l ＞0 且l∈2Z+1，ε ＞0，M' ＞0 且M'∈Z，初始零向量ql×11，ql×12，pN'×1令计数值w = 1，w1=0.

2)令初始状态为s0=max{(i;w)}，i =1，2，…，N，此时，记imax=i，p(w)=imax.

3)令w=w+1.

4)判断，若w ＜MB，则转至步骤5);若w≥MB，则停止，令所提取到的微多普勒信息

5)i1= - (l -1)/2，q1(w1+1)=(imax+i1;w).

6)判断，若q1(w1+1)≥ε，则令q2(w1+1)=imax+ i1，i1= i1+ 1，w1= w1+ 1，转至步骤7);若q1(w1+1)＜ε，则令i1=i1+1，转至步骤7).

7)判断，若i1≤(l -1)/2，则转至步骤5);若i1＞(l-1)/2，则转至步骤8).

8)判断，若w1≤0，则p(w)= imax，转至步骤3);若w1＞0，则转至步骤9).

9)计算

10)s'0=min{G(i2)}，i2=1，2，…，l，记imax=q2(i2)，p(w)= imax，令w1= 0，ql×12= 0，转至步骤3).

4 仿真

假设高分辨雷达发射信号载频10 GHz，FSCS脉冲串内子脉冲宽度为4.882 8 ×10-7s，调频斜率4.80 ×1013，频率步进值4.687 5 MHz，每个脉冲串含有N=128 个子脉冲，合成带宽3 GHz，距离分辨率为0.05 m.假设弹头为有翼弹头［2，9］，散射点模型如图2所示。图中，散射点1～3 的坐标分别为(0，0，1)、(0.5，0.5，-0.5)和(-0.5，-0.5，-0.5).设弹头进动轴在参考坐标系中的方位角α' =60°，相对于锥旋轴仰角β' =45°，初始欧拉角φ =45°，θ =60°，φ = 90°，弹头自旋和锥旋旋转角速度均为2π rad/s，即周期均为1 s，参考点在本地坐标系的坐标为(0，0，-0.5)，积累时间2 s，FSCS 脉冲串重复频率1 kHz.传统方法获得的谱图如图3(a)所示。

图2 弹头模型在本地坐标系中表现形式Fig.2 Representation of warhead model in local coordination

当对发射信号FSCS 进行频谱稀疏处理，假设稀疏度K=4，对每个脉冲串中随机减少96 个子脉冲，M=32，获得频谱稀疏的FSCS，即降维比为0.25时，利用CS 理论重构出的谱图如图3(b)所示。CS理论重构出的谱图与传统方法获得的谱图相比可以看出，旁瓣可被有效抑制，谱图信息更加清晰。

图3 获得的谱图Fig.3 Obtained spectrum

图4(a)为利用动态规划提取到的弹道导弹进动微多普勒特征曲线，其中，l=3，ε=0.01，M' =30.可以看出，提取到的正弦曲线周期为1 000 个慢时间单元，每个慢时间单元代表1s/1 000 =10-3s，因此，计算出锥旋周期为1 s，与仿真中假设的锥旋角速度2π rad/s，即锥旋周期1 s 是一致的，这验证了(15)式的正确性;提取到的进动微多普勒曲线周期也为1 000 个慢时间单元，可计算出进动周期也为1 s，由于仿真中假设锥旋、自旋周期均为1 s，因此，计算获得的进动周期1 s 满足锥旋和自旋周期的最小公倍数，这验证了(18)式～(22)式的正确性。

图4 动态规划提取到微多普勒曲线Fig.4 Extracted micro-Doppler curve by dynamic planning

图5为频谱稀疏FSCS 降维比0.25 条件下，高斯白噪声背景中信噪比(SNR)分别为-20 dB 和-25 dB时，利用本文CS 方法重构出的弹道导弹进动微多普勒谱图，图4(b)为当信噪比为-20 dB 时，利用本文基于动态规划的提取方法提取到的弹头锥旋和进动微多普勒特征曲线信息。可以看出，本文方法具有一定的抗噪性。

5 结论

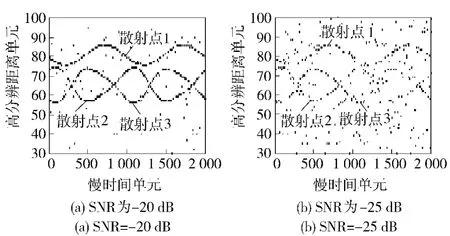
图5 降维比0.25 和不同信噪比下CS 方法重构出的谱图Fig.5 Reconstructed CS spectrum for η=0.25 and different SNRs

本文针对弹道导弹进动微多普勒信息提取问题展开研究，首先通过严格的理论推导分析了FSCS体制高分辨雷达谱图上弹头进动微多普勒特征，得到了如下结论:1)谱图上的锥旋微多普勒特征曲线仍为正弦形式，且周期为锥旋周期;2)谱图上的进动微多普勒特征曲线具有周期性，且周期为锥旋和自旋周期的最小公倍数。进一步，结合CS 理论，提出一种基于频谱稀疏FSCS 的微多普勒谱图重构方法。该方法可在大幅减少FSCS 子脉冲个数的条件下，准确重构出微多普勒谱图信息，同时，有效抑制了谱图中旁瓣的影响。在此基础上，针对CS 理论重构出的微多普勒谱图，利用弹头进动(包括锥旋)微多普勒在谱图上特征曲线的光滑性，提出一种基于动态规划的弹头进动微多普勒信息提取方法，该方法可有效提取到谱图上的弹头进动微多普勒特征曲线。

References)

［1］ Chen V C，Li F Y，Hol S-S.Micro-Doppler effect in radar:phenomenon，model and simulation study［J］.IEEE Trans on AES，2006，42(1):2 -21.

［2］ 孙照强，李宝柱，鲁耀兵.弹道中段进动目标的微多普勒研究［J］.系统工程与电子技术，2009，31(3):538 -541.SUN Zhao-qiang，LI Bao-zhu，LU Yao-bing.Research on micro-Doppler of precession targets in ballistic midcourse［J］.Systems Engineering and Electronics，2009，31(3):538 -541.(in Chinese)

［3］ 高红卫，谢良贵，文树梁，等.基于微多普勒分析的弹道导弹目标进动特性研究［J］.系统工程与电子技术，2008，30(1):50 -52.GAO Hong-wei，XIE Liang-gui，WEN Shu-liang，et al.Research on precession of ballistic missile warhead based on micro-Doppler analysis［J］.Systems Engineering and Electronics，2008，30(1):50 - 52.(in Chinese)

［4］ Zhang Y H，Zhai W S.Apply super-SVA to stepped-frequency chirp signal processing based on dechirp method［C］∥2nd Asian-Pacific Conference on Synthetic Aperture Radar.Xi'an:IEEE AESS and IEEE GRSS，2009:431 -434.

［5］ Gurbuz A C，McClellan J H，Scott W R.A compressive sensing data acquisition and imaging method for stepped frequency GPRs［J］.IEEE Trans on Signal Processing，2009，57(7):2640 -2650.

［6］ Donoho D L.Compressed sensing［J］.IEEE Trans on Information Theory，2006，52(4):1289 -1306.

［7］ 寇波，江海，刘磊，等.基于压缩感知的SAR 抑制旁瓣技术研究［J］.电子与信息学报，2010，32(12):3022 -3026.KOU Bo，JIANG Hai，LIU Lei，et al.Study of SAR side-lobe suppression based on compressed sensing［J］.Journal of Electronics ＆ Information Technology，2010，32(12):3022 -3026.(in Chinese)

［8］ 李国勇.最优控制理论与应用［M］.北京:国防工业出版社，2008.LI Guo-yong.Optimal controltheory and application［M］.Beijing:National Defense Industry Press，2008.(in Chinese)

［9］ 黄培康，殷红成，许小剑.雷达目标特性［M］.北京:电子工业出版社，2005.HUANG Pei-kang，YIN Hong-cheng，XU Xiao-jian.Radar target property［M］.Beijing:Publishing House of Electronics Industry，2005.(in Chinese)

［10］ Zhu F，Zhang Q，Lei Q，et al.Reconstruction of moving target's HRRP using sparse frequency-stepped chirp signal［J］.IEEE Sensor Journal，2011，11(10):2327 -2334.

［11］ Tropp J A，Gilbert A C.Signal recovery from random measurements via orthogonal matching pursuit［J］.IEEE Trans on Information Theory，2007，53(12):4655 -4666.