超混沌Lorenz系统的电路实现与应用

庞寿全，刘永建，朱从旭

1.玉林师范学院 物理与信息科学学院，广西 玉林537000

2.玉林师范学院 数学与信息科学学院，广西 玉林537000

3.中南大学 信息科学与工程学院，长沙410083

1 引言

混沌指在确定的非线性系统中，不需要附加任何随机因素亦可出现的类似随机行为。该现象普遍存在于自然之中，引起人们的广泛关注；混沌的理论与应用研究也已经成为非线性科学最重要的前沿内容之一。超混沌吸引子是指具有两个或两个以上的正Lyapunov 指数的混沌吸引子，其相轨较一般混沌吸引子而言，将在更多方向上分离，因而其混沌行为更为复杂。在连续的自治系统中，能够出现混沌的非线性常微分方程的最低维数为三维，而包含超混沌吸引子的相空间维数至少是四维，需要用包含4个以上的一阶耦合自治常微分方程描述，且引起系统不稳定项的数量至少为两个，常微分方程组中至少有一个非线性项[1]。 因此，超混沌系统无论在代数结构还是动力学行为上都比通常的混沌系统更复杂。

在混沌保密通信中，利用混沌信号的类随机性对有用信息进行加密，信息的保密程度与混沌模型的维数以及混沌信号的复杂程度有着直接的关系。己经证明，用简单的混沌系统加密信息并不安全[2]。因为信号一旦被截获，便可通过非线性信号的处理技术对其破译。然而高阶超混沌系统能够提供比通常混沌吸引子更为复杂的超混沌吸引子，因而具有更好的保密性[3-4]。同样的道理，正是由于超混沌吸引子的动力学行为更难以预测，使得其在需要复杂混沌行为的其他工程领域，例如数字语音、激光和振荡等各方面有着更为巨大的应用潜力和更为广泛的应用前景。因而，对超混沌的机理和应用研究成为了混沌学中的又一热点。

在维数大于4 的连续自治系统中，混沌现象是比较容易产生的。对于高维（维数大于4）连续自治系统，使其具有两个正的Lyapunov 指数也比较容易实现。常用的方法是把多个低维连续自治混沌系统耦合到一起形成超混沌系统[5]。比如，文献[6]把两个蔡式电路耦合产生超混沌；文献[7]在两个耦合的Rossler 混沌系统中实现了混沌到超混沌的转换；还有耦合振荡器产生的超混沌[8]，利用两个非线性耦合的谐振电路实现的超混沌等等。但是，能够产生超混沌的自治连续系统的最低维数是四维，因此对于四维连续自治超混沌系统的研究就具有特别的意义。据资料显示，第一个超混沌连续系统是Rossler 在1979 年利用计算机仿真获得的[9]。1986 年，Matsumoto 等人首次利用一个四阶电子电路实现了超混沌实验[10]。之后，研究人员使用不同的方法实现了一些超混沌系统，例如，利用一个四阶自治电路与一个齐纳二极管的连结来实现超混沌，利用耦合低维系统实现超混沌等。

Lorenz混沌系统作为第一个被提出的混沌系统模型[11]，已经成为了混沌系统的典范，在混沌研究领域具有广泛的普适意义。本文将在经典Lorenz 混沌系统的基础上，通过增加一个非线性控制器，构建一个新的超混沌Lorenz 系统。数值分析结果表明，非线性控制器的增加，导致新系统的动力学行为更加复杂。同时，本文还设计了与该新超混沌系统相对应的超混沌电路，通过示波器能很好地观察到该电路的混沌吸引子相图，实验结果与系统的数值模拟结果基本吻合，进一步验证了该超混沌Lorenz 系统的混沌行为。通过将新系统应用于图像加密实验，表明了由该系统产生的混沌序列具有良好的密码学特性。

2 超混沌Lorenz系统的构造

Lorenz 系统是Lorenz 于1963 年发现的首个具有混沌特性的三维自治系统，其状态方程如下：

当参数a=10,b=8/2,c=28 时，系统处于混沌状态，其吸引子在各平面的投影如图1 所示。

要使系统产生超混沌吸引子，必须满足以下条件：系统具有耗散结构，方程的维数不少于4，系统至少有两个增强不稳定因素的方程且方程中至少含有一个非线性项。当保持系统（2）参数a、b、c 与系统（1）一致时，对系统进行全微分，不难得到：

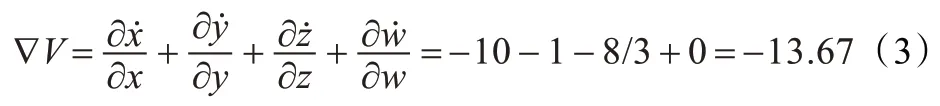
∇V ＜0，说明系统（2）满足耗散结构条件，将会产生混沌吸引子。当t →∞时，系统将以e-13.67t速率收敛，所有系统的轨线都被限制在一个体积为零的极限点集上。

3 超混沌Lorenz系统的动力学行为

为了研究系统的动力学行为随控制参数k 的变化情况，保持参数a、b、c 的值与系统（1）一致，令k 在（0，17）区间变化，得到系统随k 变化的分岔图，如图2 所示。 Xmax表示系统在每个不稳定周期或稳定周期中x 的峰值，当系统做周期运动时，对应同一个k 值Xmax只能取到一个或有限几个值，而当系统处于混沌状态时，对于同一个k 值Xmax却能取无数个值。同时还不难得到系统的Lyapunov 指数随k的变化图，如图3 所示。

由图3 可以看出，当k ∈(0,3.8)，系统的4 个李雅普诺夫指数λ1＞0, λ2＞0, λ3=0, λ4＜0，说明此时系统处于超混沌状态。当k ∈(3.9,6.2)时，λ1=0, λ2=0, λ3＜0, λ4＜0 ，系统处于拟周期运动状态；当k ∈(6.3,10),λ1＞0,λ2=0,λ3＜0,λ4＜0，系统又处于混沌状态，当k ∈(10,11)系统的第一个李雅普诺夫指数λ1出现多次正负变化，说明系统处于周期和混沌两者之间交替变化的状态。 k ∈(11.2,12)时，第一个李雅普诺夫指数λ1恒为正，则说明系统保持混沌状态不变，当k ＞12 时，λ1=0，系统运动状态为周期振荡。当参数k=2 时，λ1=0.223 0, λ2=0.138 9, λ3=0, λ4=-14.038 0, 由此可得系统吸引子的分形维数：

图2 系统（2）随参数k变化的分岔图

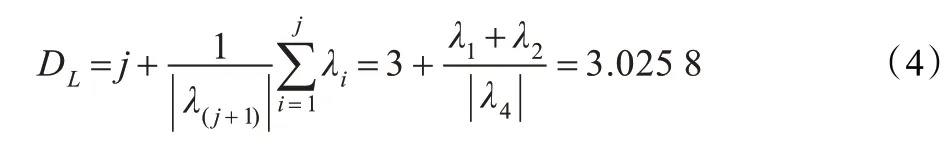
DL为分数，表明系统具有分形特征。

由以上分析可知，随着控制参数k 的变化，系统（2）将呈现出不同的动力学行为。利用Matlab 软件，采用四阶龙格-库塔算法，对系统进行了数值模拟，得到系统（2）的混沌吸引子相图分别如图4 和图5 所示。由图4 可见，随着k 的变化，得到了系统分别处于超混沌、拟周期、混沌和周期的运动状态。图5 为系统混沌吸引子在各个平面的投影图。

彭加莱截面也是系统动力学行为特征的重要判据，但截面的选取必须恰当，截面不能和吸引子的轨线相切，也不能在轨线平面上。当彭加莱截面是两个离散的点时，说明系统是周期振荡，截面上出现几对离散点，系统运动形式是拟周期振荡。当系统的彭加莱截面是由片状或线状的、并具有分形特征的大量点组成时，系统的运动方式是混沌运动。为了进一步判断系统的动力学特征，根据系统混沌吸引子截取得到系统（2）的彭加莱截面图，如图6 所示，可见系统具有混沌行为。

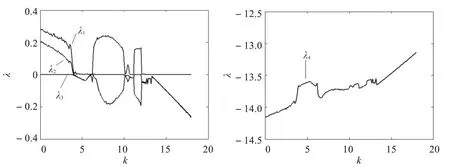
图3 Lyapunov 指数随参数k变化

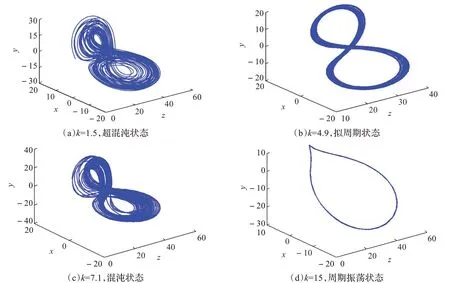
图4 控制参数k取不同值时，系统混沌吸引子呈现的状态特征

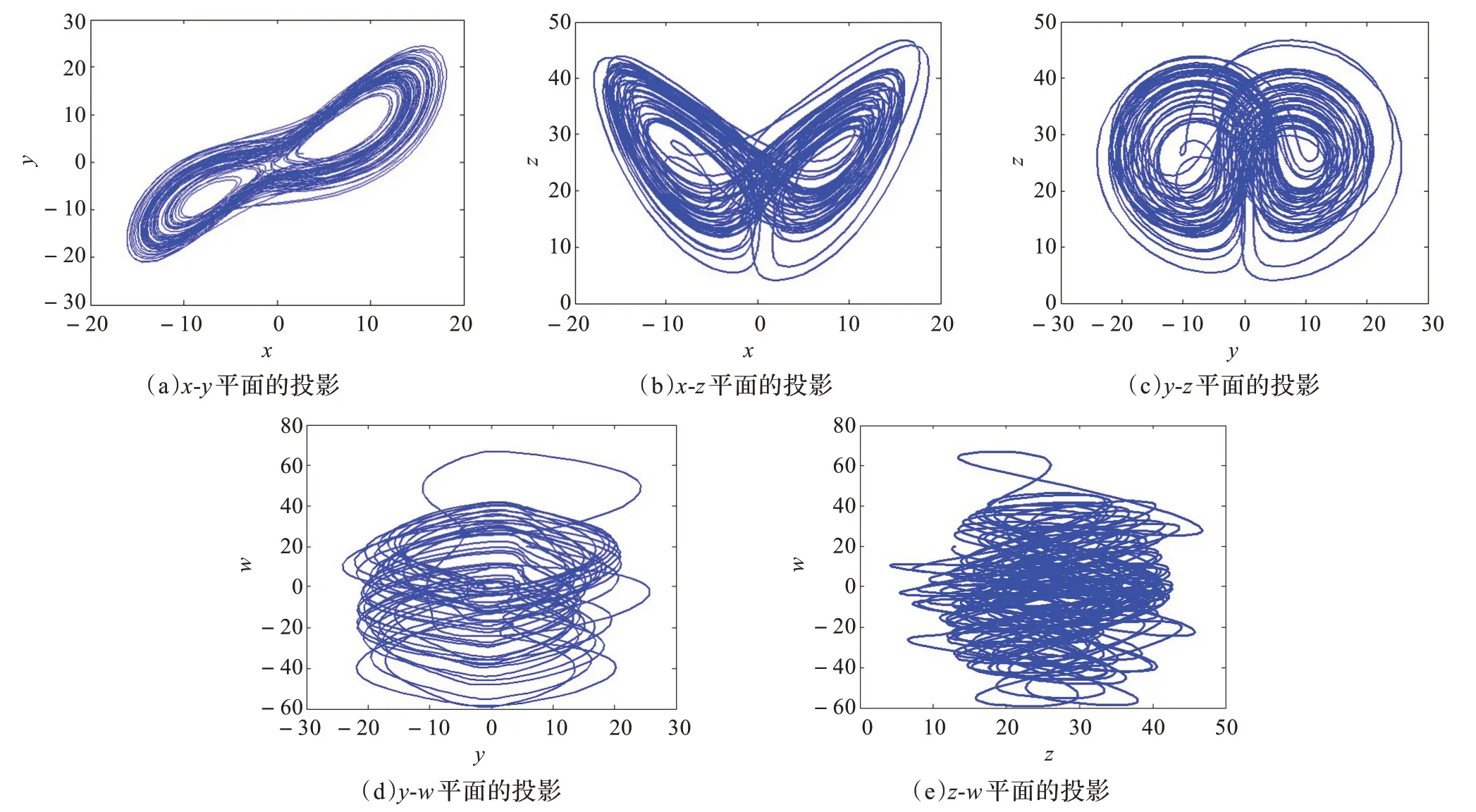
图5 k=1.5 时系统吸引子在各平面的投影图

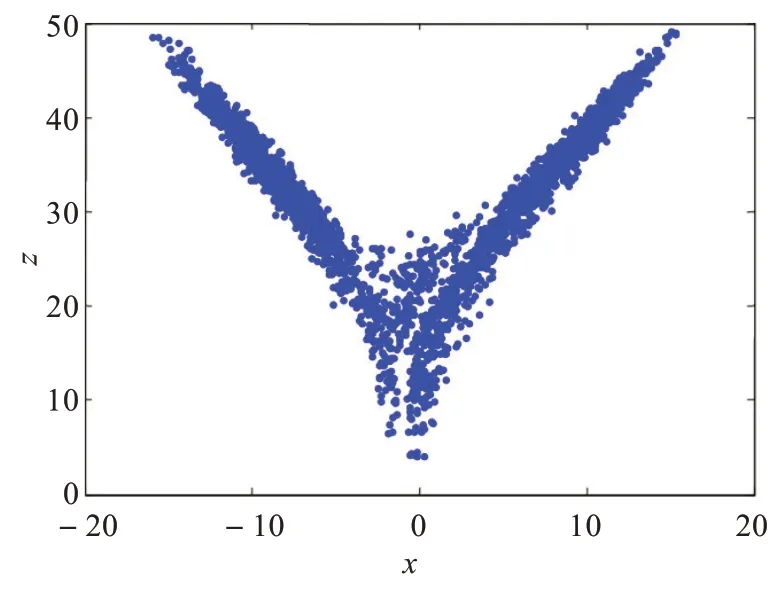
图6 系统（2）在x-z平面上的彭加莱截面图

4 超系统Lorenz系统电路的设计及其实验

为了从实验上验证混沌系统的动力学行为，可以采用设计非线性电路的方法，用电压来模拟系统的状态变量，这种实验方法的物理量易于测量，同时也能较准确地反映混沌系统的动力学行为[12]。为了验证系统（2）的动力学行为，根据系统（2）的数学模型，设计了一个非线性实验电路，以便于观察系统的动力学行为。在设计电路的时，为了能更好地观察系统的状态变化图，在不改变系统状态性质的基础上，对系统方程进行线性变换，以便于使系统的变量在电路元器件允许的范围内变化。于是将系统（2）的方程进行线性变换成如下形式：

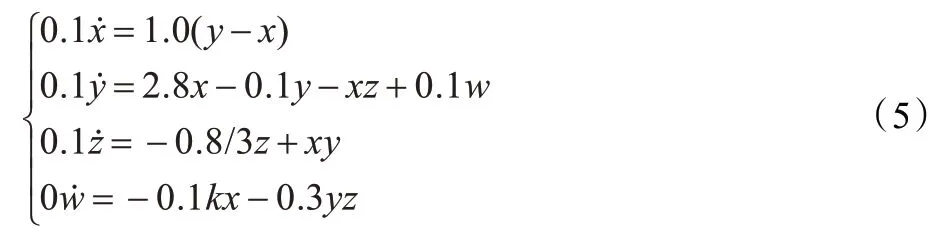
根据上述方程（5），不难设计出如图7 所示的电路和电路方程（6），根据实验设计电路再给出实物图。图中U1～U11采用型号为LM741 的运算放大器，模拟乘法器采用了AD633 型号。

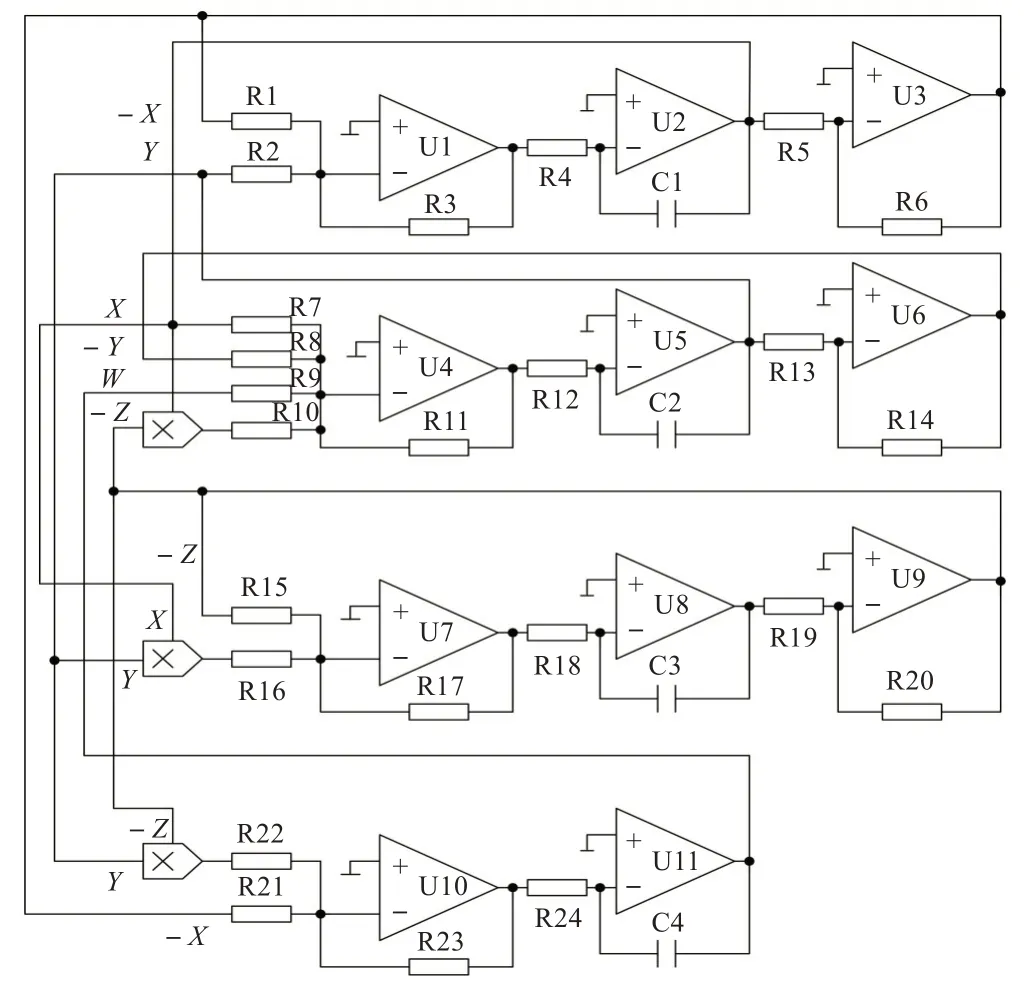
图7 超混沌Lorenz系统的电路实现图

该电路的电路方程为：

该电路方程与系统（2）的方程形式是一致的，通过选用合适的元件参数，即可以实现与系统（2）一致。因此，取R1=R2=R3/1.0, R7=R11/2.8, R8=R9=R11/0.1, R10=R11/10 ，R15=R17/2.8,R16=R17/10,R22=R23/3，通过改变R21来实现对参数k 值的改变。同时取R3=R4=R5=R6=R11=R12=R13=R14=R17=R18=R19=R20=R23=R24=10 kΩ,则R1=R2=10 kΩ,R7=3.57 kΩ,R8=100 kΩ,R9=100 kΩ,R10=1 kΩ,R15=3.75 kΩ,R16=1 kΩ,R22=300 kΩ,R23=50 kΩ。另外，为了便于能在示波器上观察到完整、稳定的波形图，取C1=C2=C3=C4=100 nF,此时波形的振荡频率约为1 000 Hz，通过示波器观察到的实验结果如图8 所示。由图可见，电路的实验结果和系统（2）的数值仿真结果吻合。

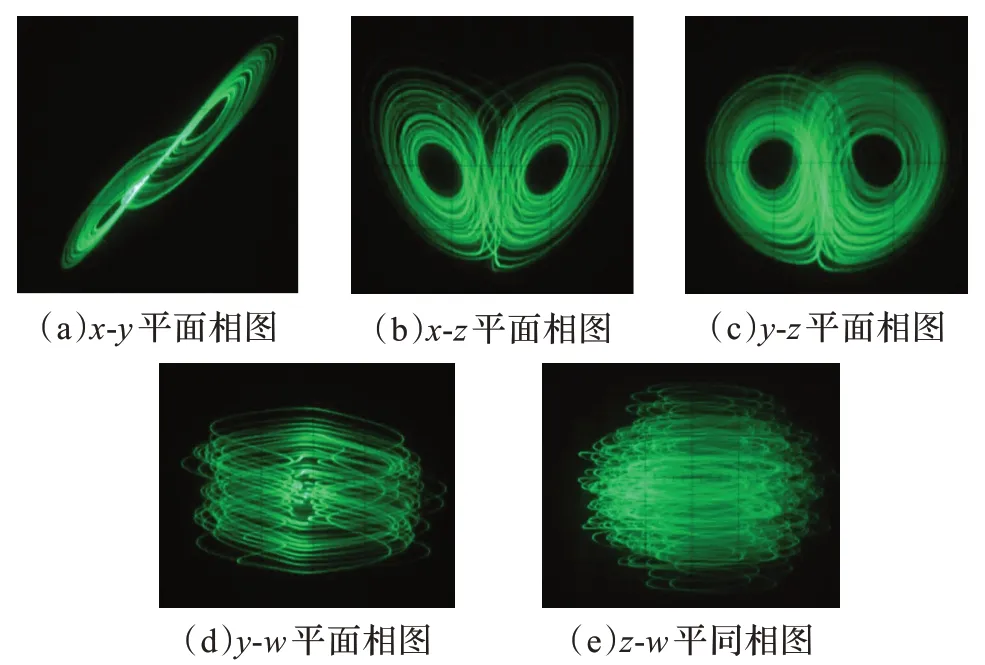
图8 实验电路在示波器中演示得到的实验结果

5 新系统在图像加密中的应用

将本文提出的超混沌Lorenz 系统（2）应用于图像加密，实验取256×256×8 位的标准Lena 灰度图像（像素数量N=256×256）。系统（2）的状态初值取（2.4，3.5，4.6，5.0）；系统参数取：a=10，b=8/3，c=28，k=2.0，使得系统（2）是超混沌的；时间步长取0.001。预迭代1 000 次后，继续迭代N/4次，对4 个状态变量序列各取后面长为N/4 的子序列，再将4 个子序列连接成长度为N 的序列S={xi,yi,zi,wi,i=1,2,…,N/4}, 令S={sj},j=1,2,…,N 。然后按公式（7）对序列S 进行改造（即取sj实数的小数点后14 位数字构成的整数对256 取余），得到适用于图像加密的密钥序列K={kj},j=1,2,…,N 。

其中，floor（x）取小于或等于x 的最大整数。然后，利用公式（8）明文图像像素pi逐个进行加密，得到密文像素序列{cj}：

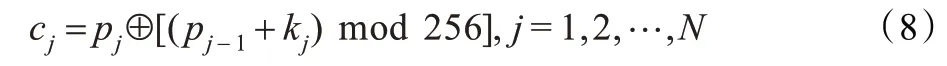
其中，p-1为一预设常数，这里取p-1＝66。实验所得结果如图9 所示，图（a）和（b）分别是原始图像及其像素值分布直方图，而图（c）和（d）则分别是加密图像及其像素值分布直方图。

图9 Lena图像加密实验结果

从图9 可以看到，加密图像的直方图呈非常均匀的分布，完全不同于原始图像的直方图，这表明由超混沌系统（2）产生的混沌序列所加密的图像，其像素值分布是均匀的。因此，密文将具有很好的抗统计分析攻击的性能。

6 结论

本文在经典的Lorenz 系统的基础上，通过引入非线性控制器，构建了一个新的四维超混沌系统，通过调整新系统的控制参数，实现了系统的超混沌、混沌、拟周期和周期振荡等丰富的动力学行为。此外，根据新的超混沌Lorenz系统方程，设计了实验电路，通过电路状态量的测量进一步验证了该Lorenz 系统的动力学行为及其演化规律，电路的实验结果与数值仿真的结果能很好地吻合。本文的理论及电路设计方法，对超混沌信号源的设计均具有指导意义。最后，将该系统应用于图像加密实验，结果表明，该系统产生的伪随机序列具有很好的密码学性能，因此，该系统在多媒体信息保密通信和信息安全领域具有良好的应用前景。

[1] 刘崇新.一个超混沌系统及其分数阶电路仿真实验[J].物理学报，2007，56（12）：6865-6873.

[2] Periz G，Cerdeira H A.Extraeting messages masked by chaos[J].Physical Review Letters，1995，74：1970-1973.

[3] Boutayeb M，Darouach M，Rafaralahy H.Generalized state-space observers for chaotic synchronization and secure communication[J].IEEE Transactions on Circuits and Systems I：Fundamental Theory and Applications，2002，49（3）：345-349.

[4] 孙琳，姜德平.驱动函数切换调制实现超混沌数字保密通信[J].物理学报，2006（7）：3283-3288.

[5] Pang Shouquan，Liu Yongjian.A new hyperchaotic system from the Lü system and its control[J].Journal of Computational and Applied Mathematics，2011，235（8）：2775-2789.

[6] Kapitaniak T，Chua L O，Zhong G Q.Experimental hyperchaos in coupled Chua’s circuits[J].IEEE Transactions on Circuits and Systems I：Fundamental Theory and Applications，1994，41（7）：499-503.

[7] Nikolov S，Clodong S.Hyperchaos-chaos-hyperchaos transition in modified Rössler systems[J].Chaos，Solitons and Fractals，2006，28（1）：252-263.

[8] Grygiel K，Szlachetka P.Chaos and hyperchaos in coupled Kerr oscillators[J].Optics Communications，2000，177（1/6）：425-431.

[9] Rosler O E.An equation for hyperchaos[J].Physics Letters A，1979，71（2/3）：155-157.

[10] Matsumoto T，Chua L O，Kobayashi K.Hyperchaos：laboratoryex periment and numerieal confirmation[J].IEEE Transactions on Circuits and Systems I：Fundamental Theory and Applications，1986，33：1143-1147.

[11] Lorenz E N.Deterministic non-periodic flows[J].Journal of the Atmospheric Sciences，1963，20：130-141.

[12] 黄丽莲，辛方，王霖郁.新分数阶超混沌系统的研究与控制及其电路实现[J].物理学报，2011，60（1）：77-85.