一种新型跟踪离散1/f噪声信号递归RLS 算法

曹昌勇

皖西学院 机械与电子工程学院，安徽 六安237012

1 引言

1/f 噪声是一种普遍存在于物理、生物、社会、医学、天文、地理等系统中的自然现象，1925年约翰逊（Johnson）在电子管中首次观察到1/f噪声。在以后的研究中，1/f噪声一直是电子元器件和电子线路低频噪声的主要形式[1]。20 世纪80 年代以来的研究发现，电子元器件中的1/f噪声的大小与电路的可靠性有密切的关系。一个1/f 噪声很大的元器件或电路，很可能存在较严重的可靠性问题，其寿命则会较短，而且抗恶劣环境的能力也就较差。因此，人们通过检测和分析电子系统1/f噪声的性质，就可以间接地预测电路或系统的质量和可靠性[1-2]。自从发现1/f 噪声的近百年时间里，人们对它的产生机理进行了大量的研究，提出了各种不同的模型，但仍然还没有一个统一的理论。人们发现1/f 噪声与系统的缺陷有关，是一个复杂的动力系统[3]，满足长期统计规律，并且是长程相关的。对如何生成1/f噪声的研究，也有不少的模型，比如分数阶布朗运动过程（fBm）；通过混沌模型[4]来生成1/f 噪声，该方法用一个logistic 混沌序列输入到hosking 分数阶差分滤波器中，并能产生具有混沌特性的1/f噪声序列；通过小波变换[5]，该方法根据白噪声的小波变换后的系数仍服从白噪声规律，然后正交归一化小波系数找到满足1/f信号生成定理的正交小波系数集，通过Karhunen-Loeve 展开式生成1/f 信号。对1/f 噪声的参数估计，主要采用的办法有小波变换、最小二乘、时频分析等；对于跟踪1/f噪声，普遍采用自适应算法，比如最小均方误差（LMS）算法，文献[6]提出了一种变步长LMS 算法跟踪fBm 过程。由于LMS 算法收敛速度慢，因此本文采用改进的最小递归二乘法（RLS）来跟踪1/f噪声，但是这种算法存在计算复杂，迭代步数增加到一定程度滤波器系数必定发散等缺点。

自适应算法被广泛应用在系统辨识、预测建模、噪声对消以及信道估计等领域。它与滤波器一起构成自适应滤波器，可以在一定程度上对噪声进行过滤，基本原理如图1 所示。

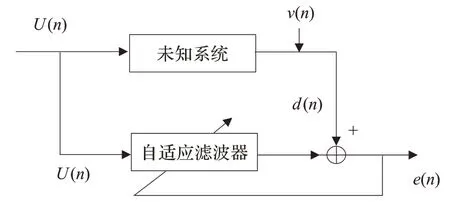
图1 自适应滤波器原理图

自适应算法有很多，用的最多的要数LMS 和RLS 算法。为了更好地对非平稳信号进行处理，需要对算法进行改进。人们在改进这两种算法的过程中做了大量的工作。对LMS 算法的改进一般采用的办法是变步长[6-7]，或者是考虑引入梯度算法[8]或其他算法实现对快速变化的信号进行跟踪。对于RLS 算法来说，它的收敛速度比LMS 要快得多，但它是以增加计算量为代价的。影响计算复杂度的关键在于该滤波器算法的结构上。文献[9]提出了一种分级实现的RLS 算法，它把大的滤波器阶数分解成几个级联的阶数小的滤波器；文献[10]通过输入滤波器的信号的自相关函数是服从递归规律建立了扩展算法（ERLS）；文献[11-12]通过误差反馈的办法，在文献[9]的基础上增加一个误差判断开关，通过开关切换去修改变化比较大的级联滤波器的系数，达到部分更新滤波器系数的效果，进而减少运算量。对RLS 算法的收敛速度上的改进主要是实时修正RLS 算法的记忆因子[13]。对于非平稳信号来说，主要是期望能快速根据输入信号的变化来调整滤波器系数。

正规或者快速RLS 算法是建立在迭代计算基础上的，因此在有限的计算机精度的条件下，必定要发散。为了解决滤波器权系数发散的问题以及快速准确的跟踪信号变化的问题，本文根据输入滤波器的信号的自相关矩阵应该满足慢变化的规律，引入误差的非线性函数来控制这个变化以实现实时快速跟踪1/f信号。该算法继承了正规RLS算法的快收敛特性，并且不增加正规的RLS 算法的计算量，误差也比正规RLS 算法有所减小。通过该方法对混沌1/f噪声过程与fBm 过程进行跟踪仿真，实验表明它具有良好的稳定性，算法收敛速度较正规RLS 算法没有降低，在小的滤波器阶数的条件下也具有良好的跟踪能力。该算法在遇到突变输入时会快速调整滤波器系数，因此在短时间内滤波器系数的改变比正规RLS 算法要快得多，这就实现了快速跟踪目标，从而减小了误差。

RLS 算法中记忆因子对算法的跟踪速度有比较大的影响。当记忆因子比较小时，算法响应快变信号的能力强，但抗干扰能力弱，适合于跟踪非平稳信号；当记忆因子较大时，算法响应快变信号能力比较差，但抗干扰能力强，适合跟踪平稳信号。记忆因子的大小与抗干扰强弱是矛盾的。因此记忆因子的调整量太大和太小都不好，本文给出了记忆因子与输入信号自相关矩阵的特征值（fBm 噪声信号）的一个表达式，为动态调整记忆因子提供了理论依据。

2 1/f噪声的两个模型

所谓1/f过程是指随机过程x（t）的功率谱是幂函数的形式，即S(f)=σ2/f a，其中σ2是常数，由于其产生机理不明，一般都把它当做是一种随机过程，它在低频部分的功率特别大，特别是频率靠近0 的时刻。

2.1 1/f混沌模型

文献[4]通过采用logistic 方程生成混沌序列，然后把混沌序列输入到hosking 分数阶滤波器，表示如下。

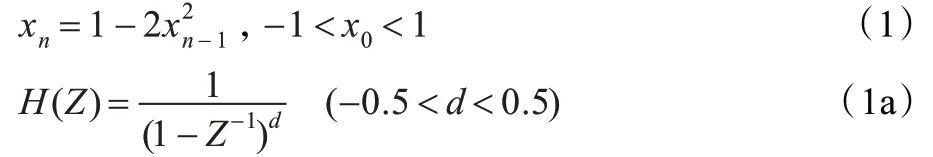
其中，H(Z)为hosking 分数阶滤波器的传递函数，其冲击响应为：

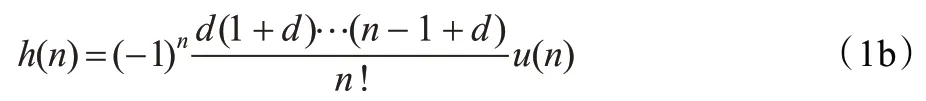
其中，u(n)是单位阶跃函数，式（1b）的离散递推表达为：

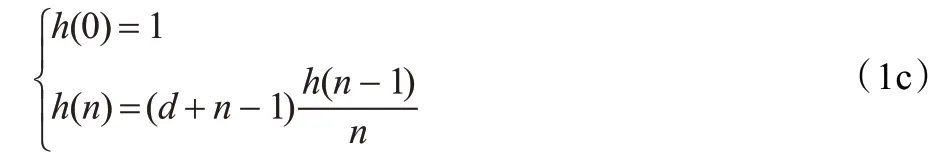
通过求式（1）与式（1c）的卷积即可得到混沌1/f噪声信号。式（1）产生的混沌序列的均值为0，自相关函数与白噪声的自相关函数相似。

2.2 分数维布朗运动过程

文献[6]提出了一种变步长的LMS 算法跟踪fBm 过程。如果一个时间连续的随机过程的统计特性是尺度不变的就叫自相似过程，自相似可用公式表示如下：

z(t)即为一个具有自相似指数H（Hurst 指数）的自相似随机过程，它对任意的标量c＞0 都具有自相似性。式（2）中的不等号仅仅在统计意义上对所有有限分布满足自相似性。具有平稳增加的非平稳的，且具有自相似性的高斯随机过程就是分数维布朗运动过程，计为BH(t)，一个fBm 过程的一阶导数称为分数维高斯噪声（fGn）。离散的fBm 可表示如下：

Ts为采样周期，因为分数维布朗运动具有自相似性，不失一般性，取Ts=1。离散fBm 的均值、方差与自相关函数表示如下：

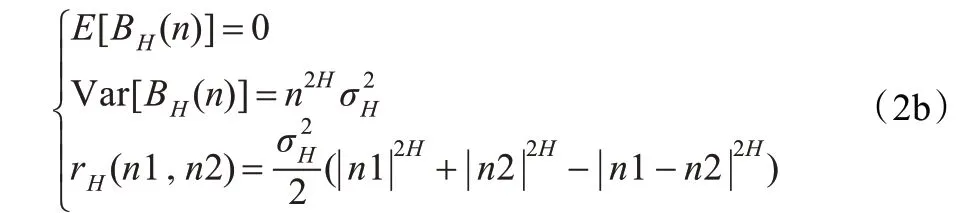
引理1 Hurst 指数为0 ＜H ＜1 的离散第一阶分数维布朗运动（1-fBm）的自相关函数R(n)（M×M 阶矩阵）能被对角化为R(n)=QΛ(n)QT，如果它的近似估计在n 比较大时成立，这里Q(n)≈Q 是一个常数正交矩阵，Λ(n)=diag{λ1,λ2,…,λM-1,λM(n)}。 R(n)的前面M-1个特征值是与时间无关的，特征值λM(n)是时间n 的函数。所有特征值都与Hurst指数H 相关，指数H 刻画了离散分数维布朗运动，具体见公式（2a）。其最大的特征值是时间n 和Hurst指数H 的函数。该特征值可用下式表示：

3 RLS 算法及修正

3.1 基本RLS 算法

假如滤波器阶数为M，n 时刻的权系数为W(n)=[W1(n),W2(n),…,WM(n)]T，输入数据为向量U(n)=[u(n),u(n-1),…,u(n-M+1)]T，则输出设为y(n)其表达如下：

期望输出为d(n)，表达如下：

其中W0为最优滤波器系数，假设η(n)是均值为0，方差为的高斯白噪声，文献[14]考虑了η(n)服从独立同分布的噪声，采用类A 噪声模型进行分析，本文仅考虑高斯白噪声的情况。n 时刻的估计误差为：

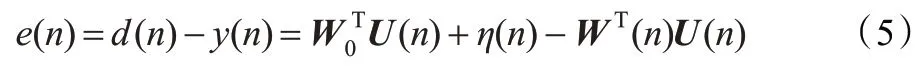
基于最小二乘法的RLS 算法的最小化代价函数如下：

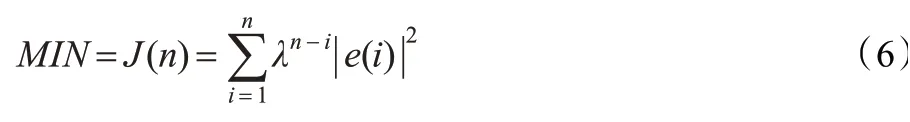
λ 为递归最小二乘算法的记忆因子，满足0 ＜λ ＜1，它对当前的误差记忆强，对过去时刻的误差记忆弱。把式（5）代入式（6）并两边对W 求导数，令其导数为0，即

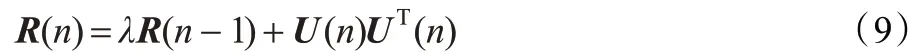
对式（9）利用矩阵求逆引理可得到其逆矩阵的递推表达式：

令P(n)=R-1(n)为输入信号的自相关矩阵的逆矩阵：

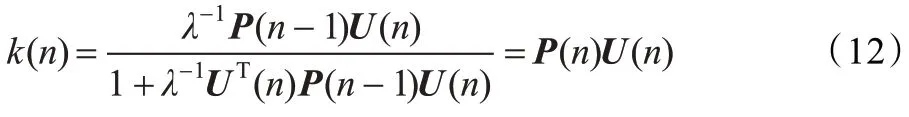
将式（11）与式（12）代入到式（8）得到权系数的递推公式（13b）：

上面的四个表达式给出了常规的RLS 算法的一个迭代表达，要满足迭代，需要初始化的项为P(n)和W(n)。一般W(0)初始化为长度为M 的0 向量，P(0)=δ-1IM，IM为M 阶的单位矩阵，δ 当输入信号的信噪比大时取小的正数，反之取大的正常数[15]。

在式（12）中，P(n)是输入向量的时间平均相关阵的逆矩阵。

3.2 修正RLS 算法

本文对式（13c）P(n)进行修正，用一个非线性的误差函数来修正它，并用式（15a）取代式（13c）。

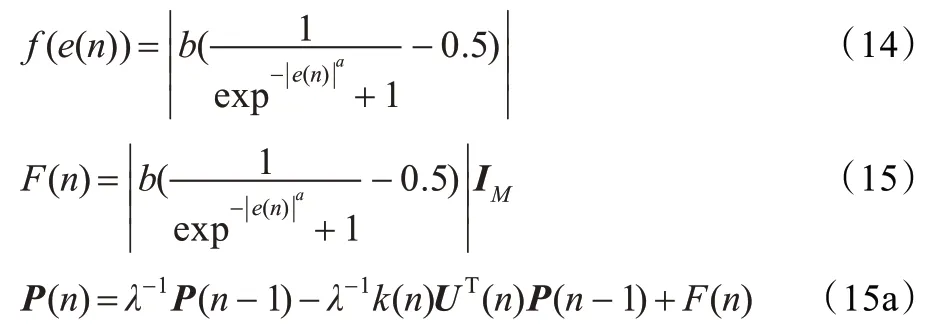
公式（14）所对应的关系曲线如图2 所示，其中a 取0.8，b 取3，可以根据程序设置不同的值来讨论曲线的变化情况；公式（15）不需要赘画，因为IM是一个单位矩阵。 f(e(n))是关于误差e(n)的非负非线性函数，把绝对值与a 去掉即为参考文献[3]中函数的形式。式（14）中的a 与b 是正数，一般与被跟踪的信号有关，可以通过图2 曲线图讨论来确定。误差一般不为0，当误差增大时P(n)增大，即表示信号在快速变化，信号发生了突然的变化，这需要在下一次比较大的调整权系数W(n)，通过观察式（13），由于P(n)增加，导致k(n)增加比较大，从而W(n)得到了大的调整，说明信号是快变的；相反，当误差很小时，表示滤波器权系数不需要进行大的调整，从式（14）可见小的误差不会对原来的P(n) 产生大的改变，因此k(n) 的变化也比较小，从而W(n)的调整很小，这表明输入信号在这一小段时间内是平稳的。另一方面，由于P(n)的改变，可以说是对它进行了一个变化的初始化工作。

图2 F（n）同e（n）的关系曲线

对于RLS 算法，P(n)是集平均输入向量自相关阵R(n)在n 时刻的逆矩阵，在正规的RLS 算法中，该项是一直迭代下去的，由于计算机精度问题，必定会导致P(n)不可逆，导致R(n)的特征值发生突变。特征值发生突变的根本原因是有部分非平稳数据的输入，造成误差增大，导致权系数调整过大，最终算法发散。因此一种办法是通过关于误差的非线性函数来修正权系数的调整[14]，即非线性RLS 算法。本文用非线性函数来微量调整P(n)矩阵，这样可以避免特征值的突变，但算法仍然是线性的RLS 算法。

3.3 与λ 相关的一个表达式

下面推导记忆因子λ 与输入信号（1-fBm）的自相关矩阵的特征值的一个重要关系。

把式（4）、式（16）代入式（13a）得到：

由式（12）、式（13b）、式（16）和（17）推出：

对式（18）两边分别取期望得到：

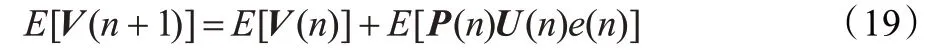
根据P(n)满足慢变规律，可知它相对于输入U(n)与误差e(n)来说，它的变化显得很小，因此可以把它看做是与输入和误差相互独立的，故可表达如下：

由式（16）和式（13b）知，V(n)与U(n)独立，假设观测噪声η(n)与U(n)相互统计独立，且η(n)的均值为0，将式（17）代入到式（20）得到：

其中，RU(n)=E[U(n)UT(n)]为n 时刻输入滤波器数据的自相关函数，在式（21）中，根据式（12）得到，且RLS 算法需要初始化P(0)=δ-1IM，即R(0)=δIM，故：

把式（22）、式（23）代入式（21），并考虑到输入数据的自相关矩阵是缓变的，把当前时刻自相关阵与之前时刻的相关阵看做是可以近似统一的（记忆因子的存在也为这种近似统一提供了依据），因此得到：

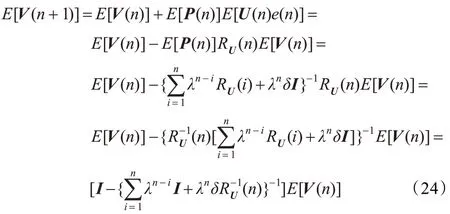
由引理1 可知，式（24）RU(n)=QΛ(n)QT，其中Q 为正交的矩阵，Λ(n)是由RU(n)的特征值构成的对角阵，设其特征值为λ1,λ2,…,λM-1,λM(n)，其中λM(n)在式（2c）中给出。因此式（24）转化为：

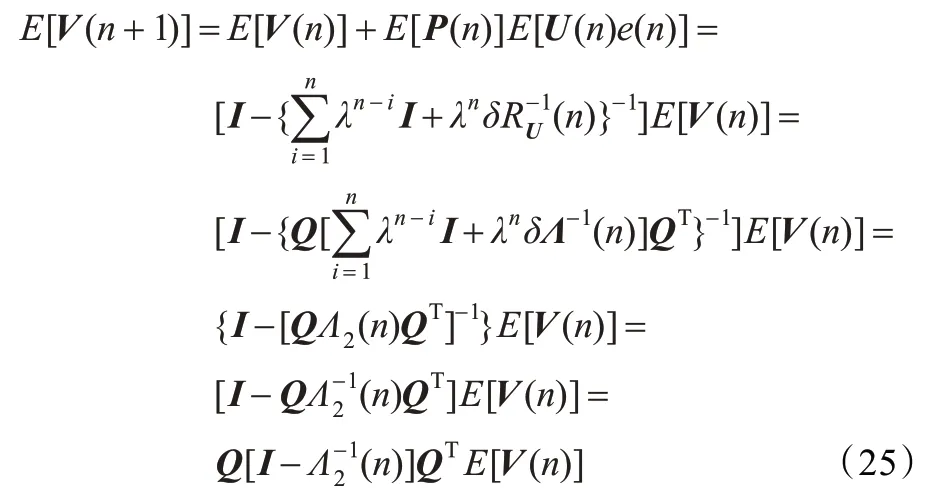
设B=I-Λ2(n)-1，由于，因此B 的特征值可以用Λ(n)的特征值来表示。式（26）给出了一个迭代过程。RLS 算法收敛意味着当n 趋于无穷时：

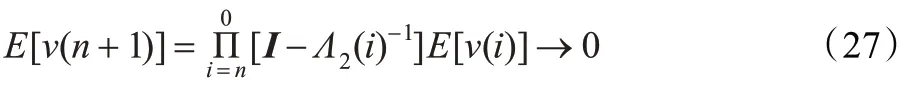
即当n 趋于无穷时，W(n+1)→W0达到最优值。

其中λΛ2(j,i)为Λ2在第i 次迭代过程中第j 个特征值。由可以把Λ2表示出来：

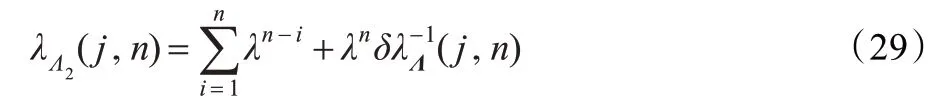
最后由式（28）得到收敛的条件为：

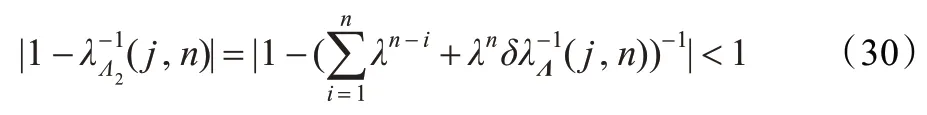
公式（30）给出了记忆因子λ 与输入信号的自相关矩阵的特征值λΛ(j,n)在n 时刻的一个表达式，这为在跟踪过程中动态调整RLS 算法的记忆因子λ 给出了理论上的依据。

公式（30）说明调整过程中算法的记忆因子是受到自相关矩阵的特征值λΛ(j,n)控制的。该公式是记忆因子满足的一个关系表达式，可以根据这个公式来设置记忆因子，当然，如果记忆因子在每次迭代过程中的设置不满足这个条件时，算法肯定会发散，从这个角度看，属于收敛条件范畴的讨论。

4 仿真结果

4.1 对混沌1/f信号跟踪的仿真

根据第2章中的第一个模型产生1/f时间序列（初始值取0.3，hosking 分数阶滤波器d=0.4），取3 000 个离散数据。设修正的RLS 算法滤波器阶数为M=10，观测噪声方差为0.4，得到如图3 的跟踪结果（误差均值与方差分别为0.046 5、0.467 4）。

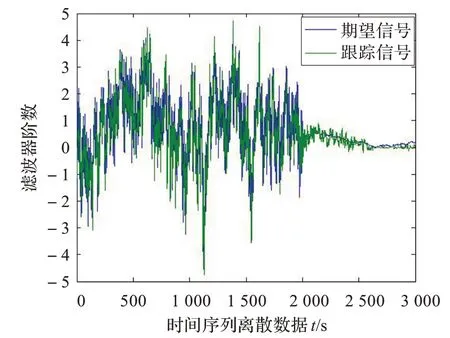
图3 修正RLS 算法对混沌1/f噪声序列的跟踪（a=5，b=0.005）

标准RLS 算法的跟踪结果如图4 所示（误差均值为0.047 7，方差为0.480 4）。

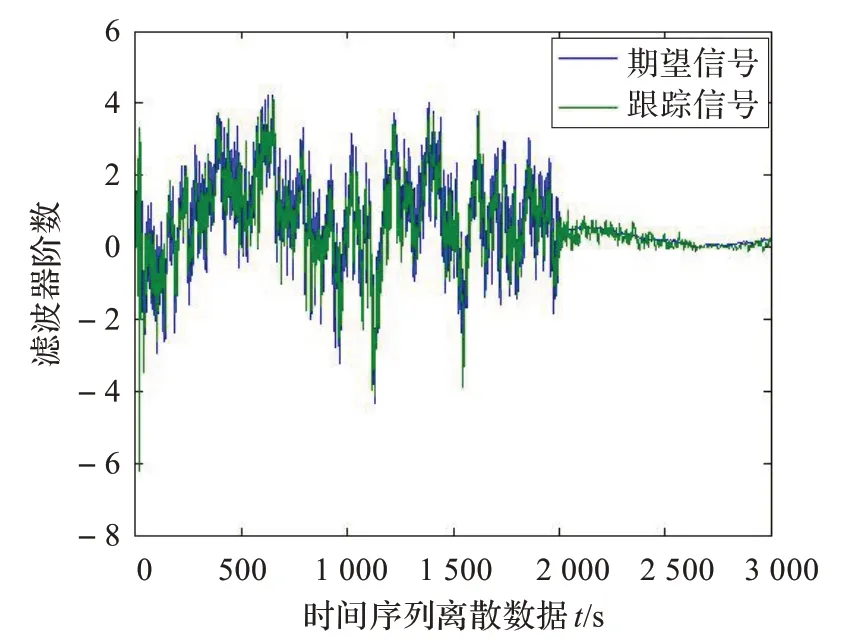
图4 标准RLS 算法跟踪混沌1/f噪声信号

从对混沌1/f噪声信号的跟踪情况看，修正RLS 算法比标准RLS 算法弱占优势，其均值和方差均比标准算法小。

4.2 对1-fBm 噪声信号的跟踪

取H=0.7，滤波器阶数为10，修正算法与标准算法结果如图5（误差均值与方差分别为0.001 7、0.104 0）和图6 所示（均值为-0.005 6，方差为0.274 2）。

图5 修正RLS 算法对混沌1/f噪声序列的跟踪（a=5，b=0.5）

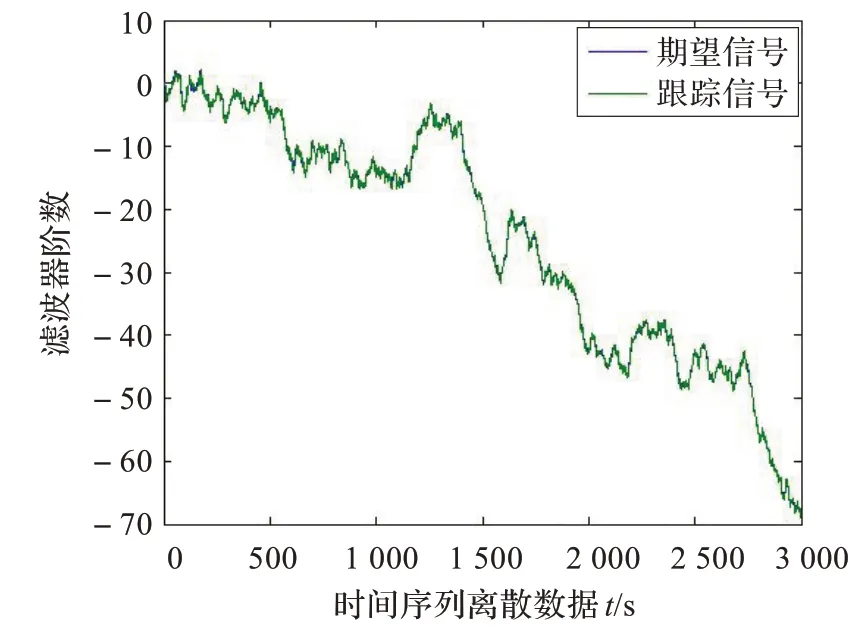
图6 标准算法跟踪1-fBm 信号

从对混沌1/f 信号或1-fBm 的结果看，修正的算法比标准算法要好。从图7 与图8 在对跟踪1-fBm 过程中滤波器系数的调整过程可以看出，修正算法滤波器的系数可以发生快速改变，而标准算法只是很慢地变化，这也导致它的误差比较大，跟踪速度达不到的原因。

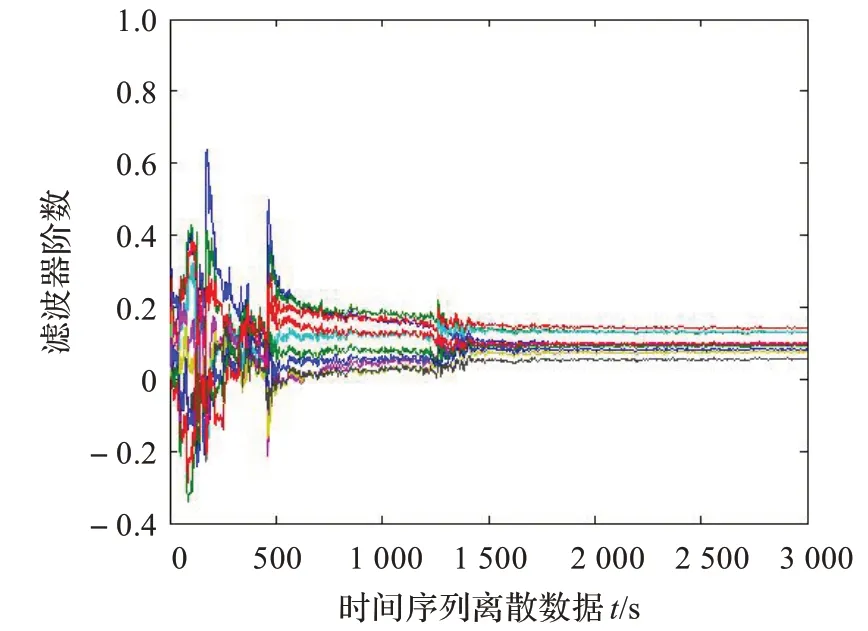
图7 修正算法对滤波器系数的调整过程

图8 标准RLS 算法对滤波器系数的调整过程

图7、图8 中不同的颜色曲线表示的是RLS 算法中各个滤波器系数的动态曲线，由于滤波器系数一般都不止一个，因此为了区别每一个系数的动态变化，作图时采用了不同的颜色。

从图7 可见，迭代时会出现滤波器系数的调整过程；对比图8 的系数调整可见，算法不会影响收敛速度。

5 结束语

RLS 算法是一种快速收敛的算法，但是在跟踪非平稳信号时无法快速调整滤波器系数以便实时跟踪，并且在迭代次数达到很大时算法必将发散，本文通过引入一个非线性函数来对输入信号相关逆矩阵进行修正，这样可以快速调整滤波器系数，以适应信号的快速变化。对两个1/f噪声模型产生的序列进行仿真实验，结果表明修正方法比正规的RLS 算法要好。此外，本文还推导了RLS 算法的记忆因子与输入信号自相关矩阵特征值的一个关系，这为动态调整记忆因子提供了理论上的依据。

[1] 庄奕琪，马中发，杜磊.1/f 噪声之谜[J].世界科技研究与发展，1999，21（4）：69-72.

[2] 杨冬云，王司.1/f 分形噪声理论及其在信号处理中的应用研究综述[J].黑龙江工程学院学报：自然科学版，2004（3）：31-35.

[3] 许生龙.1/f噪声的动力学统计理论[J].红外技术，2003（5）：63-67.

[4] 张强，马润年，许进.1/f过程的混沌模型[J].信号处理，2001（5）：392-394.

[5] 李光，于盛林.基于小波变换的拟1/f 信号生成[J].数据采集与处理，2003（1）：119-122.

[6] Gupta A，Joshi S D.A novel least mean squares algorithm for tracking a discrete-time fBm process[C]//Proceedings of 2006 Annual India Conference，2006.

[7] 覃景繁，欧阳景正.一种新的变步长LMS 自应用滤波算法[J].数据采集与处理，1997（3）：171-174.

[8] Ang W P，Farhang-Boroujeny B.A new class of gradient adaptive step-size LMS algorithms[J].IEEE Trans on Signal Processing，2001，49：805-809.

[9] Wu An-Yeu，Liu K J R.Split recursive least-squares-algorithms，architectures，and applications[J].IEEE Trans on Circuits and Systems Part II：Analog and Digital Signal Processing，1996，43：645-658.

[10] Haykin S，Sayed A H，Zeidler J R，et al.Adaptive tracking of linear time-variant systems by extended RLS algorithms[J].IEEE Transactions on Signal Processing，1997，45（5）.

[11] Jin Minglia.Partial updating RLS algorithm[C]//Proceedings of the 7th International Conference on Signal Processing（ICSP’04），Beijing，China，2004：392-395.

[12] Niu Wei，Wang Minxi，Chen Kaya.A novel reduced order RLS predistortion[C]//Proceedings of Microwave Conference，Asia-Pacific，2005.

[13] Park D，Jun B E，Kim J H.Fast tracking RLS algorithm using novel variable forgetting factor with unity zone[J].Electronics Letters，1991，27：2150-2151.

[14] Weng J F，Leung S H.Nonlinear RLS algorithm for amplitude estimation in class A noise[J].IEEE Proceedings Communications，2000，147：81-86.

[15] Wei P C，Han Jun，Zeidler J R，et al.Comparative tracking performance of the LMS and RLS algorithms for chirped narrowband signal recovery[J].IEEE Transactions on Signal Processing，2002，50：1602-1609.

[16] Chun B，Kim B，Lee Y H.Generalization of exponentially weighted RLS algorithm based on a state-space model[C]//Proceedings of the IEEE International Symposium on Circuits and Systems.[S.l.]：IEEE Press，1998：198-201.

[17] Yeo H K，Sharif B S，Hinton O R，et al.Improved RLS algorithm for time-variant underwater acoustic communications[J].Electronics Letters，2000，36：191-192.