不同类型多小波在GPS 变形数据处理中的应用

何永红 靳鹏伟

（1.湖南科技学院 土木工程与建设管理系，湖南 永州 425199；2.中南大学 测绘与国土信息工程系，湖南 长沙 410083）

1 引 言

现实世界中许多灾害的发生与变形有着极为密切的联系，例如地震、滑坡以及桥梁的垮塌等，都是典型的变形破坏现象。随着各种大型建筑的大量涌现以及滑坡等地质灾害的频繁发生，变形监测研究的重要性更加突出，推动着变形监测理论和技术方法的迅速发展。全球定位系统GPS 具有全天候、无需通视、自动化程度高且能够测量建筑物的绝对位移量等优点，特别是近年来，GPS 卫星和接收机性能的大幅度提升[1]、高效的GPS 单历元定位算法的提出，促使基于GPS 的工程建筑物健康监测成为GPS 和土木结构工程领域中的一个研究热点[2,3]。GPS 测量由于受对流层、电离层折射、卫星与接收机钟差、多路径效应等受各种因素的影响，原始数据往往含有较大的系统偏差或者被噪声严重污染，使GPS 信号受到严重的干扰[4]，进而使测量结果难以达到预估及规定的精度要求。如何从观测数据中去掉噪声，保留真实信号，是变形监测与变形分析需要解决的问题。

小波分析技术既能反映信号的时间域变化特征，又能反映信号的频率域变换特征，用它可分析处理各种类型的信号，并已取得了显著的效果[5,6]。在信号处理中，小波基是否具有对称性、正交性、短支撑性、高阶消失矩对处理的结果往往至关重要，但传统的实系数单小波并不存在上述性质，这限制了小波的应用。而多小波却具有这些性质，它既保持了单小波所具有的良好的时域与频域的局部化特性，又克服了单小波的缺陷，将实际应用中十分重要的光滑性、紧支性、对称性、正交性完美的结合在一起[7]。将多小波分析理论作为数学工具对变形监测数据进行分解和重构，可以取得更好的、更符合实际的变形曲线图。

文章通过GPS 历元定位算法确定接收机的坐标时间序列，获得GPS 监测变形的信息，并应用基于不同预处理方法的多小波分析技术从GPS 单历元定位结果中提取了变形信号，建立基于多小波变形分析模型，并与传统的单小波去噪效果进行比较，为变形监测信号处理开辟一条新的途径。

2 多小波理论

2.1 多小波函数

多小波(Multi-wavelet)理论是近几年来在小波理论基础之上发展起来的一种新的小波构造理论。它是指由2 个或2 个以上函数作为尺度分量生成的小波。与传统意义下的单小波相比，多小波兼有对称性、正交性、紧支性、消失矩等特性，因此被广泛应用于各类信号的滤波。多小波基是由单个小波母函数经过伸缩平移生成的，相应地有多个尺度函数；而单小波仅有一个尺度函数。

同时，多小波函数满足

这里，Hk和 Gk都是r ×r 的矩阵，称为双尺度方程的矩阵系数。也称为矩阵滤波器系数[8]。

2.2 多小波预处理方法的选择

现在应用最广泛的是GHM 多小波、CL 多小波和cardbal 系列平衡多小波，这些多小波为二重正交、对称的多小波。多小波与单小波的重要区别是对含噪信号进行预处理，由于多小波变换的预滤波器是矩阵形式的，这就要求输入信号也必须是矢量形式，而实际采集到的信号一般都不是矢量形式，所以必须进行预处理才能进行多小波变换，采用多小波对信号进行消噪时，对原始信号的预处理方法有多种，预处理方案不是随意选取的，它与多小波的性质、多小波基有关。预处理方案的选取直接关系到信号处理的效果，不合适的预处理方案将导致非常糟糕的结果，无法达到预期目的。

根据仿真结果，对于GHM 多小波采用GHM.init 预处理方法，对于CL 多小波采用harr 法，cardbal 系列多小波采用平衡多小波法对多小波预滤波器响应改善较好[9,10]。

2.3 多小波去噪效果评价指标[11]

(1) 均方根误差（RMSE）

原始信号与去噪后的估计信号之间的方差的平方根称为均方误差：，其中 f ( n) 是原始信号，为小波滤波后的估计信号。均方根误差越小，滤波效果越好。

(2) 信噪比（SNR）

信噪比是测量信号中噪声量度的传统方法，常被用来作为评价去噪效果的指标，信噪比越高则滤波效果越好。信噪比单位是分贝，其定义为：

(3) 恢复信号的光滑性

一般而言，恢复信号光滑性好，则滤波方法好。

综合考虑，小波滤波去噪性能评价的准则是：对于同一组数据实验，若某种滤波方法获得的滤波效果均方根误差较小、信噪比相对较高、信噪比增益较大、恢复信号光滑性好，则说明该滤波方法的性能相对较好。

2.4 多小波信号去噪原理

多小波与传统小波的去噪原理是相同的，即在多小波分解系数的基础上，根据噪声的先验知识，设置软阈值处理多小波系数，将与噪声相应的多小波变换系数置零，然后利用多小波的重构算法重构信号。与传统小波去噪相比，多小波可以同时具有对称性、正交性、短支撑性、高阶消失矩。所以基于多小波变换的去噪不仅完整保留传统小波去噪的优点，而且有更为灵活更为实用的特点[12]。

图1. 多小波分解与重构原理图

3 不同多小波在GPS 动态监测数据处理中的应用

3.1 试验

为了验证多小波去噪的有效性，实验采用某GPS 点的实测数据进行分析。实验采用北京遥测技术研究所研制的GNSS单频接收机，采样间隔为1s（采样频率为1HZ），数据在2003 年12 月1 日5：34 开始采集，共观测了500 个历元，共视8颗卫星（PRN31 04 08 20 28 07 27 11），最高的PRN31 作为参考卫星，对其数据采用软件进行基线结算，求得待定点在WGS-84坐标系中不同历元时的坐标系列。坐标采用X，Y 和Z 表示，分析中，坐标均值从坐标序列中扣除。结算后的待定点在不同历元时其三维坐标如下图所示：

图2. GPS 点三维坐标序列变化曲线

从图2 中看出，GPS 位移观测的序列数据含有很多毛刺，受到噪声干扰（如多路径效应、随机噪声），监测点的变化趋势湮没在噪声中。为了从其复杂的变化中提取变形趋势，需采用多小波对其进行处理、分析。由前面的预处理方法中可知，GHM 多小波采用基于低频近似的方法、CL 多小波采用Haar 方法以及采用平衡多小波的方法可以取得较好的去噪效果。现采用不同的多小波对信号进行处理，并与传统的单小波进行比较。

3.2 不同多小波去噪结果验证对比

本节GHM 多小波采用GHM.init 方法、CL 多小波采用Haar 方法以及采用平衡多小波的方法对GPS 点变形信号进行处理，并与传统的单小波去噪效果进行比较。图3 即为GHM 多小波采用GHM.init 方法消噪后的信号。

图3. GHM.init 法滤波后坐标序列

由图3 中看出，采用GHM 多小波消噪后的信号反应了该点的位移趋势，去除了噪声，滤波后GPS 测量微小动态变形为2mm，达到了消噪的目的。

现用DGHM 多小波与DB4 小波作比较，采用DB4 小波的原因是其具有四个稀疏的滤波器、正交性和二阶消失矩，这与DGHM 多小波非常相似。在图4 中，实线为DGHM 多小波去噪曲线，虚线为DB4 小波去噪曲线，由图中看出，DGHM多小波滤波后的信号在光滑性和尖峰及突变部分较单小波要好，其消噪误差较之单小波小。DGHM 多小波更适合于对突变和暂态随机信号的消噪，消噪精确度比DB4 小波要小得多，得到了原信号的变化趋势。

图4. GHM 多小波、db4 小波去噪对比

图5 为CL 多小波与db4 小波消噪后的信号对比图，由图5 可知，CL 多小波表现出较好的去噪性质，去除了信号中的噪声，获取的变形趋势与的db4 小波相差不大。

图5. 采用CL 多小波与db4 小波消噪对比

图6为用cardbal3 平衡小波，在GPS 监测数据中消噪。采用平衡多小波消噪后的信号反应了该点的位移趋势，去除了噪声，达到了消噪的目的，并且避免了预处理，节省了运算时间。但平衡多小波尤其是高阶平衡的多小波难以构造，关于如何构造更高阶的平衡多小波以及对高阶的非平衡多小波进行平衡的问题，还需要进一步研究。

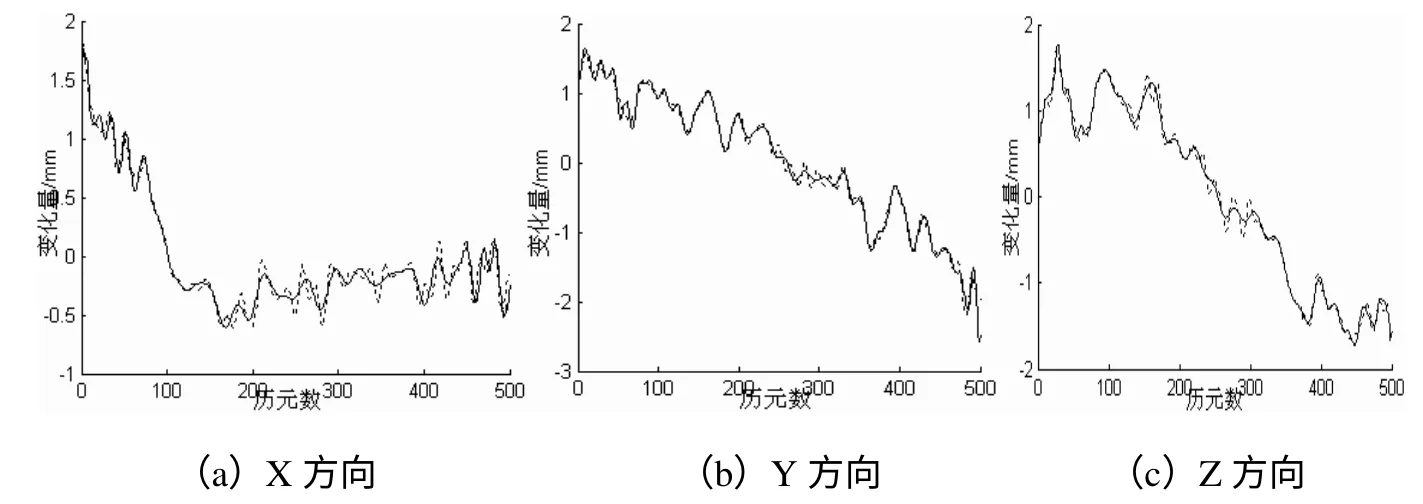
图6. 平衡小波消噪与DB4 小波消噪对比

表1 为GHM 多小波、CL 多小波、Cardbal3 多小波与DB4 小波去噪在信噪比和均方根误差方面的比较， GHM 多小波，Cardbal3 多小波采用合适的预处理方法进行去噪可以达到比单小波还要好的去噪效果，提高了信噪比，降低了均方根误差。CL 多小波去噪效果相对于其他方法较差。

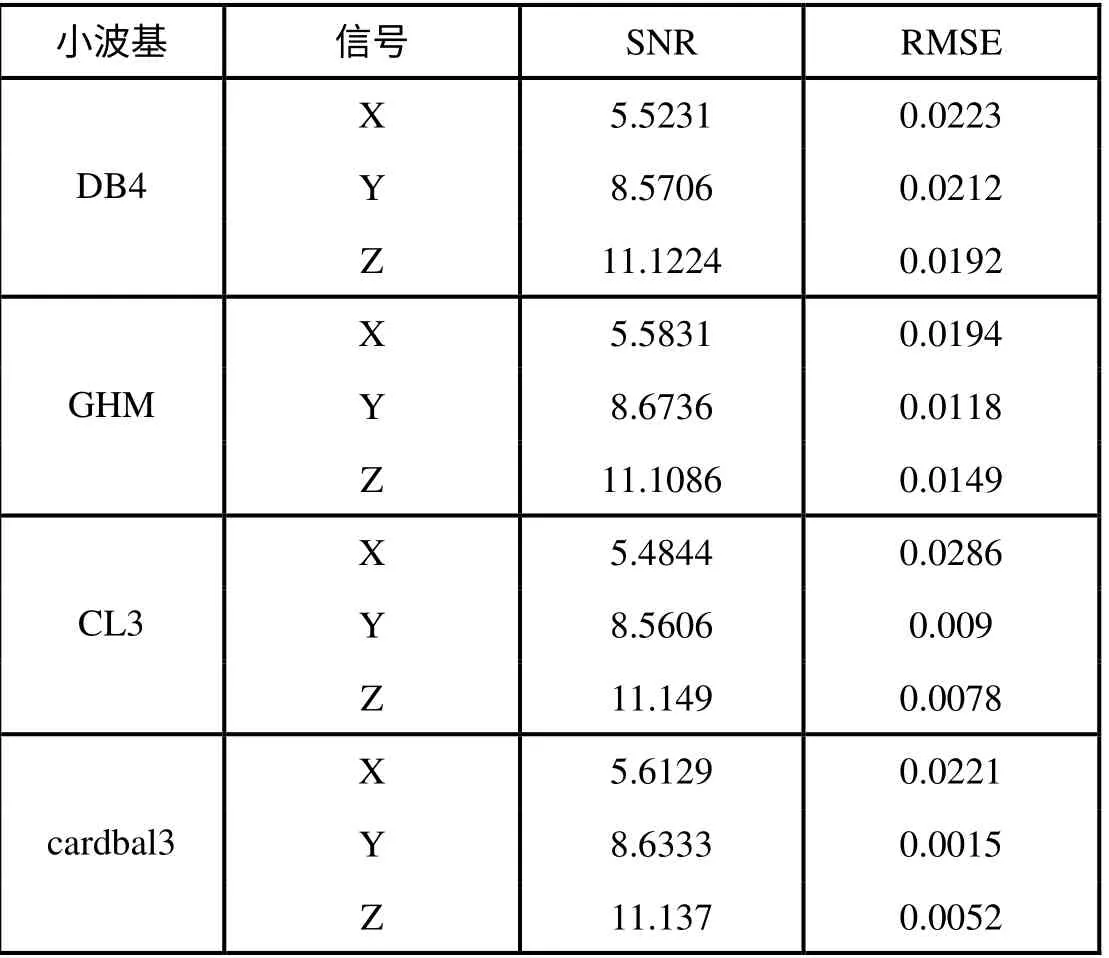
表1. 不同多小波消噪效果比较

4 结 论

多小波是矢量小波，同时具有正交性、光滑性、紧支性、对称性和消失矩等特性，在信号去噪中得到广泛的应用。本文给出基于多小波变换的GPS 信号噪声去除方法，利用预滤波方法对信号进行预处理，多小波对GPS 变形信号进行分析，进而实现噪声的去除，对分析建筑物的变形起到了很好的帮助作用。实验结果表明， GHM 多小波，Cardbal3 多小波采用合适的预处理方法进行去噪可以达到比单小波还要好的去噪效果，CL 多小波去噪效果相对于其他方法较差，是最为适合图像压缩编码的多小波[12]。缺点是利用编程工具实现的多小波去噪程序处理速度比单小波慢，对实验用计算机的性能要求较高。因此，在实际工作应用中，应根据实际信号的特点和工作要求，选用合理的去噪方法，以满足实际的需要。

[1]Ogaja C,Ding X L, Rizos C. Advances in Structural Monitoring with Global Positioning System Technology:1997-2006[J].Journal of Applied Geodesy,2007,1(3):171-179.

[2]Tamura Y,Matsui P L C, Ishibashi R, et al.Measurement of Wind-Induced Response of Buildings Using RTK-GPS[J]. Journal of Wind Engineering and Industrial Aerodynamics,2002,90(12-15):1783-1793.

[3]Kijewski-Correa T,Kochly M.Monitoring the Wind-Induced Response of Tall Buildings: GPS Performance and the Issue of Multipath Effects[J].Journal of Wind Engineering and Industrial Aerodynamics,2007, 95(9-11):1176-1198.

[4]马攀,文鸿雁.离散卡尔曼滤波用于GPS动态变形数据处理[J].桂林工学院学报,2002,22(3):234～238.

[5]吴富梅,杨元喜.基于小波阈值消噪自适应滤波的GPS /INS 组合导航[J].测绘学报,2007,36(2):124-128.

[6]戴吾蛟,丁晓利,朱建军.基于经验模式分解的滤波去噪法及其在 GPS 多路径效应中的应用[J].测绘学报,2006,(4):321-327.

[7]Tai Chiu Hsung,Danielpak-kongLun.Optimizing the multi-wavelet shrink agede-noising[J].IEEE Transactionson Signal Processing,2005,53(1):240-243.

[8]Geronimojs,Hardindp,Massioystpr.Fractal functions and wavelete xpansions based on Several functions[J].Approx Theory,1994,78(3):373-401．

[9]Xiaxg,Geronimojs,Hardindp.Design of Prefilters fordiscrete multi-wavelet transform[J].Trans.OnsignalProcessing,1996,44(1):25-34．

[10]刘志刚,黄慧汇.基于不同预处理方法的多小波暂态信号去噪[J].电子学报,2004,32(6):1054-1056.

[11]王中元,周天强,张鹏飞.高层建筑物GPS 动态变形监测数据处理[J].测绘科学,2012,37(1):47-50.

[12]Chui C K,Lian J.A study of orthonormal multiwavelets.Applied Numerical Mathematics[J].1996,20(2):273-298．

[13]Yong Hong He,Hong Yan Wen,and Peng Wei Jin.The Application of Multi-wavelet in GPS Deformation Signal Processing[J].Applied Mechanics and Materials,2012,226-228:1927-1931.