对一道稳度竞赛训练题解法的商榷

陈新华

（常州市第一中学，江苏 常州 213003）

华东师范大学出版社出版的高中物理竞赛考前训练《赛前集训》一书第13页第9题如下：

一个具有正方形截面的均匀长木块浮在水中，这个木块或以两个相对的侧面平行于水面，或以4个侧面都和水面成45°角，如图1所示，试问其平衡后的位置可能是图中的哪一种？说明理由（设水的密度为ρ0，木块的密度为ρ）.

图1

原书所给的参考解法如下：

图2

点评：这是一个比较物体稳度的计算题，一般来说，稳度跟物体的重心高度和支面大小有关，重心越低、支面越大时稳度越高.本题就是根据重心的高低来判断物体的稳定程度.其关键就在于判断ha和hb的大小.参考解法的（2）、（3）两问中，分别算出了ha，hb，比较两者大小时，用了极限法比较，但极限法讨论的重要前提是函数必须是单调变化的，实际上，由第（2）问的数据，k增大，ha，hb都增大，单从k＝1这一特殊点来比较两者的大小，显然是不够严密，而笔者通过以下运算，发现（2）、（3）两问的条件下并非单调函数，用特殊点的运算来代表整个过程显然是不严密的.

以上是笔者对此题解法严密性的一些补充.仔细分析，不难发现用几何方法解决此题更为便捷.

如图3，按1、2、3三条虚线所示的位置来考虑.

图3

图4

图5

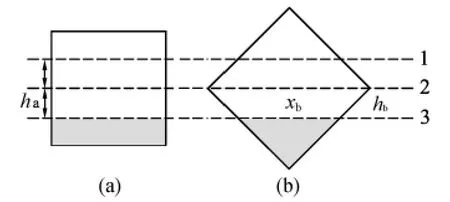
图6

图7

反思：这是一个关于稳度问题的讨论题，但却向我们展示了求极值和比较大小问题的一般处理方法：作差求函数的极值，本题中作差所得的函数比较复杂，带有根号，所以并没有直接求函数的极值，而是用解不等式的方法间接求临界值进行讨论.也提醒我们除非已经很明确函数的单调性，否则用某些特殊点的值来代表整个函数进行比较，往往会失之不严密.

用几何方法讨论，大大减少了运算量，避免了解二次函数，并且物理意义较为明晰.但几何方法解题对物理思维的要求较高，辅以几何图形和辅助线则可以提高处理问题的精确性.