一种新的灰色马尔科夫预测模型及其应用

杜 雯

(鄂东职业技术学院，湖北 黄州438000)

现代奥林匹克运动会是展示世界各国最高竞技运动水平的舞台，其所获奖牌数及国家排名不仅是一个国家体育运动竞技水平的标志，也是国家经济政治和综合实力的体现［1－2］。奥运会奖牌预测问题也是经济学领域研究的热点问题之一，其理论发展一直受到关注，产生了众多预测方法［3－6］，如趋势直线外推法、统计回归方法、色预测模型、时间序列预测法、Markov 方法等。

本文将灰色预测与马尔科夫预测模型相结合，提出了一种新的灰色马尔科夫预测模型，并通过对奥运会奖牌数进行分析预测，结果表明该模型能够降低运算量，提高预测水平，并克服了传统奥运会奖牌数预测模型的不足。

1 灰色马尔科夫预测模型

灰色马尔科夫预测模型的基本思路是:先建立灰色GM (1，1)模型，求出其预测曲线;再以平滑的预测曲线为基准划分若干动态的状态区间，计算出马尔科夫预测未来状态，从而得出预测值区间，取区间中点，最终得到精度较高的预测值。

⑴GM(1，1)模型

①原始数据的累加处理

设原始数据序列为x(0)(1)，x(0)(2)，…，x(0)(n)，记为:

对序列x(0)作一次累加处理，得到新的生成序列为:

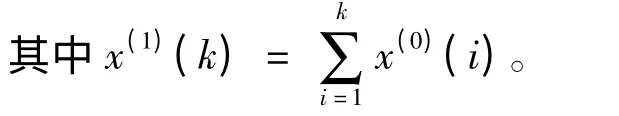
累加生成序列克服了原始数据序列的随机性和波动性，将原始数据序列转化成规律性较强的递增数据序列，其目的是为建立微分方程形式的预测模型作好准备。

②GM(1，1)模型的建立

微分方程(1)就是灰色GM(1，1)预测模型［4－6］，其中a，u为常数，可通过最小二乘法拟合得到:

⑵马尔科夫预测

对于一个符合n阶马尔科夫非平稳随机序列y(k)，其任一状态Qk可表示为Qk∈［Q1k，Q2k］，其中为原始数据的均值。根据所研究对象的实际意义和样本数据的多少来确定Qk的含义，以及状态划分的数目和常数ak，bk的值。由状态Qi经过k步转移到Qj的次数记为nij(k)，状态Qi出现的次数为ni，则由状态Qi经过k步转移到Qj的转移概率为pij(k)=则k步转移矩阵记为P =(pij(k)m×m)，于是系统未来时刻最可能的预测值为

2 灰色马尔科夫预测模型在伦敦奥运会奖牌数预测中的应用

根据第24 届至第29 届奥运会奖牌榜情况，选取多次出现在奖牌榜前10 名的5 个国家［7］，并重点参考近两届的排名情况，其基本情况如表1 所示(其中俄罗斯数据的第25 届为独联体的数据，第24 届为前苏联的数据，德国第24 届的数据为民主德国和联邦德国的奖牌数和)。

对于表1 中的相关数据，依次对中国、美国、俄罗斯等国家编号i=1，2，…，5，将剩余的国家和地区的综合编号i=10，由此确定了所要研究的10 个国家或地区。

在计算奖牌数比例时必须考虑到“东道主效应”［8］。竞技体育中的“东道主效应”是指运动员在自己的家乡参加比赛要比在其他地方参加比赛能取得更好的成绩。邓运龙统计了1992 －2000 年这3 届奥运会中，东道主举办当届、上一届、再上一届和后一届获得金牌、奖牌排名情况，论证了夏季奥运会确实存在着东道主效应［9］。对于“东道主效应”的测算有很多方式，选用参考文献［1］中简单平均法综合所有各届奥运会东道主效应，所得结果是:金牌数的东道主效应增幅为11.31%，整体实力的东道主效应增幅为11.71%。而第30 届奥运会时中国队是客场作战，因此需要在每届奥运会中去除东道主效应对奖牌数的影响。选取东道主效应指数α=0.1171，则去除东道主效应后东道主奖牌数

表1 第24 届至第29 届奥运会奖牌榜

在所研究的数据中有东道主效应的国家有第26 届的美国，第27 届的澳大利亚，第29 届的中国，奖牌数分别为101，58，100 枚，按折合后奖牌数分别为91，52，90 枚，将其折合后统计每届中各国奖牌数见表2 所示。

表2 去除东道主效应后的奖牌数统计表

根据表2 中各国家或地区奖牌数ni(t)与总奖牌数N(t)，由式计算得到各国家或地区奖牌数比例如表3。

表3 各国家或地区奖牌数占总奖牌数的比例

下面运用上文提出的灰色马尔科夫预测模型对第30 届伦敦奥运会中国获奖牌所占比例进行预测。

Step1:构造奖牌比例序列

对x(0)进行一次累加生成，得生成序列

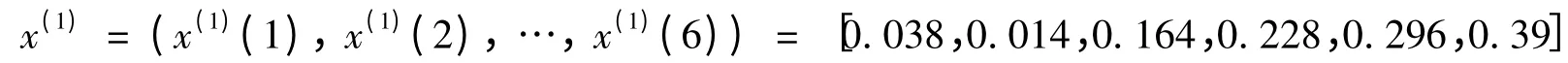
Step2:构造数据矩阵B及数据向量Y

Step3:计算^a

于是得到

Step4:建立模型，得预测方程

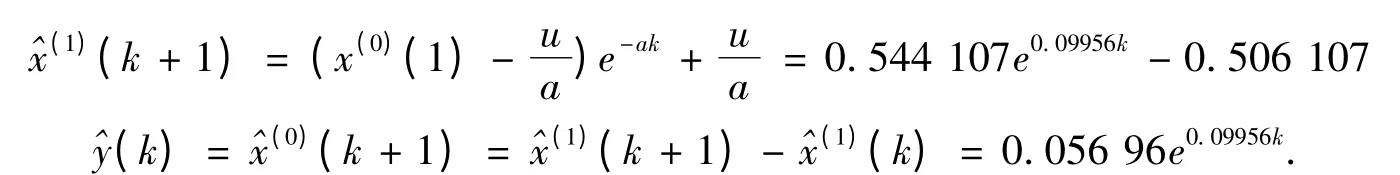
Step5:以(k)曲线为基准，划分成与(k)曲线平行的三个区域，每一个区域构成了一个状态如下图1 所示。

图1 预测方程状态图

其中(k)为第k年的预测值，为历年奖牌比率的平均值0.065。由图1 可知，落入Q1，Q2，Q3三个状态的原始数据的样本点数分别为n1=n2=n3=2。由状态Q1一步转移到状态Q1、Q2和Q3的原始数据样本点数分别为n11=1，n12=1，n13=0;由状态Q2一步转移到状态Q1、Q2和Q3的原始数据样本点数分别为n21=0，n22=1，n23=1;由状态Q3一步转移到状态Q1、Q2和Q3的原始样本点数分别为n11=0，n12=1，n13=1。故可得一步转移概率矩阵为

根据该矩阵可以判定2012 年中国所获奖牌率最有可能处于状态Q3，即可能在灰区间［Q31，Q32］内，因此2012 年的中国所获奖牌率预测值

同样用此方法可依次计算出各个国家或地区奖牌比率。再根据各届的奖牌总数假设下届的奖牌总数为960 枚，最后求得第30 届奥运会各国家或地区奖牌比例和数量情况如表4 所示。

表4 第30 届伦敦奥运会各国家或地区奖牌比例和数量预测值和实际值比较

由表4 可以看出，整体的预测效果比较好，预测的平均相对误差均在7%以内。因此，可运用该预测模型来预测第31 届里约热内卢奥运会世界各国的奖牌数，预测值的可信度将比较高。

本文将灰色理论与马尔科夫预测相结合，提出了灰色马尔科夫预测模型。灰色GM (1，1)预测所需信息较少，计算简便，但由于GM (1，1)模型的解为指数型曲线，其预测的几何图形是一条较平滑曲线，因而对波动性较大的数据列拟合较差，预测精度较低。而马尔科夫模型适合于波动性较大的数据列预测问题，但它要求研究对象具有平稳过程等特点。因此，本文将两者取长补短结合起来，形成了灰色马尔科夫预测模型，该模型可有效提高随机波动较大数据列的预测精度。

［1］ 王国凡，唐学峰. 奥运会奖牌预测国内、外研究动态及发展趋势［J］. 中国体育科技，2009，45(6):130 －132.

［2］ 王宇鹏，许健. 奥运会奖牌榜影响因素的实证分析［J］. 统计研究，2008，25(10):57 －62.

［3］ 张正民. 奥运会男子100m 跑成绩的灰色GM(1，1)模型预测［J］. 体育学刊，2011，18(4):112 －114.

［4］ 肖新平，宋中民，李峰. 灰技术基础及应用［M］. 北京:科学出版社，2005.

［5］ 邓聚龙. 灰预测与灰决策［M］. 武汉:华中科技大学出版社，2002，60 －65.

［6］ Rao C J，Peng J，Li C F，Li W. Group decision making model based on grey relational analysis［J］. The Journal of Grey System，2009，21(1):15 －24.

［7］ 张玉超. 第29 届奥运会中、美、俄国奖牌分布特点及其启示［J］. 体育学刊，2009，16(2):81 －84.

［8］ 吴殿延，吴颖. 2008 北京奥运会中国金牌赶超美国的可能性［J］. 统计研究，2008，25(3):61 －64.

［9］ 张海波，赵焕成. 北京奥运会中国军团金牌数的预测［J］. 统计与决策，2008，15:76 －77.