图形推演中线状目标的爬行效果研究

聂 颖，窦长旭

（中国电子科技集团公司第十五研究所 地理信息与图形图像技术研发中心，北京 100083）

随着计算机信息化手段的日益普及和发展，以矢量图形动画实现为核心的图形推演技术已被广泛地应用于仿真模拟、情况汇报和态势推演等各类军事应用中，以达到帮助使用者更好地展示仿真过程、汇报值班情况或推演作战谋划的目的[1]。

图形推演主要负责完成目标和场景的动态表达定义和演播，是图形处理平台的一个组成部分，其依托于图形数据管理和图形符号库，为最终上层应用提供图形动画支撑，是态势推演应用的关键部分。目前，许多动画推演和图形处理类的软件[2-3]都具备了图形推演的基本能力，基本都实现了目标基本动作的设计，但对动作动画效果的精细性和准确性缺少深入的研究，往往止步于示意阶段。本文将介绍图形推演在线目标移动效果方面的研究成果。

1 系统概述

图形推演的系统结构如图1所示，分为核心处理和应用两个层次，核心处理层负责数据的生成、显示、驱动和控制，应用层负责提供操纵目标数据和动态数据的各类界面操作。

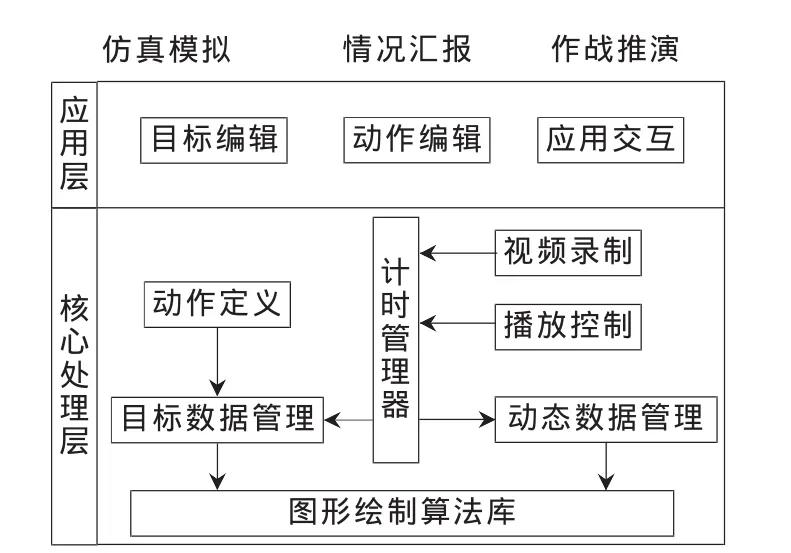
图1 图形推演的系统结构

图形推演系统的外围是以图形推演作为支撑平台的推演类应用。

目标数据管理模块负责目标静态数据的管理，处理数据的生成、修改和删除。目标数据通过调用图形绘制算法库提供的相应算法完成显示绘制。

动作定义模块为目标对象添加动作，追加到目标数据的动作属性中。根据实际的需要，还可以设计动作组和动作集合，实现复合动作的定义和播放。

计时管理器是推演技术的重要部分，负责按计时器的单位时间间隔从目标数据管理模块获取相关数据，生成当前时刻的动态数据，并记录在动态数据管理模块。

动态数据是变化了的静态数据，其初始显示姿态和目标静态数据本身相同，但随着时刻的变化，目标的显示效果也会变化。动态数据的显示也要依靠图形绘制算法库完成。依据动作类型的不同，数据变化的方式也不相同。

播放控制主要负责对计时管理器的控制，通过启动、播放、暂停、停止和定位等指令，控制推演的工作时刻。

视频录制提供了与外部应用的标准接口，实现推演制作的数据共享。录制的过程也要靠计时管理器一帧一帧地推送渲染。

2 爬行动作定义

图形数据动态表达的基本单位是动作，描述一个动作的基本参数包括动作标识、动作名称、起始时间和结束时间，而根据动作类型的不同，动作参数也各不相同。图形推演支持的常用基本动作包括显示/隐藏、闪烁、旋转、按轨迹移动、生长和变形等。

在战场态势推演过程中，随着时间的推移，一些实体的空间位置会发生改变（如战役中部队的行进，飞机对敌方进行空袭等），这就需要定义一个按轨迹移动的动作，其动作参数为起始时间和移动路线轨迹，前者是线目标移动，后者是点目标移动。点状目标移动相对简单，可以通过设置标号的位置和方向角来体现，但对于线状目标按轨迹的移动，理想效果是使线目标在路线上贴合爬行，因此又称之为爬行动作定义。

3 爬行效果研究

3.1 问题描述

效果指各类推演动作在播放时呈现出的结果，主要由动态数据管理和图形绘制算法库两个模块来完成。

对于爬行效果来说，目前大多数研究者[4]采用的方法都是解决线标首尾两点的轨迹拟合，中间的点通过设置间隔容限和差值来实现。这种算法虽然通用，但没有考虑线标实际含义和线标本身的拟合算法，导致在展示效果和准确性上都存在局限性，在实际推演播放中会呈现比较突兀的显示姿态，导致轨迹发生跳跃、偏移。

以带有宽度的箭标为例，假设其在一条有变化的道路上爬行，如图 2（a）所示。箭标有 3个定位点，Ps为起始点，Pe为结束点，Pn为中间点，图2给出了3个时刻的箭头移动结果，第 1时刻 3点序列为{Ps，Pn，Pe}，第 2时刻 3 点 序 列 为{P′s，P′n，P′e}，第 3 时 刻 3 点 序 列 为{P″s，P″n，P″e}。

可以看出，如果只采用箭标首尾两点与轨迹拟合的简单办法，则中间点Pn轨迹是否可重合是随机的。如果轨迹的坡度平缓，则拟合度好一些；如果轨迹变陡峭，则显示姿态就比较生硬。

另一方面，对于走向变化特别大的路径，即使每个爬行点都在路径上，依然不能很好地拟合，如图2（c）所示。因为以当前的点数，不可能拟合出变化这样大的箭头曲线。因此，要做到每一时刻的箭标都较好地与路径拟合，不仅需要把每个点都修正到路径线上，点数的密度也必须适合，如图 2（d）所示。 在图 2（b）中，不仅 Pn点3个时刻都落在路径上，并且点数上也有所增加，第2时刻和第3时刻都增加了点数Pn-1。

图2 问题效果和期望效果对比图

但是，拟合点的密度也不能简单地理解为越多越好，只要记录表示路径拐点的关键点即可，如图2（d）的情况，只需要6个点。

3.2 改进策略

要达到图 2（b）和图 2（d）的期望效果，需从图形绘制生成和轨迹点生成两个方面细致研究相关算法。轨迹点生成负责按照计时管理器的时间推进，计算出合适长度和密度的轨迹点阵列；再将生成的轨迹点阵列作为箭标的中轴线点阵列输入，通过箭标实现算法拟合出对称美观的箭标符号。

3.3 算法说明

3.3.1 轨迹爬行算法

采用基于特征点的爬行算法计算出正确的位置点和适合的点数。计算步骤如下。

（1）提取整个轨迹的折线逼近点序列 P{0，1，…，n}，这个点序列的密度取上限，足以达到折线拟合曲线的程度。在整个演播过程中，箭标的起点Ps将从轨迹第0点一直移动到第n点。

（2）根据当前时刻ti占总时刻的百分比和箭标的长度计算出ti时刻箭头起点所在的位置 P′s。显然 P′s是轨迹点阵列P中的一点，其下标的计算方法为：

其中，t为总的移动时间，Ii为第 i个拟合点在P点组中的下标，Ipi为ti时刻拟合点 Pi在离散点组中的下标。根据各个拟合点在ti时刻的下标，可获得当前时刻Pi点坐标，P′s=Pi。

（3）依据箭标的概略长度，在P点阵列中，反向计算出 ti时刻时箭尾点的位置 P′e，则 P集合的子集 Pn{P′s…P′e}就是这一时刻的箭标中轴点阵列，Pn∈P。

（4）但是如步骤（1）所述，这个来自轨迹拟合点的 Pn阵列的点非常密集，两点之间的距离一般不会超过2个像素，用这些点来形成贝塞尔曲线的拐点，对于箭标来说，无论从性能还是效果上讲，都有裁剪的必要。

（5）图形推演数据相当于一种时间序列数据，对轨迹数据的裁剪也可以理解为一种数据的聚类运算。对时间序列数据进行聚类的算法有基于距离、基于特征和基于模型等多种算法[5]。这里采用基于特征值的方法进行裁剪，以邻近点之间的坡度和距离作为特征值，对Pn的各个点进行筛除。首先设置计算关键特征点的距离阈值，默认为所有线段长度数学期望的1/2，然后将Pn阵列中的每一点填写特征值矩阵结构，记录每一点和相邻点的距离和角度关系；取每一点和它的相邻两点做三角形，计算该点的尖角和对应边长度与折线总长度的比例值，小于角度阈值和比例阈值的点即被筛除。

（6）特征点计算完成后，形成 Pj阵列，Pj∈Pn∈P。

（7）将形成的 Pj点阵列送至图形绘制算法库，绘制当前时刻的箭标。

（8）这一时刻的推演步骤完成，计时管理器启动下一时刻的数据推送与绘制，重复上述步骤。

3.3.2 箭标绘制算法

箭标大致分为箭头和箭身两部分。箭头又可分为箭颈、箭耳和箭尖3部分，箭身则由左、右箭身和箭尾组成。一般来说，箭身两侧为贝塞尔曲线，以保证箭身的美观平滑；箭头采用直线绘制，以保证箭耳和箭尖的锐利效果。

要实现箭标在路径上的严格爬行，箭标本身的绘制算法也很重要，需保证给定了合适的箭头中轴线的情况下，箭标的两侧曲线仍有良好的平行度，如图3所示，P0~P5即为箭标的中轴线。

图3 箭标组成图

图3中，箭头由 7个点组成，其中第 4点位置已经确定，即箭标中轴线的最后一点。根据箭头角度、箭耳角度和箭头占箭标总长的比例，就可以计算出其他6个点，这里不再赘述，重点介绍箭身的生成算法。箭身的生成算法如下。

（1）去除中轴线点阵列中的箭尖顶点，计算第 1点到第n-1点的总长度L。

（2）计算箭身贝塞尔曲线的拐点位置到中轴的距离Gdw序列，第i点的拐点宽度计算公式为：

其中，Neckw为箭颈宽度的 1/2，Tailw为箭尾宽度，L为箭标中轴线的总长度，△ln为当前点与前一点的距离，rss为箭头收缩系数。

计算时采用了指数型的非线性收缩算法，这是式（2）的一个关键点。由于最终目的是为了算出表示箭身曲线的拐点位置，如果各个拐点间的位置都是线性关系，拟合出的贝塞尔曲线不但收敛速度慢，且线条走向也会比较僵硬，不够自然光滑。因此，这里采用指数系数来改变拐点阵列的走向、平滑度和收敛速度。

（3）根据拐点宽度Gdwi生成中轴线点两侧的拐点坐标左点阵列 L{1，…，n-1}和右点阵列 R{1，…，n-1}，计算方法如图4所示。已知 Si-1、Si、Si+1为箭标中轴线上的3点，3点组成一个三角形，计算过Si点与Si-1和Si+1连线平行的线段，线段两个端点分别为P和Q；再采用定比等分算法，即计算出Li和Ri。公式如下：

图4 拟合曲线生成算法图

（4）获得了 L和 R点序列，取默认调整比例，就可以拟合出过这些拐点的贝塞尔曲线；按照左箭身—箭头—右箭身的顺序，将集合点序列送入直线绘制函数，即完成了当前时刻箭标的效果显示。

4 实验结果

图5为“燕尾行动箭标”进行爬行移动的效果截图。经实验表明，爬行效果在各个弯度上都基本保持了尺寸不变和精确拟合。图 5（a）为第3 s刚刚开始起步的效果，图5（b）为第11 s行动箭标在弯路上爬行的效果。

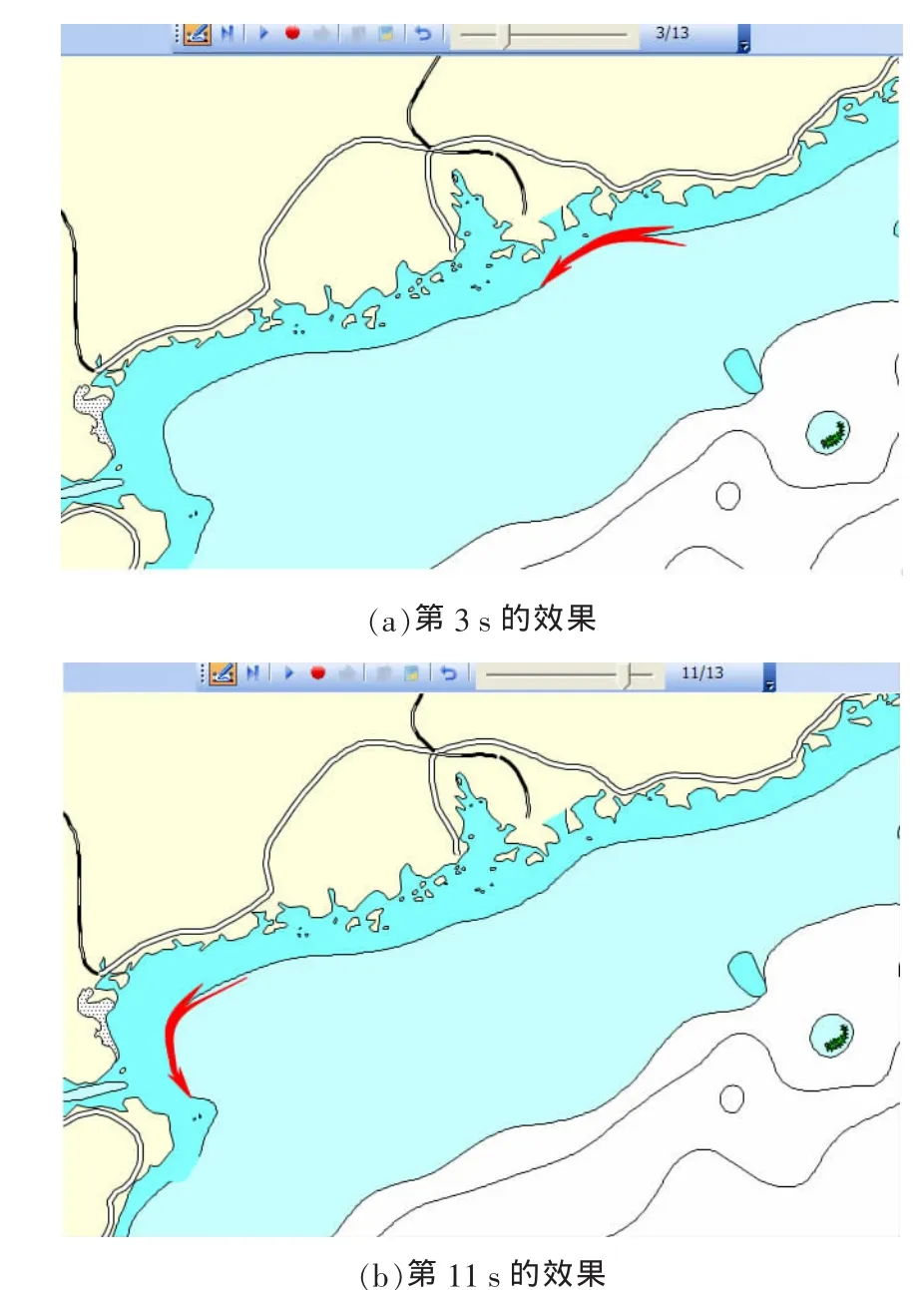
图5 线目标爬行效果截图

本文提出的线标爬行算法有效解决了线标移动的轨迹偏移问题，改善了以往按轨迹移动的动画实现大多只重视点状目标的实现，线状目标的移动只关注首尾点或中心点的缺陷。

图形推演技术被用于多种军事应用场景中，但不同应用场景（如作战推演[7]、交接班汇报和想定仿真）在应用流程上还有很多差别，如前两者的数据大多来自人工生成，而后者则主要是数据自动生成。如何整合这些应用场合的相同点和不同点，保证不同工作方式下动作参数获取的一致性，是今后研究的一个主要方向。同时，研究多个目标同时动作下的时间同步和提速策略，也是影响效果进一步优化改进的重要因素。

[1]陈康，徐培德，马满好，等.态势推演系统结构研究[J].军事运筹与系统工程，2005，19（3）：43-47.

[2]张宝印.基于矢量的时序图形图像处理技术的研究与实践[D].郑州：中国人民解放军信息工程大学，2001.

[3]何忠焕，边馥苓.GIS系统下二维地图推演技术的研究[J].武汉大学学报（信息科学版），2005，30（1）：69-72.

[4]张欣，张立立，曹国峰，等.战场态势推演 GIS动态表达技术与应用[J].地球信息科学，2006，8（4）：80-83.

[5]赵恩来，郝文宁，赵水宁，等.改进的基于密度方法的态势聚类显示算法[J].计算机工程，2010，36（18）：35-37.

[6]杨瑞平，张小京，赵东波.推演系统中面向角色的二维态势研究 [J].系统工程与电子 技术，2007，29（12）：2093-2096.