基于中位数回归模型非寿险精算中费率因子的显著性判别分析

郭念国

（河南工业大学 理学院，郑州 450001）

0 引言

在非寿险精算领域，如何厘定出价格合理、具有竞争性的保险产品是保险人关注的一个重要问题。因为产品的价格不仅仅关系到新客户的加入，还影响到老客户的去留，而且价格合理的保险产品在一定程度上可以避免被保险人出现道德风险和逆选择，从而减少保险人不必要的损失。分类费率厘定方法作为非寿险精算中费率厘定最重要的方法之一，其基本思想是基于保险市场中被保险人的风险水平的不同进行分组划分，对不同的风险组别分别厘定费率，而辨别各个风险组别之间是否存在显著性差别，是厘定费率的一个前提条件。广义线性模型作为分类费率厘定的一个重要统计工具，在非寿险精算领域取得了大量的研究成果。

分位数回归作为线性模型的推广，可以通过选取不同的回归分位，更全面的刻画条件分布，而且其具有参数估计的稳健性和单调变换不变性等优良特性。实践证明Koenker[1]，在满足广义线性模型假设的条件下，利用分位数回归模型估计的结果与广义线性模型的估计几乎一致；如果假设条件不满足，分位数回归估计的结果会更好，从而，使得分位数回归的理论和方法在各个领域的研究应用得到迅速发展。郭念国和徐昕[2]利用分位数回归模型对非寿险精算中厘定变量对损失变量的影响进行了整体分析，但利用分位数回归模型研究非寿险精算中问题的文献尚不多见。

本文基于中位数回归模型的优良性，对费率因子水平的显著性进行判别，并与其他模型进行比较。为更好的理解中位数回归模型，本文首先介绍了中位数和中位数回归模型的概念及其实现算法；然后基于中位数回归模型的思想和算法，对中位数回归估计的优良性进行了说明；最后给出实证分析。

1 中位数及中位数回归模型

中位数是分位数的一个特例，样本中位数一般定义为有序集合的中间值，即样本中位数把样本分成数目相等的两部分，一部分均大于中位数，另一部分均小于中位数。通常用样本中位数来估计总体中位数m，即如果变量Y代表总体，则

定义1 设随机变量Y的累积分布函数为F(y)=P(Y≤y)，则Y的中位数为QY(0.5)=min{P(Y≤η)≥0.5}。

由中位数的定义可以看出，中位数只与其所在序列的位置有关，从而比均值更具有稳定性。如调查某社区的家庭收入情况，因为客观原因，可能只有少数的家庭收入很高，从而该分布是右偏的，用中位数代表家庭收入比均值更能反映多数家庭收入状况。

定义2 设(yi,xi)为第i个观测值，其中xi=(xi1,xi2,…,xip)T，i=1,2,…,n，称下式为中位数回归模型。

其中β0.5为下式的解

2 中位数回归的优良性

2.1 稳健性

稳健性考虑的问题是：当实际模型中的分布与假定模型中的分布有微小差异时，统计方法的性能会受到怎么样的影响。基于Hampel[5]提出的影响函数，下面给出中位数回归模型具有稳健性，而均值模型不具有。

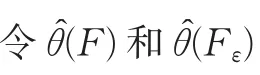
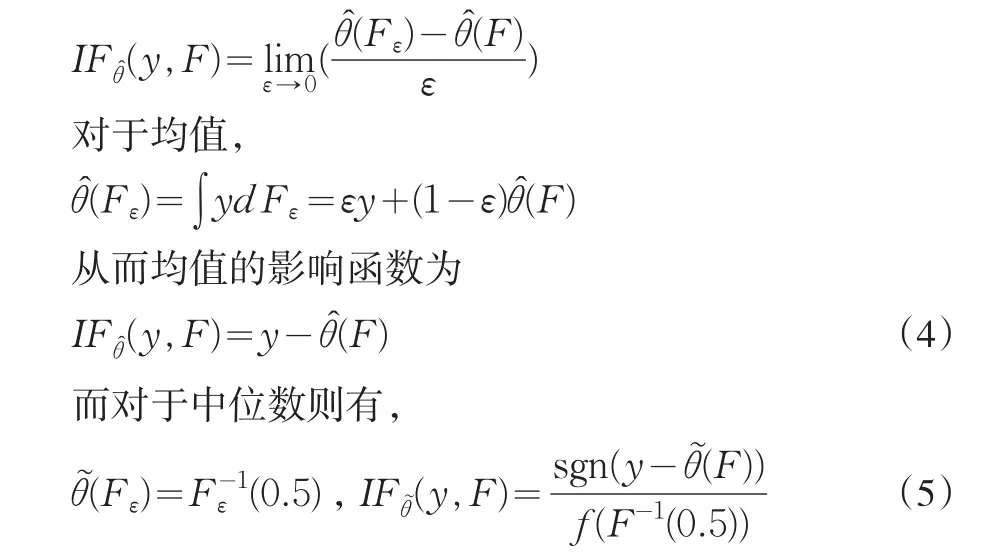
假定式（5）中分母存在且大于零。

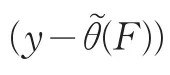
2.2 单调变换的不变性

一个好的统计模型，不仅仅具有稳健性，而且还应该具有变量变换的不变性。如一个索赔额y（以美元为单位）的统计模型，若变换索赔额y的度量货币，如人民币，希望这种变化对模型的估计结果没有影响；如果对模型中的因变量作变换，也希望模型中的参数发生同步变化，而模型解释的结论并不改变，这就是模型的单调变换的不变性，中位数回归模型就具有该性质。

假如h(⋅)是实数R上的非减函数，对于任意的随机变量Y，下式成立

称（6）式为分位数的单调变换不变性。

式（6）成立是因为

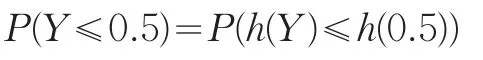
由式（6）可知，对变量Y做h(⋅)变换后的中位数等于Y 的中分位数做 h(⋅)变换。由式（6）和式（1）知，

其中X为协变量。从而，中位数回归模型对于变量Y做变换h(⋅)后的中分位数的值大小没有发生变化，即模型的结论没有变化，称该性质为中位数回归模型的单调变换的不变性。该性质对于线性模型不成立，因为E(h(Y))≠h(E(y))，除非 h(⋅)是妨射变换。

3 实证分析

本文利用P.de Jong等[6]中分析的车辆保险数据对费率因子的显著性进行分析，该数据是基于2004年或2005年的一年期保单数据，包含10个变量，67856份保单，其中有4624份至少发生一次索赔。设索赔额变量为y（美元），对4624份保单索赔额统计如表1。

由表1可知，索赔额变量y的变异程度非常大，而且中位数与均值的差别很大，说明数据存在厚尾现象。对于存在该现象的数据，Gamma回归模型和逆Gaussian回归模型是两个常用方法。故基于分位数回归模型的费率因子显著性的判别结果将与这两个模型作比较，为此，分位数回归模型需对对索赔额变量y进行对数变换，由性质（7）知，该变换对分位数回归模型的估计结果没有影响。

为与P.de Jong等[6]中的结论比较，本文讨论驾龄类别（agecat）、性别（gender）和区域（area）三个费率因子对索赔额的影响，它们分别有6、2和6个水平，取值及基准水平的选择如表2。

为分析析各个费率因子水平对索赔额的显著性，建立的均值回归模型和分位数回归模型分别为

表1 索赔额的描述性统计

表2 费率因子

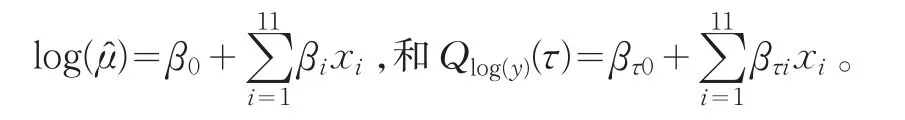
表3给出Gamma回归模型、逆Gaussian回归模型和中位数回归模型中费率因子水平参数的估计值及其显著性，其中分位数回归模型的估计是基于Koenker[7]中rq函数，其他两个模型是基于R Development Core Team[8]中的glm函数，模型中参数的估计方法均为函数中默认的方法。

由表3知截距项，即行驶区域在C、驾龄类别为3的男性保单持有人对索赔额有显著（本文的显著性均基于0.05的显著性水平）影响。数据删除前后，三个模型给出了相同的结论。当然，对索赔额影响的大小，在数据删除前后，Gamma回归模型与逆Gaussian回归模型给出的估计值比中位数回归模型均大，这与表1中索赔额的描述统计相符合，同时也表明数据中存在右偏、后尾现象。但数据删除前后截距项估计值变化，中位数回归模型仅有0.087，而Gamma回归模型与逆Gaussian回归模型均超过0.4，是中位数回归模型估计变化的近四倍，这说明中位数回归模型对数据更具有稳健性。

表3 不同统计模型费率因子估计结果

对于驾龄类别费率因子各个水平的显著性，在数据删除前，三个模型给出了完全相同的结果，即认为驾龄类别1的保单持有人发生的索赔额与基准水平驾龄类别3发生的索赔额有显著差异，其他驾龄类别的保单持有人与基准水平发生的索赔额没有显著差异。在数据删除后，Gamma回归模型与逆Gaussian回归模型给出的结论与没有删除数据的结论相同，即驾龄类别1的保单持有人发生索赔额比基准水平显著的高，从而应收取更高的保费。

对于性别费率因子，在数据删除前后，Gamma回归模型与逆Gaussian回归模型给出相反的结论。数据删除前，这两个模型均认为，女性保单持有人与基准水平的男性保单持有人发生索赔的额度有显著差别，并认为女性保单持有人发生的索赔额小；但是在数据删除后，则认为男性和女性保单持有人发生的索赔额没有显著差别，即认为性别对索赔额的影响没有差异，这说明模型不具有稳健性。而中位数回归模型在数据删除前后均认为，性别对索赔额的影响无差异，应当收取相同的保费。

对于区域费率因子各个水平的显著性，对于行驶区域在A、B、D和E的保单持有人，数据删除前后，三个模型均认为与基准水平行驶区域C的保单持有人发生的索赔额没有显著差异。但对于行驶区域在F的保单持有人，在显著性水平0.05下，数据删除前后，Gamma回归模型与逆Gaussian回归模型给出了不同的结论。数据删除前，这两个模型认为行驶在该区域的保单持有人与基准水平有显著差异，而且发生的索赔额较高，相对于基准水平风险较大，从而应收取较高的保费。但在数据删除后，则认为区域F与行驶在其他区域的保单持有人一样，风险大小并没有显著性差异。而中位数回归模型在数据删除前后，给出相同的结论，即认为行驶在各个区域的保单持有人风险大小没有显著差异。这进一步表明，中位数回归模型的稳健性。

为进一步说明中位数回归模型的优良性，可以对Gamma回归模型与逆Gaussian回归模型中参数进行Wald检验Draper和Smith[9]，进一步比较费率因子各水平之间是否具有显著性差异。假设行驶在区域F和区域E的保单持有人具有相同风险，对此作Wald检验，在数据删除前，Gamma回归模型的χ2检验统计量值为7.2，p=P(χ2＞7.2)=0.027 ，在0.05显著性水平下，拒绝原假设，即认为行驶证区域F的保单持有人确实与行驶在其他区域的保单持有人具有不同的风险水平；逆Gaussian回归模型对该假设给出的 χ2检验统计量值为4.9，p=P(χ2＞4.9)=0.086，从而认为行驶证区域F的保单持有人与行驶在其他区域的保单持有人具有相同的风险，从而两个模型在数据删除前就给出了不同的结论。对于数据删除后，Gamma回归模型的χ2检验统计量值为2.9，p=P(χ2＞2.9)=0.24，从而给出相反的结论，即认为行驶在区域F和E的保单持有人具有相同的风险；逆Gaussian回归模型对该假设给出的 χ2检验统计量值为2.6，p=P(χ2＞2.6)=0.27，数据删除前后给出了相同的结论。对于其他的费率因子同样可以进行Wald检验，进一步比较费率因子各水平之间是否具有显著差异。

综上所述，仅仅利用Gamma回归模型与逆Gaussian回归模型参数的显著性水平往往会给出错误的判断，尤其是数据中存在巨额索赔额时，往往会影响费率因子水平的显著性，而且数据删除与否会给出不同的结论，结合Wald检验在一定程度上弥补了这两个模型的不足。但是中位数回归模型则给出了更为准确的费率因子水平的显著性与否的信息，从而可以为分类费率厘定方法提供更好的费率因子信息。

当然，中位数回归模型不是绝对完美，对于驾龄费率因子水平1，数据删除前后，中位数回归也给出了相反的结论。产生这种现象的原因在于删除数据时，驾龄费率因子水平1相对其他水平删除的观察数据较多所导致的。即使不去深究发生该现象的原因，相对于Gamma回归模型与逆Gaussian回归模型来说，中位数回归模型的误判，至少对于该组数据来说其误判更低。

4 结语

分类费率厘定方法作为非寿险精算中费率厘定最重要的方法之一，通常都是基于损失分布假设的条件下，通过检验模型中参数的显著性与否进行判定，而损失分布模型的选择往往具有一定的主观性。中位数回归模型不仅具有稳健性，而且具有单调变换的不变性，结合实际数据进行拟合分析表明，中位数回归模型比常用的Gamma回归模型和逆Gaussian回归模型在费率因子的显著性方面更具有优良性。费率厘定问题作为非寿险精算中的一个重要研究内容，中位数回归模型可以作为广义线性模型的一个有益补充。

[1]Koenker,R.Quantile Regression[M].Cambridge：Cambridge University Press,2005.

[2]郭念国,徐昕.分位数回归在非寿险产品费率厘定中的应用[J].统计与决策，2010,(24).

[3]Koenker,R.,Bassett G.Regression Quantiles[J].Econometrica,1978,(46).

[4]Hao,L.,Naiman D.Q.Quantile Regressioin[M].Los Angeles：SAGE Publication,2007.

[5]Hampel,F.R.The Influence Curve and its Role in Robust Estimation[J].Journal of the American Statistical Association,1998,(69).

[6]Jong P.D.,Heller G.Z.Generalized Linear Models for Insurance Data[M].Cambridge：Cambridge University Press,2008.

[7]Koenker R.Quantreg：Quantile Regression.R package Version 4.54,[EB/OL].URL http：//CRAN.R-project.org/package=quantreg,2011.

[8]RDevelopmentCoreTeam.R：alanguageandEnvironmentforStatistical Computing.R Foundation for Statistical Computing,Vienna,Austria.ISBN3-900051-07-0[EB/OL].URLhttp：//www.R-project.org/,2010.

[9]Draper,N.R.,Smith,H.Applied Regression Analysis[M].New York：John Wiley&Sons,Inc.,1998.