基于截集的加权可能性均值-方差模型的应用

付云鹏,马树才,宋 琪

（辽宁大学a.信息学院;b.经济学院，沈阳110036）

0 引言

证券市场是一个极为复杂的系统，除了收益和风险本身的不确定性外，由于研究对象的复杂性，对该系统的描述也往往是不确定。这些不确定性因素通常表现为两种形式：一种是事件发生与否不确定性，即所谓的随机性；另一种是事件所处的系统状态自身的复杂性及投资者的主观性导致的不确定性，即所谓的模糊性。这些模糊因素包括政策、经济环境、投资者的主观意愿等这些都是客观存在的。为了全面的考查这样一个复杂的系统，有必要将模糊性因素也考虑到组合投资模型的构建之中。为此许多学者将模糊信息考虑的组合投资模型的构建中，建立了基于模糊因素的组合投资模型。本文将在前人研究成果的基础上以随机变量为模糊数时的加权可能性均值、加权可能性方差和加权可能性协方差为研究对象，将他们分别作为证券未来收益、风险和各种证券的收益率之间相关程度的度量。研究基于截集的加权可能性均值-方差组合投资决策模型的构建方法及模型的实际应用。建模过程中考虑不同投资者的对风险的不同态度，将投资者投资未来收益和风险的乐观程度用乐观系数λ来反映。并将基于截集的加权可能性均值-方差模型与Markowitz均值-方差模型进行对比分析。

1 加权可能性均值和方差的定义及性质

1.1 加权可能性均值的定义及性质

1.2 加权可能性方差与协方差的定义及性质

1.3 三角模糊变量的加权可能性均值、方差和协方差

2 基于截集的加权可能性均值-方差模型的构建

3 模型的应用

表示，其中T为样本数据的时期数。

根据样本数据求得上述八种股票的模糊收益率的中心值和左、右宽度的均值数据见表1：

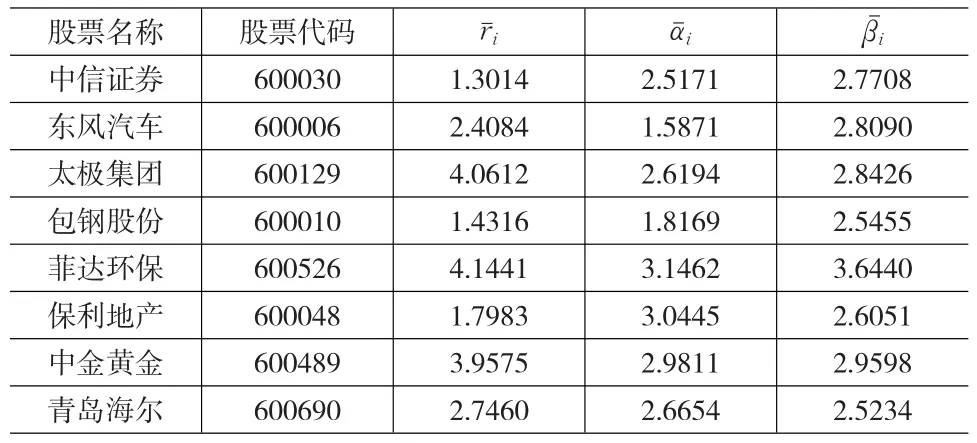
表1 8种证券的模糊收益率的中心及宽度数据表

根据投资者对不同股票的未来收益的不同偏好，可将λ取不同的值，从而可得到模糊收益率不同的加权可能性均值、加权可能性方差和加权可能性协方差。本文假设投资者的风险态度分别为比较乐观和比较悲观，分别取乐观系数为λ=0.6和λ=0.4，根据表1中的收益率数据和加权可能性均值、加权可能性方差和加权可能性协方差的定义求得对应不同风险乐观系数λ值的不同的加权可能性均值、加权可能性方差和加权可能性协方差阵。

当投资者的乐观系数λ=0.6时，八种证券模糊收益率的加权可能性均值见表2：

表2 乐观系数为0.6时8种证券模糊收益率的加权可能性均值表

当投资者的乐观系数λ=0.6时，八种证券的模糊收益率的加权可能性协方差阵见表3：

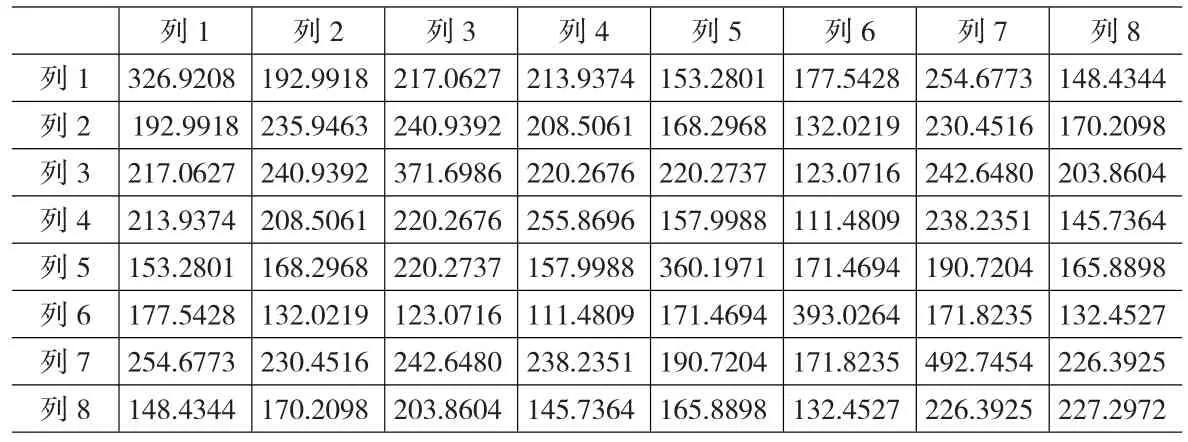
表3 乐观系数为0.6时8种证券模糊收益率的加权可能性协方差表

将表2和表3中的数据代入到模型（1），用Matlab软件可求得对应于不同的预期收益率下限的取值，相应的投资比例及风险见表4：

当投资者的乐观系数λ=0.4时，同理可以求出八种证券模糊收益率的加权可能性均值与可能性方差、协方差值，将其带入到模型（1）中，用Matlab软件可求得对应于不同的预期收益率下限的取值，相应的投资比例及风险见表5：

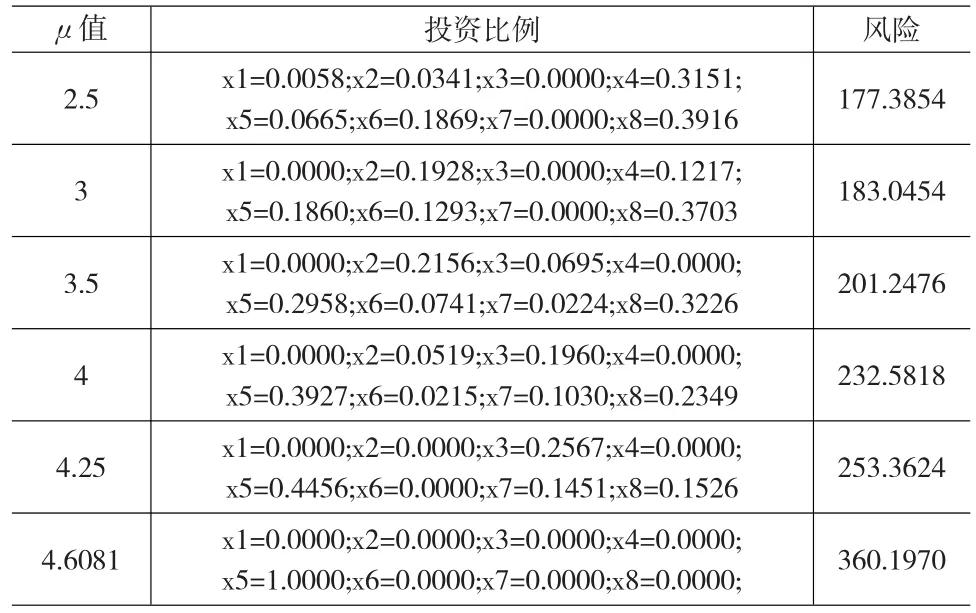
表4 乐观系数为0.6时加权可能性均值-方差模型的投资比例与风险表

表5 乐观系数为0.4时加权可能性均值-方差的模型的投资比例与风险表

从表4和表5可以看出，随着预期收益率下限的提高，两个模型的风险值都随之增大。但是对应于不同的λ值，虽然对于同样一个预期收益率的下限水平，投资者不同乐观系数的模型对应着投资比例和风险不同。例如当λ=0.6时，给定预期收益率下限为μ=3%时，投资比例为x1=0.0000;x2=0.1928;x3=0.0000;x4=0.1217;x5=0.1860;x6=0.1293;x7=0.0000;x8=0.3703，此时风险值为 183.0454；当λ=0.4时，给定预期收益率下限为μ=3%时，投资者的投资比例为x1=0.0000;x2=0.2323;x3=0.0816;x4=0.0000;x5=0.3021;x6=0.0562;x7=0.0312;x8=0.2967,此时风险值为201.9734。可见，投资者对未来收益的乐观态度不同会导致其在不同资产上的投资比例不同，乐观的投资者对未来收益的风险预期更小。

4 加权可能性均值-方差模型与Markowitz均值-方差模型的比较分析

对比加权可能性均值-方差的组合投资模型（1）和Markowitz均值-方差模型

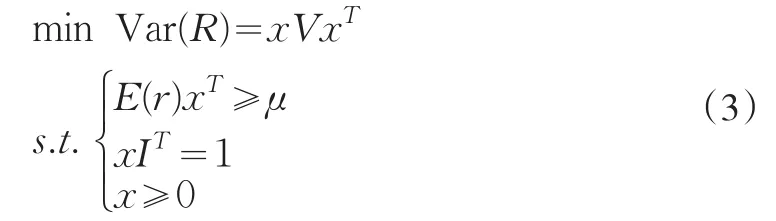
会发现两个模型的建模思想一致，都是在事先给定预期收益率下限的情况下，使投资者所承担风险最小化的问题。

可见本文的加权可能性均值是随机变量均值概念的推广，加权可能性方差和协方差分别是实数域中方差和协方差概念的推广。基于截集的加权可能性均值-方差的组合投资模型是传统的Markowitz均值-方差模型在随机变量取值为模糊数时的合理的推广，该模型将Markowitz均值-方差模型的思想推广到随机变量取值为模糊数时的组合投资问题中去，解决收益率为模糊数据时的组合投资决策问题。下面通过一个实例来说明两个模型在实际应用中的区别与联系。

为了便于模型间的比较，采用前文实证分析中的八种股票从2007年1月到2010年3月共39个月的月收益率数据，月收益率为

其中 pit末表示第i种股票第t个月最后一个交易日的收盘价格，pit初表示第i种股票第t个月第一个交易日的开盘价格。根据公式（4）求得八种股票的月收益率的均值数据和协方差阵，并将其带入到模型（3）中，可得不同预期收益率下限的不同的投资比例和风险值见表6。

为了更直观的描述加权可能性均值-方差模型与均值-方差模型的风险收益之间的对比关系，利用表4、表5和表6中的收益率和风险值数据画出三种模型的风险-收益关系图如下：

图1 不同风险乐观系数的加权可能性均值

从图1中可以看出，乐观系数为0.6的加权可能性模型的风险收益关系图在传统均值-方差模型的风险收益关系图的上方，乐观系数为0.4的加权可能性模型的风险收益关系图在传统均值-方差模型的风险收益关系图的下方。说明对应同一个预期收益率的下限，当决策者的乐观系数为0.6时，模型的风险值小于传统模型的风险值，当决策者的乐观系数为0.4时，模型的风险值大于传统模型的风险值。可见，三个模型的风险收益关系图的走向基本一致。当预期收益率的下限为3%时，三个模型都是将资金的大部分投资与股票2、股票5和股票8，投资比例略有细微的差别，但是差别不大。另外，三个模型所能到达的预期收益率的上限略有不同，乐观系数为0.6的加权可能性均值-方差组合投资模型所能达到的最高收益率水平为4.6081%，乐观系数为0.4的加权可能性均值-方差组合投资模型所能达到的最高收益率水平为3.929%，均值-方差模型所能达到的最高收益率水平为4.1441%。其原因在于投资者的风险乐观态度，投资者相对乐观时，即乐观系数较大时，其对股票的未来收益越偏向于模糊收益率的右端点，所以模糊收益率的均值越大，反之模糊收益率的均值越小。

5 结论

基于截集的加权可能性均值-方差的模型以随机变量取值为模糊数时的加权可能性均值和加权可能性方差为研究对象，类似于Markowitz均值-方差模型的思想构建了基于截集的加权可能性均值-方差组合投资决策模型。建模过程中考虑了投资者的主观意愿，投资者越回避风险，则对风险资产的未来收益的预期值越小；投资者越偏好风险，则对风险资产的未来收益的预期值越大，投资者可以通过选择风险乐观程度系数来体现自身的风险偏好。投资者的乐观系数小的模型风险收益关系图像位于乐观系数大的模型风险收益关系图的下方，说明对应于同一个收益率的下限，乐观系数较大的模型，风险值较小。这是因为乐观系数反映的是投资者对风险的认知态度，乐观系数越大，说明投资者对风险的态度越乐观，因此其对风险的描述值就较小；反之，乐观系数越小，说明投资者越谨慎，故其对风险值的描述就较大。因此乐观系数小的模型的风险值大于乐观系数大的模型的风险值，这与投资者对风险的认知态度有关系。实证分析还表明该模型是Markowitz均值-方差模型在随机变量的取值为模糊数时的一种合理推广，并且该模型比Markowitz均值-方差模型有着更加广泛的适用范围和应用前景。

[1]张卫国.现代投资组合理论——模型、方法与应用[M].北京：科学出版社,2007.

[2]陈炜,张润彤,杨玲.存在融资条件下证券组合选择的一种模糊决策方法[J].北京交通大学学报(社会科学版),2007,(3).

[3]付云鹏,马树才.一种新的基于可能性均值的证券组合投资决策模型[J].统计与决策，2011,（3）.

[4]林军,卢谦.模糊预期收益率下风险损失率的左偏差度量[J].模糊系统与数学,2003,(16).

[5]许若宁,翟晓燕.风险投资决策的模糊分析模型[J].模糊系统与数学,2008,（2）.