一种颗粒饲料PDI测试方法的研究

2013-02-20李倪薇康宏彬王红英

饲料工业 2013年19期

■高蕊李倪薇康宏彬王红英

(中国农业大学工学院农业部国家农产品加工技术装备研发分中心，北京 100083)

随着人们对动物肉类需求的不断加大，颗粒饲料作为动物赖以生存的物质基础，其质量一致性和加工技术成为饲料行业越来越关注的问题。颗粒饲料耐久性指数PDI(Pellet Durability Index)是评价饲料产品质量指标之一，其与颗粒饲料配方、粉料粒度、调质、压模和冷却等工艺息息相关。耐久性指数大，饲料的利用率高，对动物生长性能起到促进作用；PDI小，在运输途中易产生较多的粉尘，增加了饲料的损耗。美国堪萨斯州立大学最早研制出用回转箱法来模拟颗粒饲料在搬运过程中的损失，该方法取500 g颗粒料置于回转箱，振动旋转10 min，后过筛通过公式得到PDI值。K.K.Lundblad在原有测试的基础上，发明了一种修正PDI的测定方法，即在回转箱中加入五只13.0 mm六角形螺母；巴西农牧院Embrapa发明了MPE法，利用筛孔为4 mm的细筛，对300 g颗粒料进行振动筛分30 s，得到MPE值。英国Holmen设计了一种颗粒饲料耐久性的测定装置；John Payne经过研究，提出了有关常用配料对颗粒饲料制粒性能、制粒产量的影响，并将其以系数的方式进行了量化。但是美国堪萨斯州立大学的回转箱法测定颗粒耐久度用时长、用料多，不利于高效实验测定，而MPE原理简单，操作方便。但前人提出的MPE法，筛孔和筛分时间没有经过试验验证，普适性及代表性不强。所以本文结合中外学者的研究成果，进一步研究确定MPE法中筛孔的直径及筛分时间，从而得到对不同配方的颗粒饲料的MPE测定法；然后建立MPE与PDI的关系数学模型，从而利用该数学模型由MPE预测得到PDI值。

1 材料与方法

1.1 试验材料

试验所用颗粒饲料均取自农标普瑞纳（廊坊）饲料有限公司。每批取样3～5个，每个平行样品1.7 kg左右。共取得样品541个。具体颗粒料样品配方成分如下：

仔猪料：玉米39%、豆粕8%、乳清粉9%、进口鱼粉22%、次粉5%、奶粉5%、磷酸氢钙12%；

育肥猪：玉米66%、豆粕9%、麸皮10%、次粉12%、玉米蛋白粉2%；

妊娠母猪：玉米59%、豆粕8%、玉米蛋白饲料3%、麸皮19%、DDGS 8%、次粉5%；

4～60日龄犊牛料：玉米31%、豆粕22%、麸皮3%、次粉15%、玉米蛋白粉18%、DDGS 11%；

3～6月龄小牛颗粒饲料：玉米15%、豆粕6%、棉粕19%、次粉17%、玉米蛋白饲料19%。

1.2 试验仪器

回转箱(按照美国标准定制)；BZS-200标准检验筛机（新乡市同心机械有限责任公司）；电子精密天平（梅特勒-托利多仪器有限公司）。

1.3 试验方法

通过回转箱法和MPE法分别对颗粒饲料产品因碰撞、摩擦造成颗粒饲料的粉化程度进行测定，进而利用MPE法得到PDI的预测模型。

1.3.1 回转箱法

1.3.1.1 方法步骤

首先，在颗粒饲料打包过程中，随机称取5 kg颗粒饲料样品，将其置于表1规定的筛上进行筛分，筛去颗粒饲料中的粉状饲料，然后选取筛上物500 g装入回转箱内，盖好箱盖，启动粉化仪，使箱体运转10 min，停止后取出样品，再置于同一筛上筛分，称取筛上物得A，单位g。

表1 不同颗粒直径采用的筛孔尺寸

1.3.1.2 计算方法

PDI(%)=A/500×100。

所得结果精确至小数点后一位。两份样品测定结果绝对差不大于1%。

1.3.2 MPE法

MPE法是直接使用振动筛代替原来的回转箱，来模拟颗粒饲料的装卸、运输过程。MPE值为筛上物与筛前颗粒饲料质量的比值。

1.3.2.1 MPE法筛孔的确定

巴西农牧院Embrapa发明的MPE法，筛子孔径选取4 mm，但是不同的饲料，颗粒直径不同，所以该筛孔直径不能适用于所有粒径的颗粒饲料。由于MPE法是在试验过程中直接将样品进行筛分，而回转箱法是先振动后筛分，从本质上讲，选取筛孔直径的规律应当是相一致的。故本文将MPE法和回转箱法选取筛孔直径的标准相结合，仍选用表1的筛孔尺寸。

1.3.2.2 MPE法筛分时间的确定

试验选取3～6月小牛颗粒饲料和育肥猪颗粒饲料。3～6月小牛颗粒饲料经过了糖蜜后喷涂工艺，颗粒表面较致密，在运输过程中不易粉化；育肥猪颗粒饲料没有经过糖蜜后喷涂工艺，制粒方式为挤压制粒。图1为3～6月小牛颗粒饲料MPE值随振动时间变化曲线，图2为育肥猪颗粒饲料MPE值随振动时间变化曲线。

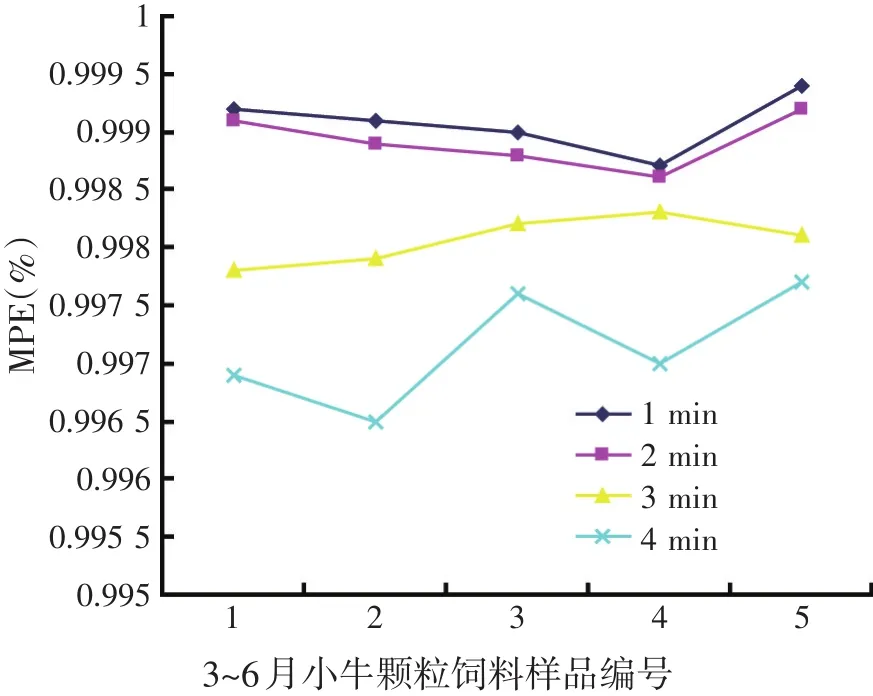
图1 3～6月小牛颗粒饲料MPE值随振动时间变化曲线

图2 育肥猪颗粒饲料MPE值随振动时间变化曲线

由图1及图2可以得出：3～6月小牛颗粒饲料和育肥猪颗料饲料振动时间为1～2 min，MPE值变化不大，说明在短时间、短距离的搬运对于颗粒饲料粉化程度没有太大的影响。为了更好地模拟搬运过程中颗粒饲料的粉化情况，故增加MPE法振筛时间。从图中可以看出，在振动时间设定在3、4 min时两种颗粒饲料MPE有明显的变化，所以振动时间确定在3～4 min之间。由图1可知，对于小牛料采用MPE方法振筛3 min与振筛4 min，其MPE值相差在0.000 4～0.001 8之间，MPE值相差很小。由图2可知，对于生长猪料采用MPE方法振筛3 min与振筛4 min，其MPE值相差0.01左右，相差也不大。因此可选用3 min或4 min作为MPE的振筛时间，相比传统PDI回转10 min的时间，MPE方法缩短了50%的测试时间。为更接近模拟长时间运输的情况，故选取4 min振动时间。

1.3.2.3 MPE法步骤

首先，在颗粒饲料打包过程中，称取5 kg颗粒饲料样品，将其置于表1规定的筛上进行筛分，筛去颗粒饲料中的粉状饲料，然后选取筛上物300 g左右样品，称重记为B，单位g，置于振动筛，在同一筛上进行筛分4 min，称取筛上物得C，单位g。

1.3.2.4 计算方法

式中：A——颗粒饲料样品质量(g)；

B——筛分后除去粉状饲料的颗粒饲料质量(g)。

2 结果与分析

2.1 试验结果（见表2）

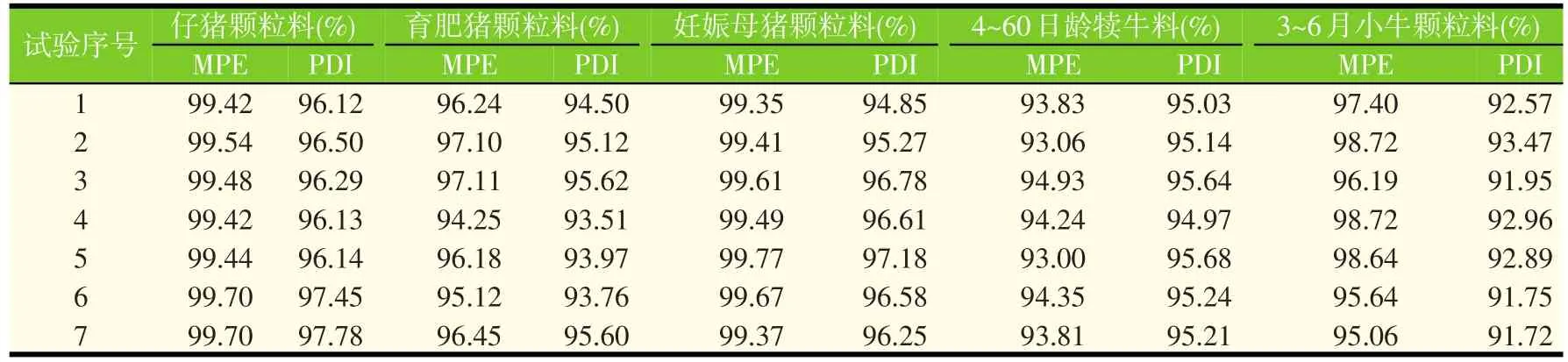
表2 颗粒饲料PDI、MPE试验结果

表2为仔猪料、育肥猪、妊娠母猪、4～60日龄犊牛、3～6月龄小牛的MPE、PDI测试结果，MPE的测试时间为4 min。

2.2 MPE与PDI相关性分析

本试验均在室温条件下完成，如图3所示，仔猪颗粒饲料PDI与MPE呈良好的线性关系，经数据回归得到方程PDI=-418.409+5.174MPE，相关系数R2=0.926。

采用SPSS17.0软件对仔猪颗粒饲料试验数据进行分析，运用ANOVA程序进行方差分析，结果如表3所示。

由图4可知，育肥猪颗粒饲料PDI与MPE呈良好的线性关系，经数据回归得到方程PDI=8.427+0.897MPE，相关系数R2=0.892。

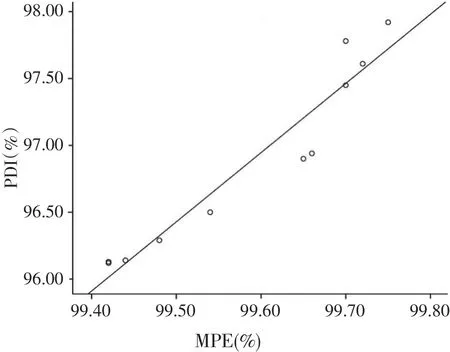
图3 仔猪颗粒饲料PDI与MPE相关性曲线

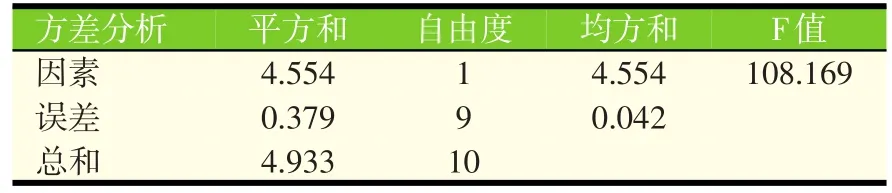
表3 仔猪颗粒饲料方差分析

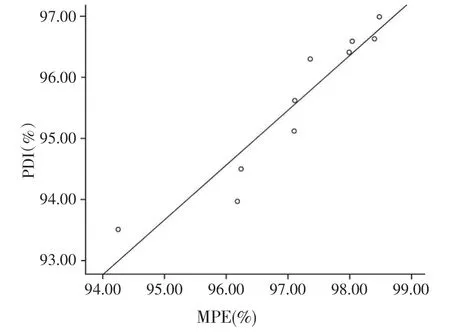
图4 育肥猪PDI与MPE相关性曲线

采用SPSS17.0软件对育肥猪颗粒饲料试验数据进行分析，运用ANOVA程序进行方差分析，结果如表4所示。

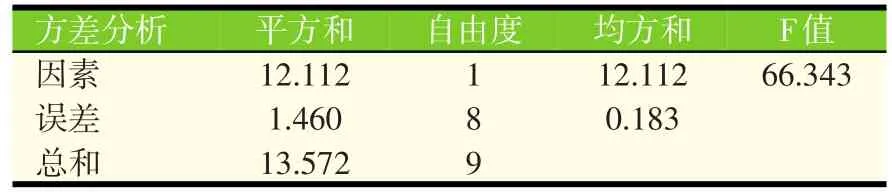
表4 育肥猪颗粒饲料方差分析

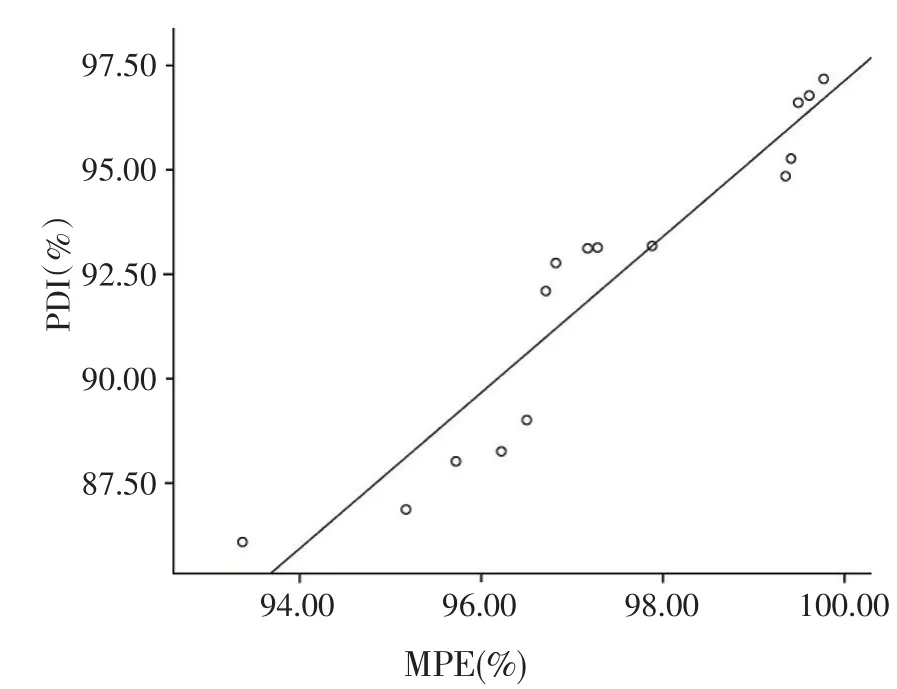
图5 妊娠猪颗粒饲料PDI与MPE相关性曲线

由图5可知，妊娠猪颗粒饲料PDI与MPE呈良好的线性关系，经数据回归得到方程PDI=-89.556+1.867MPE，相关系数R2=0.901。

采用SPSS17.0软件对妊娠猪颗粒饲料试验数据进行分析，运用ANOVA程序进行方差分析，结果如表5所示。

表5 妊娠猪颗粒饲料方差分析

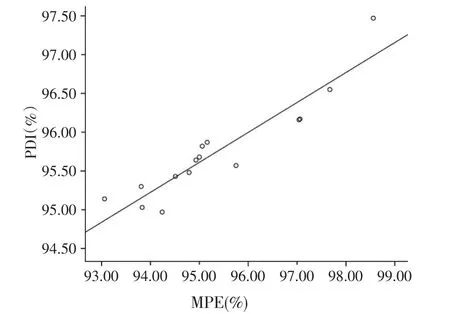
图6 4～60日龄犊牛颗粒饲料PDI与MPE相关性曲线

由图6可知，4～60日龄犊牛料PDI与MPE呈良好的线性关系，经数据回归得到方程PDI=58.928+0.386MPE，相关系数R2=0.867。

采用SPSS17.0软件对4～60日龄犊牛颗粒饲料试验数据进行分析，运用ANOVA程序进行方差分析，结果如表6所示。

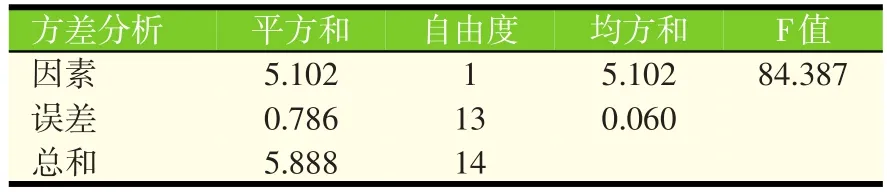
表6 4～60日龄犊牛颗粒饲料方差分析

由图7可知，3～6月龄小牛颗粒饲料PDI与MPE呈良好的线性关系，经数据回归得到方程PDI=18.762+0.762MPE，相关系数R2=0.848。

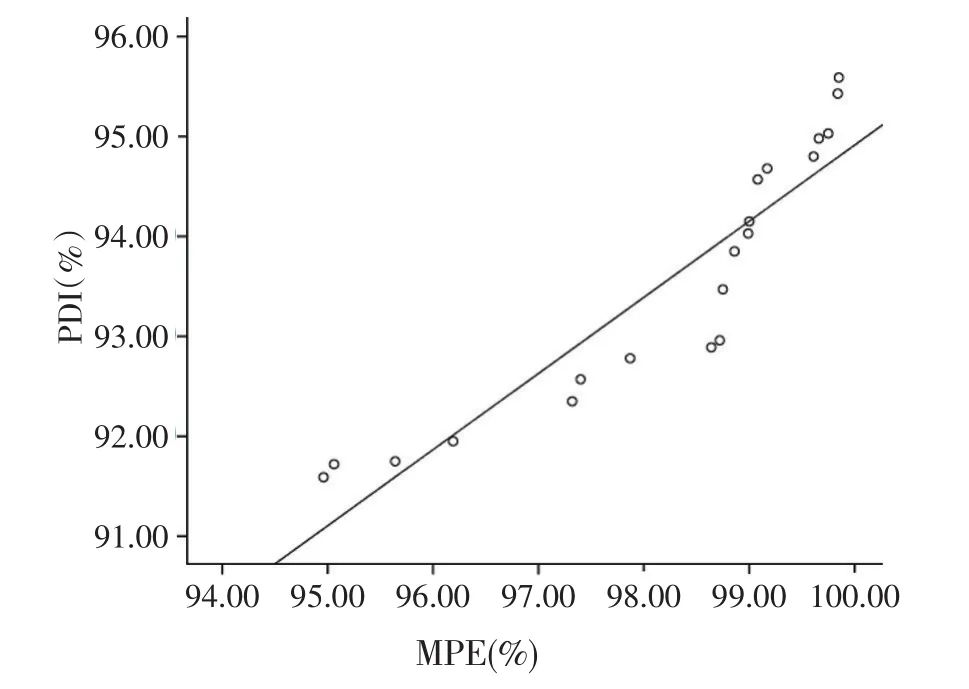
图7 3～6月龄小牛料PDI与MPE相关性曲线

采用SPSS17.0软件对3～6月龄小牛颗粒饲料试验数据进行分析，运用ANOVA程序进行方差分析，结果如表7所示。

表7 3～6月龄小牛料方差分析

为了验证猪、牛颗粒饲料的MPE与PDI相关性模型的建立是否适合，本文以普瑞纳生产的猪、牛颗粒饲料进行实验验证。根据企业生产的产品品种，选取仔猪颗粒饲料、育肥猪颗粒饲料、妊娠母猪、4～60日龄犊牛料、3～6月龄小牛颗粒饲料，每种选取8个平行样品进行验证试验。根据这5种颗粒饲料的MPE和PDI相关性模型预测PDI的值，将模型PDI预测值与PDI实际测得值进行回归分析。结果表明PDI预测值与PDI实际测得值相近，在置信区间为95%的条件下，R2＞0.96，预测效果显著。