双馈式风电变流器低电压穿越技术的研究

沈友朋，骆 皓，肖 遥，庄 俊

(国电南京自动化股份有限公司，江苏 南京210003)

0 引言

目前，风力发电机组装机容量越来越大，并网机组也随之增多，风电并网对电网安全的影响也越来越重要。因此，要求并网的风机必须具备很强的故障穿越能力。而风电变流器作为风力发电并网系统的关键部分，因此也应该具备故障穿越能力。所以研究风电变流器低电压穿越技术对提高风电接入电网的友好性及电网安全有重要的现实意义。为此本文对双馈式风电变流器低电压穿越技术进行了相关的研究和分析。文献［1，2］只对电网电压三相平衡跌落时的低电压穿越技术进行了研究。文献［3 ～5］对电网电压不平衡跌落时风电变流器低电压穿越的控制进行了研究。本文提出分别在电网电压三相平衡和单相不平衡跌落时低电压穿越的控制策略。

1 电网平衡跌落条件下的DFIG 控制策

1.1 转子侧变换器控制策略

对于转子侧而言，其控制的目的是为了实现发电机有功和无功的解耦。该控制目标可以通过分别对转子电流有功和无功分量的控制来实现。

一般在电网电压平衡跌落下转子侧变换器的功率方程［3］为

式中:Ps代表有功功率;Qs代表无功功率;Usd代表dq 坐标系下的定子电压，irq，ird分别代表dq 坐标系下的q 轴和d 轴转子电流，Ls，Lm分别代表dq 坐标系下的定子自感和dq 坐标系下定、转子之间的互感;ωs代表同步电角速度。

从上式可看出，转子电流的有功分量ird可以控制定子输出的有功功率，无功分量irq可以控制定子输出的无功功率。若调节ird而不会影响irq，反之亦然。这样就可以通过控制其有功分量ird和无功分量irq来实现有功和无功功率的解耦控制。

1.2 网侧变换器控制策略

对于DFIG 而言其直流母线电容电压的稳定是DFIG 稳定运行的前提，当电网发生故障时，会引起母线电容电压的波动，从而影响转子侧和网侧变换器的正常工作，而保持直流电压的稳定是通过控制网侧变换器来实现的。

网侧变换器的控制一般采用电压定向的控制方式来实现直流电压的稳定。在电压定向的条件下，网侧变换器的dq 分量可用下式来表示［3］:

式中:Vdc为直流侧电压;Ugd为电网电压的d 轴分量;Rg为网侧进线电抗器电阻;igd，igq分别为网侧电流的d 轴、q 轴分量;Lg为网侧进线电抗器电感;Sd，Sq分别为开关函数的d 轴、q 轴分量;ωs为同步电角速度。

在式(2)中，若令:

在式(3)中为了消除静差，引入积分环节可得网侧变换器的电流控制器:

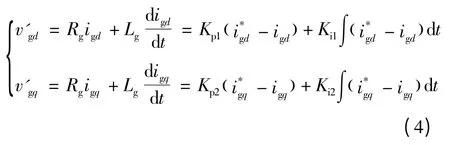
同理可得直流环节电压调节器为

由式(2) ～ (5)可知网侧变换器的控制指令为

因此，网侧变换器是通过对电流调节器和电压调节器的控制来实现直流侧稳压的。同时为了保证输出功率因数为1，一般将电流无功分量的给定值irq*为0，故其交流侧输入的无功功率为0。

2 电网不平衡跌落条件下的DFIG控制

2.1 转子侧变换器控制策略

当电网电压发生不平衡跌落时，其电压和电流不仅含有正序分量，还存在负序分量。而负序分量的存在对定、转子电流有很大影响，会造成电流的高度不平衡，同时使发电机电磁转矩发生脉动。因此，可以通过抑制电磁转矩脉动来减小该影响。

对于转子侧变换器，当发生不平衡跌落时，其定、转子电流、电压和磁链可表示为正负序分量的组合［4］:

式中:F 为电压、电流或磁链;+，－表示正负序旋转参考坐标。

转子侧的电压方程可由下式表示:

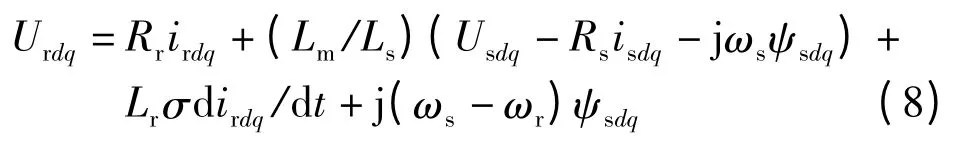
式中:Usdq，Urdq分别为dq 坐标系下的定、转子电压;Rs，Rr分别为定、转子电阻;isdq，irdq分别为dq 坐标系下的定、转子电流;Ls，Lr分别为定、转子自感，Ls=Lσs+Lm，Lr=Lσr+Lm，Lσs，Lσr分别为定、转子漏感;Lm为定、转子间互感;ωs－ωr为相对角速度;σ 为漏感系数，σ = 1 －/(LsLr)。

可将式(7)代入上式得:

2.2 网侧变换器控制策略

网侧变换器的控制目标是稳定直流母线电压，并在需要时能为电网提供无功补偿。当电网电压发生不平衡跌落时，产生的负序分量会使直流环节发生严重的过压情况。因此，对网侧变换器的控制是为了限制直流环节的过压，故对网侧变换器采取抑制交流侧负序电流的控制策略。一般令负序电流给定值==0，为了得到单位功率因数，一般令无功功率平均值Q0=0，其直流侧有功功率平均值P0与直流电压有关，也即:

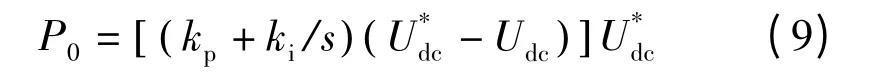
式中:kp，ki为PI 调节参数;s 为开关函数;，Udc分别为直流侧电压给定值和实际直流电压。

而正序电流给定值为

3 系统仿真研究

为了验证电网电压发生平衡和不平衡跌落时，上述转子侧和网侧变换器控制策略的正确性和可行性，建立了如图1 所示的DFIG 系统模型图。系统仿真参数为:P =1.5 MW，U =690 V，fg=50 Hz，Rs=0.000 7 p．u．，Rr=0.005 p．u．，L1s=0.17 p．u．，L1r=0.156 p．u．，Lm=2.9 p．u．，Jm=0.685 s，np=3。

图1 DFIG 风力发电系统模型结构图Fig．1 Model diagram of DFIG wind power system

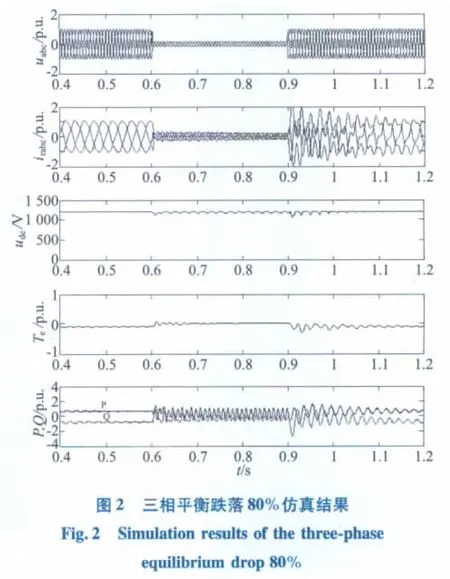
分别对电网电压发生三相平衡跌落和单相不平衡跌落时转子电流irabc、直流电压udc、电磁转矩Te和有功无功P，Q 进行仿真。仿真条件均为0.6 s 电网电压发生跌落，0.9 s 故障解除。

图2 为当电网发生严重的三相平衡跌落时采用上述控制策略时的仿真结果。从图中可看出其转子电流在故障期间和故障解除瞬间对电网的冲击不是很大，同时也可有效地抑制电磁转矩和直流电压的波动。

图3 为当电网A 相电压发生严重跌落时采取上述控制策略的仿真结果。从图中可看出，若跌落时不采取其他措施，转子电流会存在严重的2倍频分量，这会严重冲击电网。直流电压和电磁转矩也存在一定的波动。这说明当电网发生严重不平衡跌落时，只采用上述控制策略，是不能满足变流器在电网故障期间的低电压穿越能力，且对电网会产生严重的冲击。

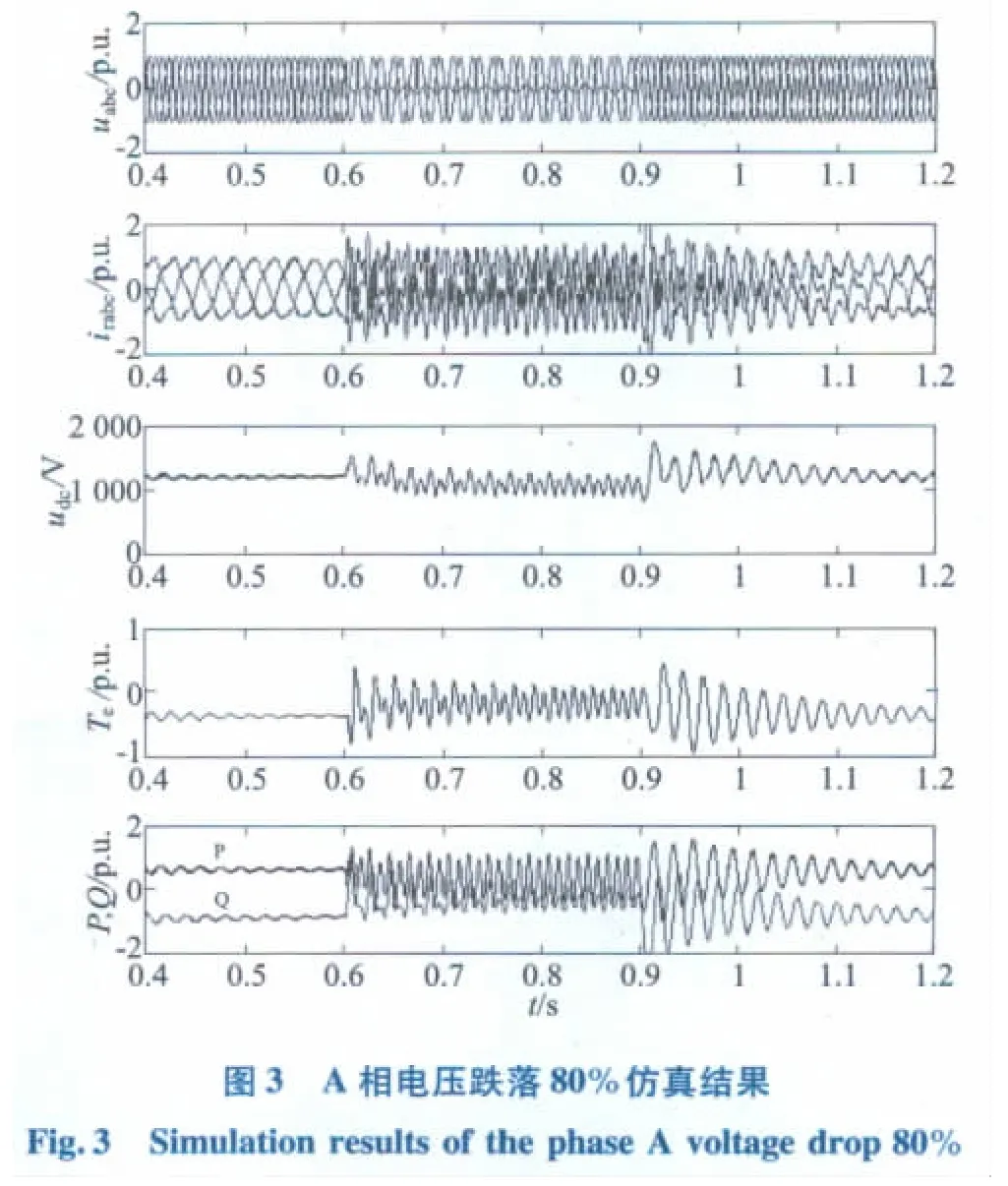
为了保证当电网发生严重不平衡跌落时变流器的低电压穿越能力，一般会在转子侧变换器和直流电容侧加硬件电路——也称Crowbar 电路，以减小其对电网的冲击。图4 为A 相电压跌落80%加入Crowbar 电路时的仿真结果。由图4 可知，当加入Crowbar 电路后，可很好地抑制转子电流的2 倍频分量，同时也大大减小了直流电压和电磁转矩的波动。

图4 A 相电压跌落80%加入Crowbar 电路仿真结果Fig．4 Simulation results of phase A voltage drop 80%added to the Crowbar circuit

4 结论

仿真结果表明，当发生严重三相平衡跌落时，采取本文介绍的控制策略可很好地保证变流器在电网故障期间的低电压穿越能力;而当发生严重的不平衡跌落时，只采用本文介绍的控制策略是不能保证其低电压穿越能力，而且会对电网产生很大的冲击。因此，当电网发生严重不平衡跌落时，必须要加入Crowbar电路，以保证变流器在故障期间的低电压穿越能力。有关于Crowbar 电路是否能很好地解决平衡跌落的问题，本文将进一步进行研究。

［1］张学广，徐殿国．电网对称故障下基于active crowbar 双馈发电机控制［J］．电机与控制学报，2009，13 (1):99-103．Zhang Xueguang，Xu Dianguo．Reseach on control of DFIG with active crowbar under symmetry voltage fault condition［J］．Electric Machines and Control，2009，13 (1):99-103．

［2］马文龙．Crowbar 保护在双馈异步风电发电系统电网故障穿越中的应用［J］．电力自动化设备，2011，31(7):127-130．Ma Wenlong．Application of Crowbar circuit in grid fault riding for doubly-fed induction wind power generation system［J］．Electic Power Autonmation Equipment，2011，31(7):127-130．

［3］Xu L，Wang Y．Dynamic modeling and control of DFIG based wind turines under unbalanced network conditions［J］．IEEE Trans．on Power Systems，2007，22 (1):314-323．

［4］Patrick S Flannery，Giri Venkataramanan．A fault tolerant doubly fed induction generator wind turbine using a paralled grid side rectifier and series grid converter ［J］．IEEE Trans．on Power Sytems，2008，23 (3):1126-1135．

［5］Yan Xiangwu，Giri Venkataramannan，Patrick S Flannery，et al．Voltage-sag tolerance of DFIG wind turbine with a series grid side passive-impedance network ［J］．IEEE Trans．on Power Systems，2010，25 (4):1048-1056．