中职数学建模活动中创新思维研究

韩顺龙

（重庆市护士学校 重庆401320）

按照现行高中阶段数学课程目标的教学要求，结合医疗卫生行业的特点，中职学校开设数学课是为了帮助学生进行专业课学习和适应今后临床工作的需要。对护理临床及生活中问题调查发现，数学模型的构建及计算已成为中职学生就业前应该而必须获取的技能。针对近几年的毕业生就业跟踪调查表明，模型构建技能较好的学生思维更有创造性，更能解决生活和工作中出现的问题，更受用人单位的欢迎。在中职数学教学中采用题型加方法的教学模式，能在某种程度上提升学生的感知能力。在教学中，常常发现学生遇到未见过的题型时不知道用怎样的数学方法解决，常常倾向于否定自己，归因于数学难学；特别是遇到与实际联系紧密的问题时更是束手无策，一筹莫展。这既表明他们数学思维的缺乏，也体现出曾经数学教学的失败。学生从小学一年级就开始学习数学，但相当一部分学生仍缺乏基本的数学思维，接触实际问题越多，该现象表现越突出。如果仍采取原有教学模式，培养学生的数学能力只能是一句空话。笔者认为，建模实践活动不失为一剂良方。

构建数学模型的必要性及过程

以我们生活中某一问题为研究对象，对该问题做一些必要的假设，用恰当的数学工具和数学语言来表述一个数学结构，这个结构即为数学模型，其中数学概念、公式或方程、定理等结构体系是构建数学模型的基础。归纳前人构建数学模型解决实际问题的过程和思维方式，其过程大致如图1所示。

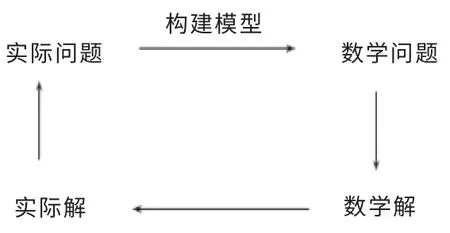
图1 建模构建思路图

在这个过程中，把实际问题变成数学问题是用数学建模解决实际问题的关键，这是学生能力的体现。因为学生要通过对实际问题观察和分析、构架模型，用数学思维方法表述它们的关系和相关信息，用熟悉的数学模型来表达，从而使实际问题在数学模型框架内得到解决。

在数学实践教学活动中，以专业为导向，学生为主体，有针对性地开展模型构建活动是十分必要的。按照现行中职学校数学课程教学目标，数学要为学生专业课程的学习提供服务，用数学的思维架构（即模型）和方法解决（或解释）专业课程学习中遇到的问题；在学习、生活或工作中增强数学应用意识，能有机地把数学模型与实际问题较好地结合起来；在解决问题的过程中引导学生体验探测与判断，运算与证明等数学方法带来的快感。在中职学生中有针对性地开展数学建模活动，以提升学生思维能力为目标，引导学生自觉地运用数学知识和方法解决实际问题，智能型的劳动者将会在他们中产生，这时的智能型是指具有探索新知识，创造性地用新方法解决问题的能力。

在新生入学的第一堂课，我面对全班学生展示了头孢菌素（先锋霉素）皮试溶液的配制过程：首先，取头孢菌素0.5g加生理盐水5ml溶解摇匀；然后，抽取0.lml稀释至5ml后摇匀；再抽取0.15ml稀释至5ml摇匀即成（每毫升含头孢菌素60ug）；最后，要求学生分析该过程药量的变化关系，提示学生解决该问题的关键是构建单位体积量模型：

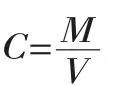
其中C表示单位体积量，M表示质量，V表示体积。

用模型计算：

首先，取头孢菌素0.5g加生理盐水5ml溶解摇匀，溶液单位体积量；

此时，最终的单位体积量C3=60ug。即为配制的皮试液。

这是一个和学生临床联系十分紧密的问题，把它和数学建模实践活动结合起来，既增长了数学知识，又激发了学习兴趣，有利于学生建模意识的形成。

建模活动过程中创新思维实现的基本途径

让建模走入现实生活，在现实生活中培养创新思维意识。比如，生活中常用的信用贷款问题，若把这个问题引入教学实践中，教学内容会更加丰富而生动，数学建模活动更富有内涵。在建模活动中渗透建模意识，同时，也领悟数学建模的广泛应用，进而激发学生参与数学建模实践活动的兴趣，可提升学生会用数学知识进行建模的能力。

把数学知识的获取与相关课程联系起来，丰富建模内容及方法。如数学模型：

y=Asin（ωx+θ）

在数学教学内容中它是正弦型函数，若用物理学中的振动问题或临床中的相关生命特征图进行比较学习，这样的模型不仅可以让抽象的数学知识更加具体，而且将会对学生学习相关学科产生深远的影响。用正弦型函数图像进行生命特征数据直（曲）线拟合建模专题讨论，通过讨论和分析，体验建模思想，熟悉建模方法，让学生尝到建模成功带来的快感。

建模活动中创新思维的基本方法

创新思维的根本点是灵感，具体表现为直觉、转换、构造三种方法。它是创新思维所具有的特征。

直觉产生灵感，用数学模型解决数学问题。像二项式定理、正弦定理、勾股定理等，是人类在生活实践中，通过观测、比较、感悟等直觉方式、突发灵感而发现的。比如求下列三角函式的值：

sin5°+sin77°+sin149°+sin221°+sin293°

指导学生先从表达式中角的数量特征来看，发现这些角都依次相差72°，再联想到正五边形的内角关系，由此构造一个与正五边形相关的几何模型（见图2），观察发现表达式的值刚好是在y轴上的分量之和，且这五个向量刚好构成一个封闭的正五边形（即向量和为0），它们的各个向量在y轴上的分量之和等于0。因此，所求三角函数式的值为0。

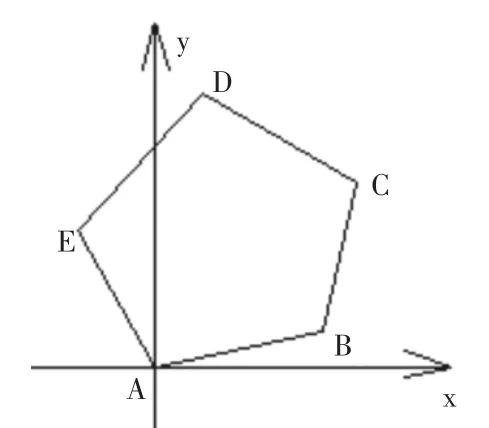
图2 三角函数值正五边形建模图

转换孕育创新思维，有了这样的思维才能实现问题向数学模型的转换。问题的表现形式是多样的，由一种形式向另一种形式转化过程中寻求解决，如果没有它，问题的解决难以突破。在数学教学中，把实际问题转换成数学问题，这个过程就是创新思维的体现。比如在静脉输液中，静脉点滴是临床给药途径之一，在单位时间内给一定量的液体、药物，对治疗疾病的效果起着一定的作用。为了方便操作，在临床上通常以15滴为1ml估算，快速估算每分钟滴数或每小时输液量，对每个患者的输液速度做到心中有数。引导学生构建如下数学模型：

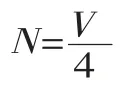
其中，N表示每分钟滴数，每小时输入量记为Vml，V∈（0，+∞）。在临床上某病人1小时内输液200ml，由构建的数学模型方便地估算出输液速度为每分钟需滴50滴。输液速度过快可能引起肺水肿，过慢会影响治疗时机，故在治疗中应酌情掌握。常规补液速度：小儿每公斤体重为1滴／分，成人每分钟60滴为宜，不得超过90滴。学生对这个将来在临床上要遇到的问题进行转换，无疑会激发其学习数学的主动性。

构造是创新思维的载体，培养学生创新思维能力的核心就是构造力。直觉中包含了构造力，转换中也包含了构造力。教师在引导学生构造数学模型时，要精心设计、仔细观察，让抽象的问题回归到熟悉的数学模型，实现问题到模型的跨跃。

在中职数学教学实践中围绕专业特色开展学生的数学建模活动，它与专业课教学要求培养学生创新思维能力是一致的。培养学生的创新能力，在教学中坚持以学生为主体，针对专业课程学习或学生实际开展建模教学活动，引导学生自主活动，自觉学习。只有这样，才能真正提高学生的创新能力，实现培养目标。

[1]（美）Mark M.Meerschaert.数学建模方法与分析（第3版）[M].刘来福，杨淳，黄海洋，译.北京：机械工业出版社，2009.

[2]沈文选，杨清桃.数学建模引导[M].哈尔滨：哈尔滨工业大学出版社，2008.

[3]李小寒，尚少梅.基础护理学[M].北京：人民卫生出版社，2006.

[4]郑成生.中职数学教学现状分析与对策[J].职业技术教育，2010（32）.

[5]叶家兴，施国亮.中职数学校本教材现状的分析与思考[J].中等职业教育，2009（32）.