基于不确定性的线路退运模糊潮流计算

李晖，潘旭东，刘涤尘，吴军，赵一婕，董飞飞

(1.国网北京经济技术研究院，北京市100052;2.武汉大学电气工程学院，武汉市430072)

0 引言

近年来，电网连锁故障导致的大规模停电事故在世界范围内频繁发生，造成了巨大的经济损失和严重的社会影响。因此，对不同线路的重要性进行评估，有效识别出重要线路并加强该区域的网架结构建设，对于提高电网的可靠性及避免造成大区域停电具有重要的意义。线路的重要性评估，可采用“单一线路退运后对系统造成的危害程度”这一标准，选取低电压以及过负荷为指标，根据单一线路退运后系统运行状态的变化来进行比选。电力系统作为典型的复杂、非线性系统，涉及许多不确定性因素，发电机出力、节点负荷很难被准确地确定，从而导致潮流分布不确定，因此，在进行线路退运后系统状态的分析时有必要考虑这些不确定性因素。

文献［1-2］采用区间分析方法来处理潮流计算中的不确定性因素，并进行了线路开断后的分析，但是此方法只是应用在直流潮流计算中，并不能反映线路开断后各节点电压的变化。文献［3］介绍了一种分析支路断线的概率潮流方法，其对于负荷、发电机出力的不确定性均假设其服从某一分布函数，带有较强的主观性。

本文的主要目的是研究模糊理论在线路退运分析过程中不确定性处理的应用问题。应用模糊集理论中的梯形模糊数描述发电机出力、发电机可用度及预测负荷的不确定性，在前人研究计及不确定性的模糊潮流计算方法的基础上，结合线路开断的快速模拟算法中的灵敏度分析法，提出计及不确定性的线路退运后的模糊潮流算法。

1 发电机出力、发电机可用度及负荷不确定性的模糊描述

电力系统中的一些不确定性变量具有模糊特性，宜用模糊集合论中的模糊数描述［4-5］。当引入模糊集合论后，潮流计算中的一些运算将转化为模糊数之间的运算。有关模糊数的定义及其运算见文献［6］。

在模糊潮流计算中，发电机出力、发电机可用度以及负荷的不确定性可采用三角模糊数［7］或者梯形模糊数［8-9］表示。本文采用梯形模糊数描述，以负荷为例，某节点负荷的预测值可能出现在L1～L4之间，而最可能出现在L2～L3之间，负荷的这种不确定性可采用一个如图1所示的梯形模糊数L4)表示，其隶属函数为

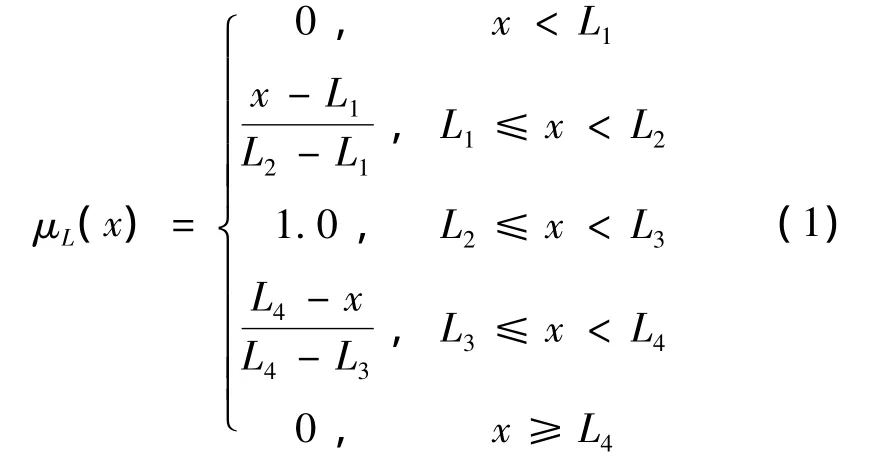
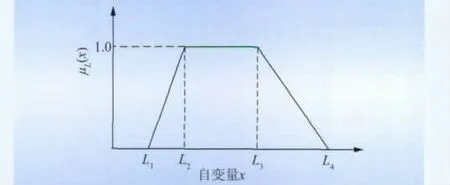
图1 梯形模糊数Fig.1 Trapezoidal fuzzy numbers

模糊数中心值为 μL(x)=1.0截集的平均值

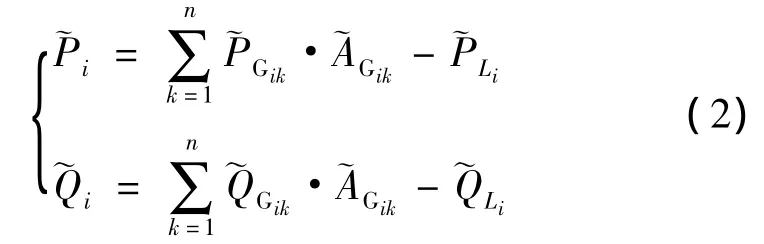
式中n为i节点上的发电机台数。由模糊数的运算可知，~Pi、~Qi也是梯形模糊数。

2 线路开断的灵敏度分析法

线路开断的灵敏度分析法方法是将线路开断视为正常运行情况的一种扰动，从电力系统潮流方程的泰勒级数展开式出发，导出了灵敏度矩阵，以节点注入功率的增量模拟断线的影响，较好地解决了电力系统断线分析计算的问题［10-12］。

根据牛顿潮流修正方程式:

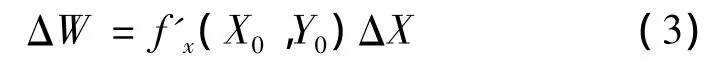
式中:X0为状态变量;Y0为网络参数;f'x(X0，Y0)为雅可比矩阵;ΔW为节点不平衡功率。于是有

其中

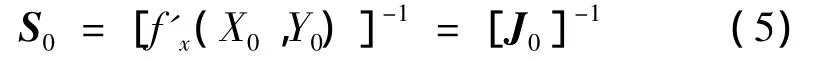
式中:S0为灵敏度矩阵;J0是牛顿潮流法中的雅可比矩阵。由于潮流计算中雅可比矩阵已经进行了三角分解，所以S0可以由回代过程求出。

若系统注入功率发生扰动为ΔW，或网络发生变化ΔY，状态变量也必然会出现变化，设其变化量为ΔX，并满足方程

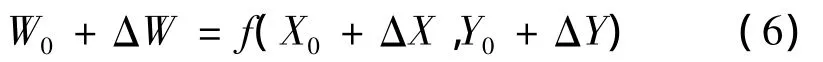
将上式按泰勒级数展开，忽略(ΔX)2项及高次项，且f(X，Y)是Y的线性参数，故f″yy(X，Y)=0，当不考虑节点注入功率的扰动时，ΔW=0，化简可得到

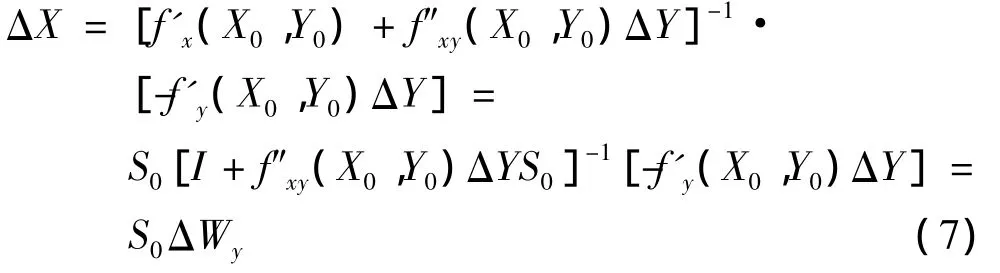
式中:I为单位矩阵;ΔWy可看成是支路开断而引起的注入功率扰动。

本文仅考虑单条线路开断的情况。假设开断的支路两端的节点i和j通过推导，最终写成矩阵的形式为

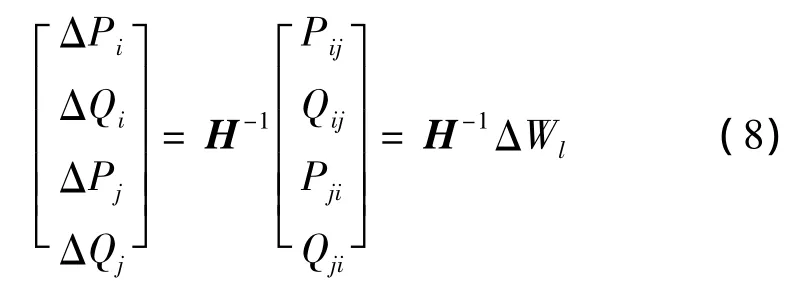
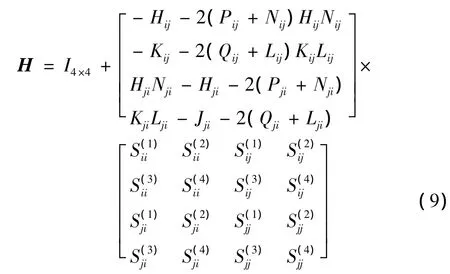
式中:ΔPi、ΔQi、ΔPj、ΔQj为开断线路 i、j时等效节点的注入功率均为灵敏度矩阵中行与列与断线端点i、j有关的元素。

3 单一线路退运后的模糊潮流计算

本文在断线分析的灵敏度法的基础上，考虑不确定性因素的影响，提出了线路退运后的模糊潮流算法。由于利用灵敏度分析法进行断线计算时，在求取断线处的节点注入功率增量时所用到的H矩阵和潮流功率均与正常运行情况下的潮流计算有关，因此采用改进的增量法以求取线路退运后的模糊潮流计算(此处假设所断线路两端节点为P、Q节点)，其计算流程图如图2所示。

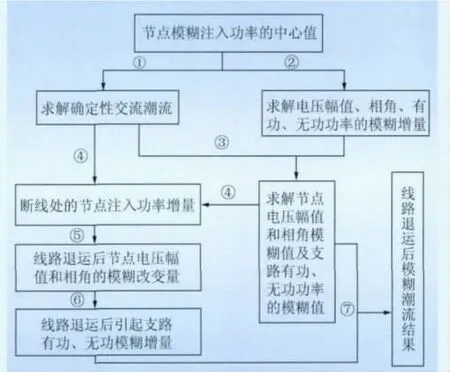
图2 线路退运的模糊潮流计算方法流程Fig.2 Flowchart of fuzzy load flow calculation after line returned

其计算步骤如下:

(2)由增量法求解正常情况下电压幅值、相角以及有功、无功功率的模糊增量。

采用牛顿－拉夫逊潮流算法时，可得

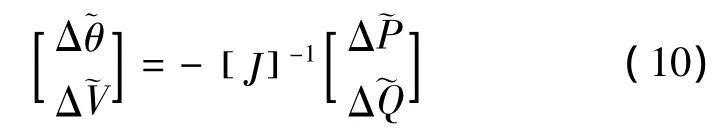
式中，雅可比矩阵[J]为确定性潮流计算时的最后一次迭代值。

已知支路的潮流方程为

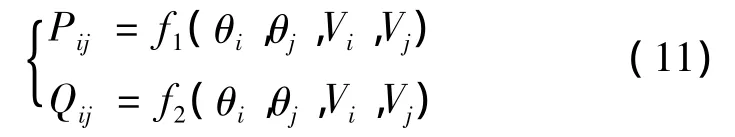
将其在某一运行点处(即中心点处)线性化，利用忽略二阶及以上项的泰勒级数展开式，并考虑状态变量增量的模糊性，则有

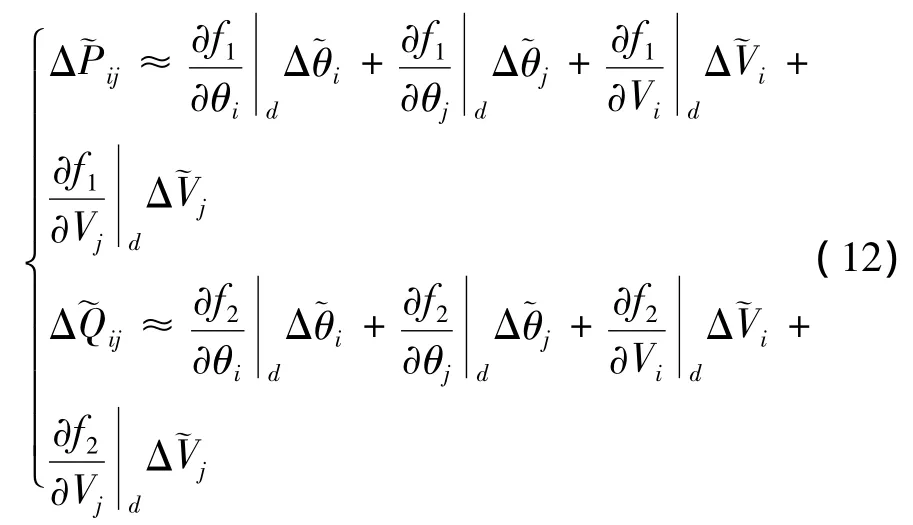
(4)利用节点模糊注入功率［~P］、［~Q］的中心值求取交流潮流方程时的最后一次迭代的雅可比矩阵中的元素来形成H矩阵，并利用步骤(3)中得到的有功、无功功率的梯形模糊数来形成ΔWl矩阵，于是，断线处的节点注入功率增量可表示为

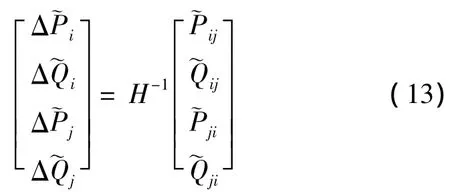
(5)根据断线处的节点注入功率梯形模糊数求取线路开断后引起的各节点电压幅值和相角的模糊改变量，可由修正方程式求出。

(7)利用模糊数的运算法则，将正常运行下所求得的模糊潮流结果与线路退运后求得的节点电压幅值、相角和有功、无功模糊增量进行叠加，进而可求出计及不确定性线路退运后各节点的电压幅值和相角以及各支路有功功率、无功功率的梯形模糊数。

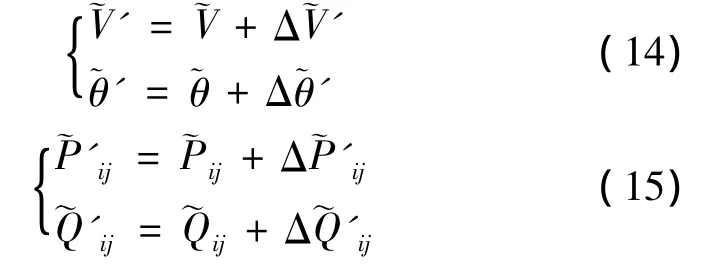
4 算例分析

利用本文研究的算法对IEEE－30节点系统进行线路退运后的模糊潮流计算。本算例中，模糊负荷及发电机模糊出力用梯形模糊数表示，其中对应μ(x)=0及μ(x)=1截集的极端值取为相应的中心值的(0.9，0.95，1.05，1.1)倍。基准容量 SB=100 MVA。

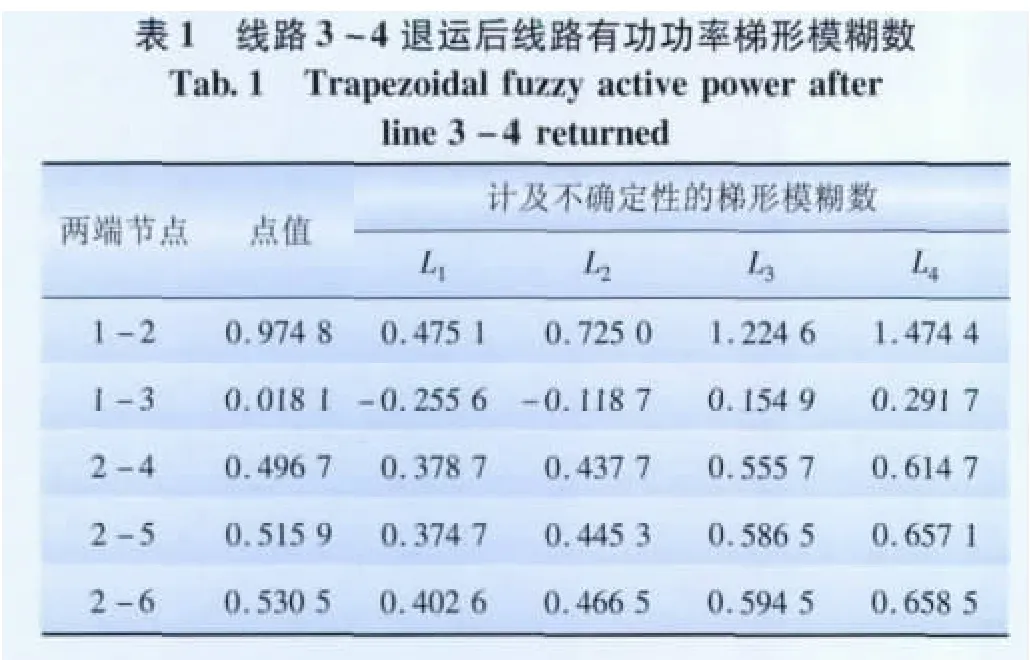
以线路3－4退运为例，由于篇幅所限，表1给出了部分计算结果。图3、4分别给出了线路3－4退运后节点3的电压梯形模糊图以及线路2－6有功功率梯形模糊图。

?

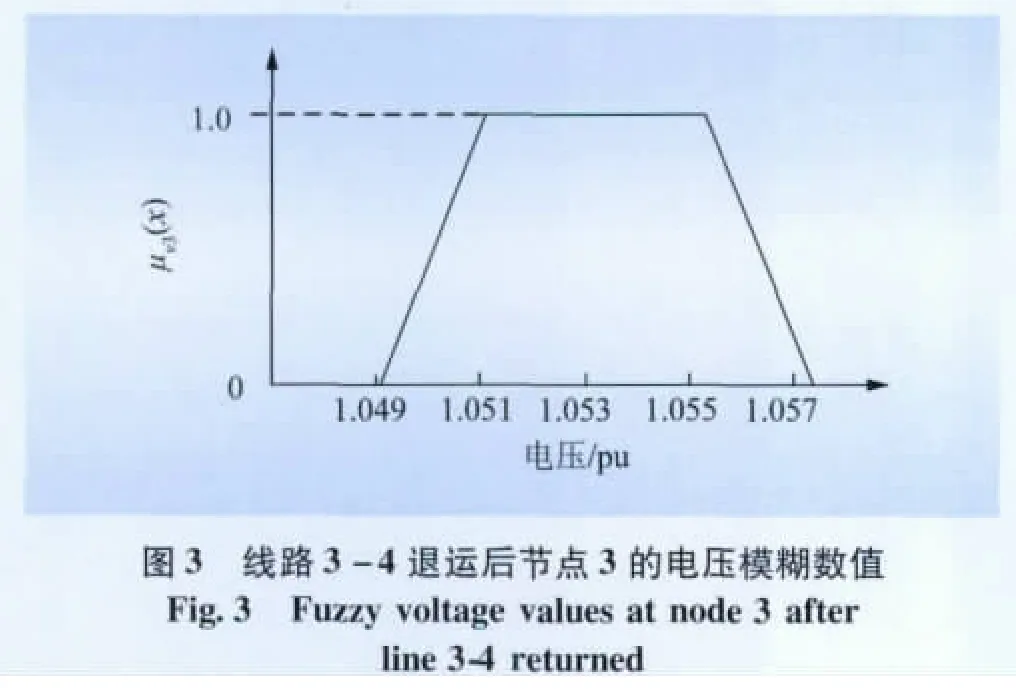
由图3、4结果可看出:

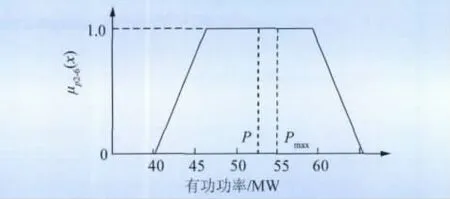
图4 线路3－4退运后线路2－6的有功功率模糊数值Fig.4 Fuzzy active power of line 2-6 after line 3-4 returned

当不考虑不确定性因素的影响时，对线路退运后进行分析得到的是电压和功率的确定值;而在计及不确定性的基础上，对单一线路退运之后进行模糊潮流计算，得到的是潮流(电压、功率)的可能性分布，从而可以得到更为详细的信息，如一些在不考虑不确定性因素影响时某一线路退运后并不会出现过负荷的线路或者不会出现低电压的节点，而在计及不确定性时会有出现过负荷或者低电压的可能。如图4所示，当不考虑不确定性因素时，线路3－4退运后支路2－6的潮流功率为53.05 MW(如图中P所示)，此时支路2－6有功功率小于线路最大传输功率55.09 MW(如图4中Pmax点处，假定最大传输功率为正常潮流功率的1.4倍)，而当考虑不确定性因素后，由支路2－6的潮流分布可能性可以看出，支路2－6有可能发生过载，且是发生在较大的隶属度μ(x)=1下。

此外，从梯形图中还可看出线路发生过载的严重程度，例如当线路功率对应59 MW时，线路发生过载是处在较大的隶属度下μ(x)=1下，且此时线路超过最大功率约4 MW，而这些是通过确定性潮流计算看不出来的。通过对各线路及节点变量的可能性分布进行分析，可为各线路单独退运之后带给系统的危害程度进行比较提供依据。

5 结论

本文研究了计及不确定性的线路退运后的模糊潮流计算方法，采用梯形模糊数处理负荷、发电机出力以及发电机可用度的不确定性，进行一次潮流计算便可得到单一线路开断后潮流分布的可能性程度，同时可得出潮流功率过载以及节点电压出现低电压的可能性大小和严重程度，进一步结合风险评估的方法，便可为线路重要性大小排序提供依据。同样计及不确定性，若仍沿用确定性潮流计算方法，对每一种情况都进行断线分析，则可能需要进行上百次、上千次潮流计算，计算量过大。

［1］王守相，赵玮，王成山，等.计及不确定性的预想事故自动选择区间方法［J］.电力系统自动化，2007，31(20):27-31.

［2］武志峰.计及不确定性的电力系统静态安全分析［D］.天津大学，2007.

［3］董雷，程卫东，杨以涵，等.考虑支路随机断线的概率潮流方法及应用［J］.电力系统保护与控制，2010，38(20):79-84.

［4］Miranda V，Saraiva J T.Fuzzy modelling of power system optimal load flow［J］.IEEE Trans on Power Systems，1992，7(2):843-849.

［5］Saraiva J T，Miranda V，Matos M A.Generation and load uncertainties incorporated in load flow studies［C］.6th Mediterranean Electrotechnical Conference Proceedings，V01.2:1339-1342.

［6］Kaufmann A，Gupta M M.Fuzzy mathematical models in engineering and management science［M］.North Holland ed，1988:32-40.

［7］张焰，陈章潮.电网规划中的模糊潮流计算［J］.电力系统自动化，1998，22(3):20-22.

［8］张焰，陈章潮.计及不确定性的模糊交流潮流计算方法研究［J］.电网技术，1998，22(2):20-22，25.

［9］张焰，谈伟.模糊潮流计算方法研究［J］.电工电能新技术，1999，18(3):9-12.

［10］王锡凡.现代电力系统分析［M］.北京:科学出版社，2003.

［11］王锡凡，王秀丽.实用电力系统静态安全分析［J］.西安交通大学学报，1998，22(1):25-36.

［12］张伟，卫志农，刘玉娟.基于混沌优化的含风电场的最优潮流计算［J］.中国电力，2011，44(10):25-28.