1 000 kV构架风振系数的计算研究

朱海维，马勇杰，吴伟康

(华东电力设计院，上海市200063)

0 引言

在1 000 kV晋东南—南阳—荆门特高压输变电试验示范工程中，众科研设计单位对1 000 kV构架的结构体系及选型、根开、荷载、节点等进行了大量的分析及研究，并出版了相应的专题报告及设计导则。经比较发现，这些分析与研究多偏向于工程的安全性及经济性，并未对1 000 kV构架的风振响应进行分析。

1 000 kV南阳站扩建工程需在串补配电装置区域新建数榀单排单跨1 000 kV构架，结构形式与联合式布置有较大差别，根开、断面、杆件布置及规格、质量等方面均进行了优化。其中1榀1 000 kV构架高90 m，导线挂点高55 m，根开3.5 m×9 m，自振周期大，在风激励下的动力响应比较显著，其在风荷载作用下的安全性有待理论分析进一步验证。

本文针对该1 000 kV构架，对其动力特性、风振响应、风振系数等进行分析及研究，以期得出一些有益的结论，用于指导后续1 000 kV构架的设计。

1 1 000 kV构架的动力特性

1 000 kV构架的工程实景和结构布置如图1所示。

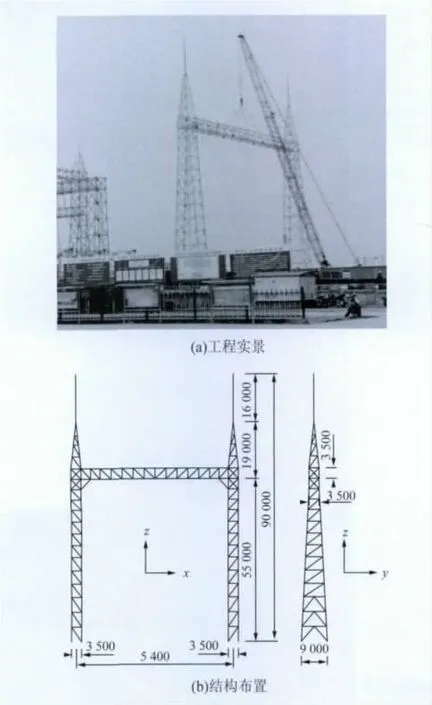
图1 1 000 kV构架工程实景和结构布置Fig.1 Project picture and structural layout of 1 000 kV structural gantry

采用Ansys有限元软件分析1 000 kV构架的动力特性时，首先需要根据构架的受力特性，合理地选取梁、杆单元。通常情况下，1 000 kV构架采用整体空间桁架模型进行设计计算，即以整个构架为超静定空间体系，节点作为理想铰来考虑，所有杆件只受轴力作用。而在实际工程中，构架的节点连接及构造与简化模型并不完全一致，如构架柱、梁主材采用法兰连接，受力性能偏向于梁，其他斜杆多采用单插板或U插板连接，受力性能则偏向于杆。因此，采用Ansys软件分析时，柱、梁主材采用Beam4单元，其余杆件采用Link8单元。

由于节点及单元数量较少，为了获得较高的计算精度，采用子空间迭代法计算1 000 kV构架的振型，其在x向与y向的前2阶振型及一阶扭转振型如图2所示。

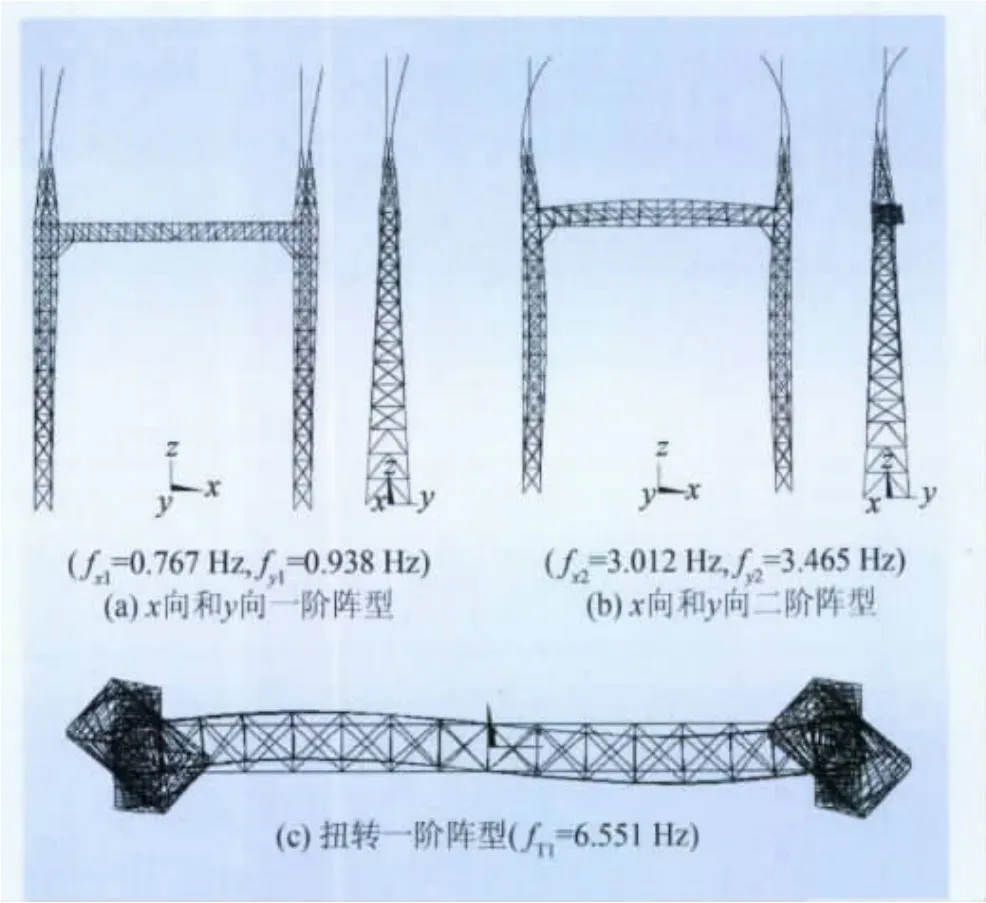
图2 x向、y向及扭转阵型Fig.2 Vibration mode in x and y directions and torsion

从振型及频率的计算结果可以看出，构架x向与y向的一阶振型频率相当，x向较y向低18%，二阶振型频率是一阶的3倍以上，扭转振型频率亦远高于x向与y向一、二阶振型频率，这说明构架为可忽略扭转影响的高耸结构，结构体系合理，进行设计计算时，可仅考虑一阶振型的影响。

2 脉动风荷载的模拟

自然风的模拟必须使模拟风与自然风的基本特性，如平均值、与高度有关的自功率谱和互功率谱以及相位角关系等尽可能接近［1］。目前，模拟脉动风速的方法主要有3种:线性滤波法、谐波叠加法及小波法。其中线性滤波法是将随机过程抽象为满足一定条件的白噪声，然后根据一定的方法变换拟合出该过程的时域模型，其中的自回归(auto-regressive，AR)模型因其计算量少、速度快而广泛用于随机振动的时间序列分析中。

本文采用AR法对随机风谱进行模拟，M个点空间相关脉动时程 V(X，Y，Z，t)列向量的 AR模型［2］为

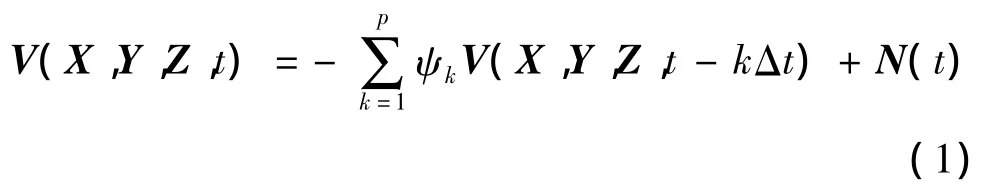
式中:X =［x1，x2，…，xM］T;Y =［y1，y2，…，yM］T;Z=［z1，z2，…，zM］T;(xi，yi，zi)为空间第 i点坐标，i=1，…，M;p为AR模型的阶数;Δt为模拟风速时程的时间步长;ψk为M×M阶AR模型的自回归系数矩阵;N(t)为独立过程随机向量。

风速谱采用Davenport谱，为

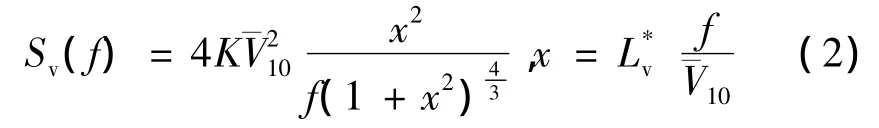
自相关函数采用Shiotami建议的相关函数，为

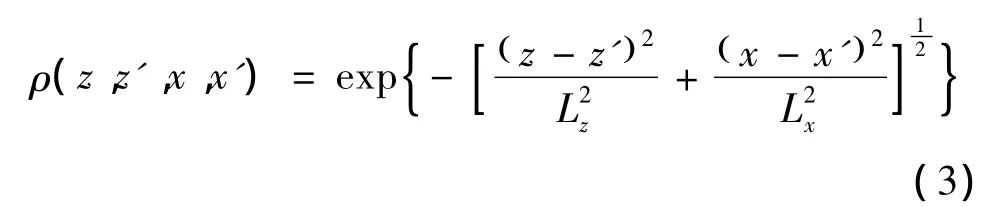
采用AR法模拟风荷载时，模拟基本参数见表1。对于1 000 kV构架，根据分段，构架可简化为如图3所示的平面质点模型，仅考虑其在x向及z向的相关性。构架顶部(74 m)的模拟结果如图4～6所示。

表1 脉动风速模拟参数Tab.1 Simulation parameters of fluctuating wind velocity

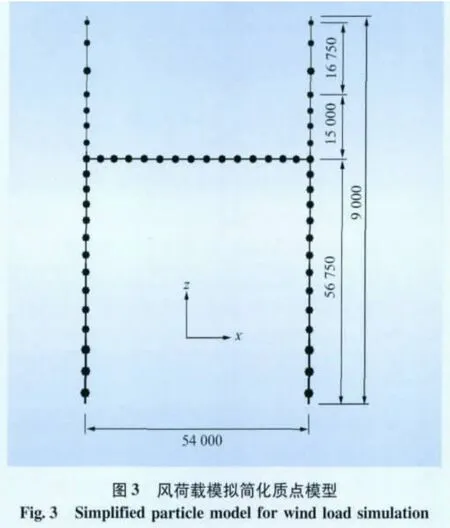
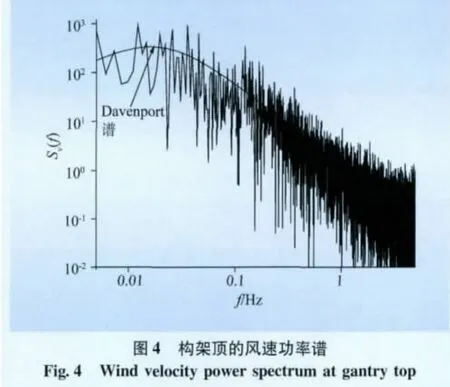
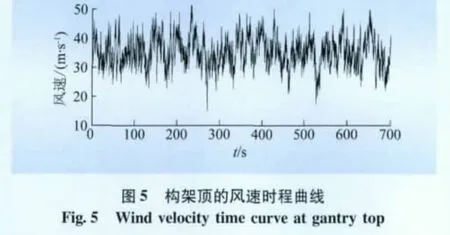
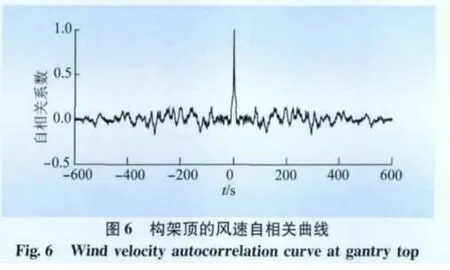
从图4～6中可以看出，模拟的风速谱与Davenport谱吻合良好，平均风速与理论值一致，脉动风速为0均值高斯过程，自相关系数曲线与假设吻合良好。因此，可以认为模拟所得到的脉动风速谱能够在一定情况下模拟真实风场，可以用于后期的风振响应时程分析。

3 1 000 kV构架风振响应分析

采用AR自回归模型模拟得到的结果仅为各简化质点脉动风速，需要转换为节点荷载并施加到Ansys有限元模型中。根据DL/T 5154—2002《架空送电线路杆塔结构设计规定》［3］，结合本文风谱模拟特点，杆塔各分段的平均风荷载、脉动风荷载按式(4)计算。

式中:w为平均风压或脉动风压;Af为杆件承受风压投影面积;μs为构架体型系数。

根据整体空间桁架法的计算原则，再将每段计算所得的平均风荷载及脉动风荷载平均分配到该段的各节点上。结构在风荷载作用下的动力方程为

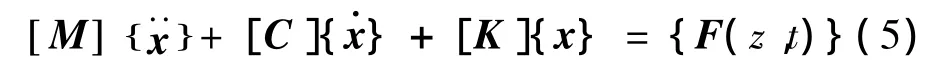
式中:[M]、[C]、[K]为结构的质量、阻尼、刚度矩阵;为结构顺风向位移、速度、加速度向量;{F(z，t)}为脉动风荷载向量。

阻尼是影响结构风振响应的重要因素［4-5］，其大小不仅与使用的材料、结构的连接方式和施工过程有关，而且与结构的振动频率、外激励频率以及振幅呈非线性关系。本文在进行构架风振响应的分析时，采用Rayleigh阻尼，得

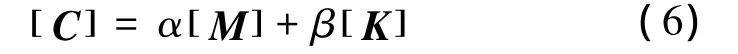
式中:α、β分别为质量比例阻尼和刚度比例阻尼。如已知2个特定振型的圆频率ωm、ωn及相关的阻尼比ζm、ζn，可按式(7)计算。

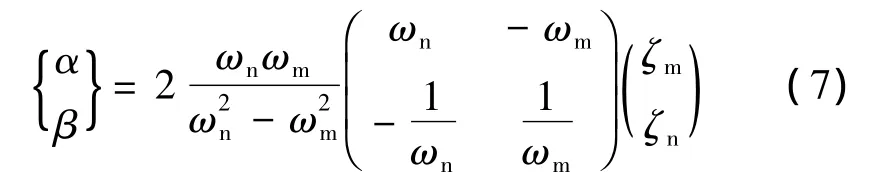
对于本文所分析的1 000 kV构架，如荷载作用于x向时，取x向固有的前两阶振型频率;荷载作用于y向时，取y向固有的前两阶振型频率;阻尼比的取值，参考文献［6］，取为0.02。则式(7)可简化为

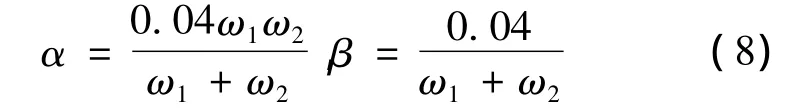
根据Ansys软件分析所得的振型频率，由式(8)计算可得1 000 kV构架的比例阻尼α、β，见表2。

表2 Rayleigh比例阻尼取值Tab.2 Rayleigh proportional damping value

需要指出，由于平均风的周期较大，能产生相当于静力作用的效应，而脉动风的周期较小，且为随机，为了避免将大周期的平均风作为突加动力荷载作用进行计算，采用Ansys软件进行瞬态分析时，需要先将平均风荷载作为等效静力荷载进行计算，再根据其计算结果进行下一步脉动风荷载的计算，同时考虑脉动风荷载所产生的动力效应。

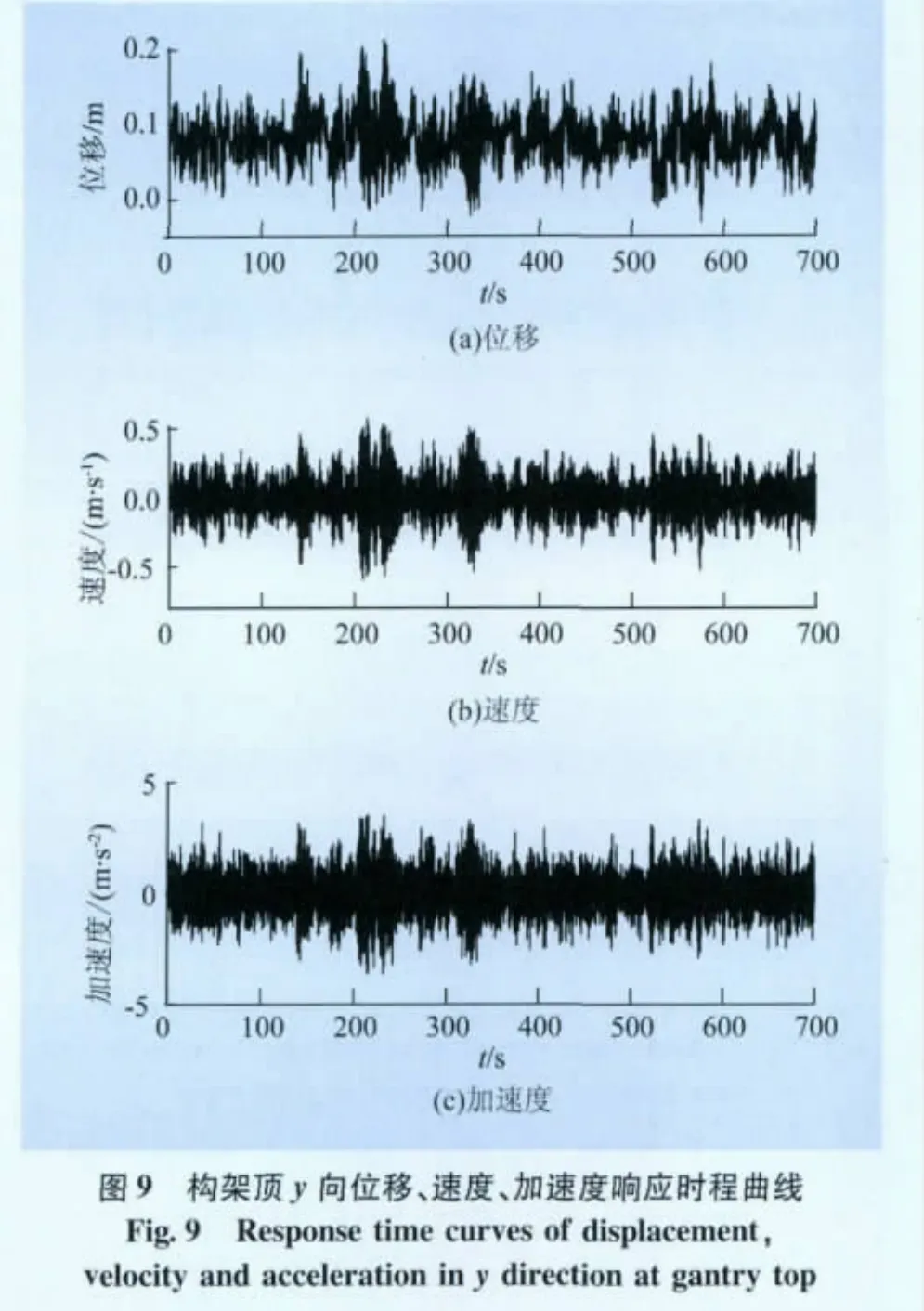
本文分别对1 000 kV构架在x向及y向风荷载作用下的风振响应进行时程分析。以构架顶部(74 m)节点为例，其x向及y向的位移、速度、加速度时程曲线以及由快速傅里叶变换得到的位移、速度、加速度功率谱曲线分别如图7～10所示。

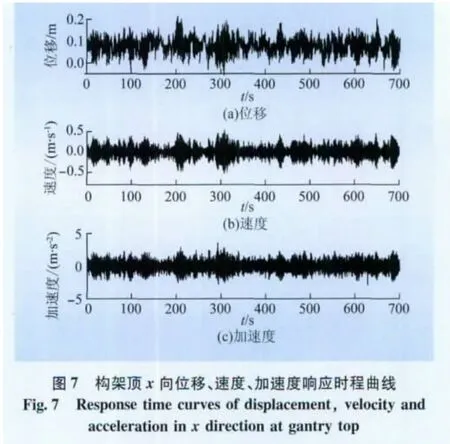
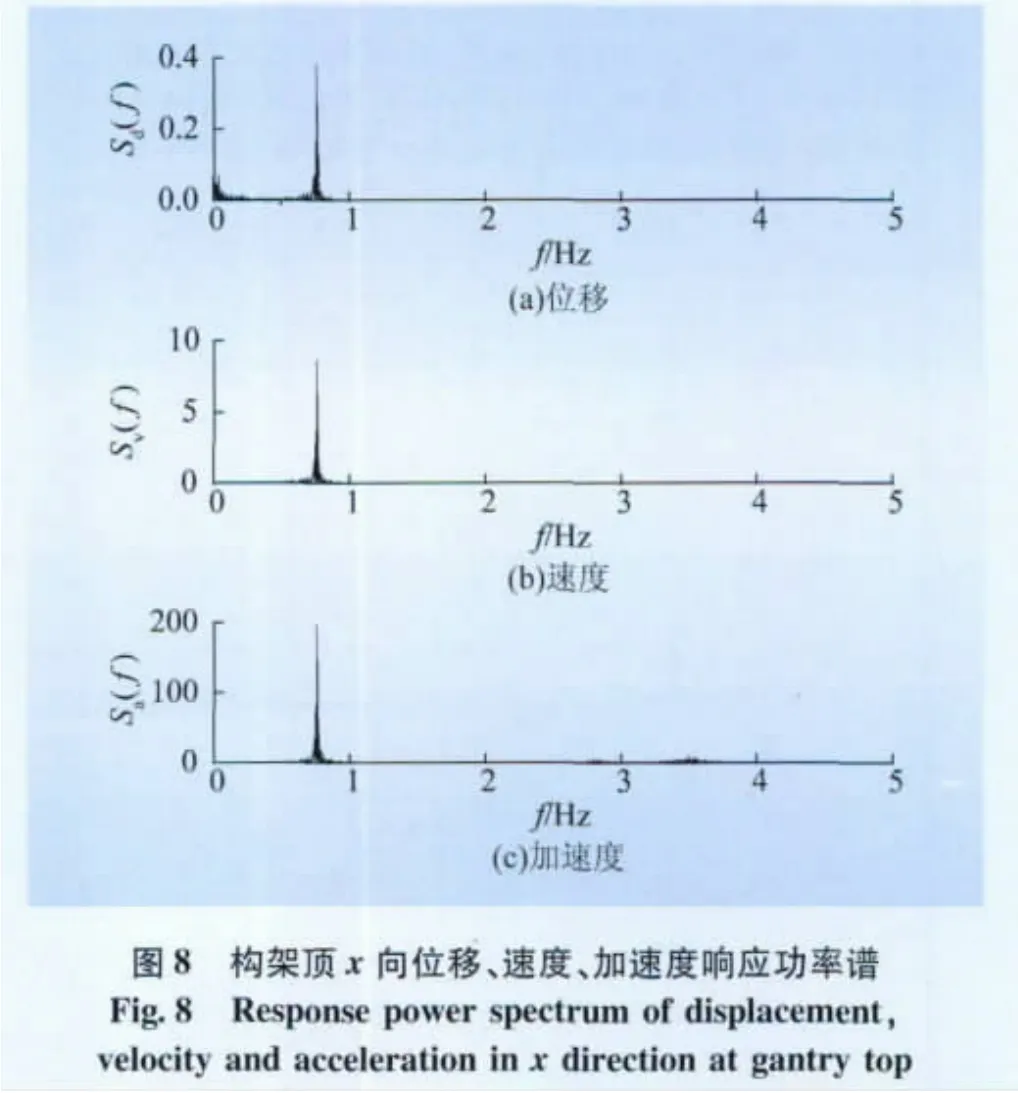
从时程曲线可以看出，构架顶点处的速度和加速度均值为0，位移均值为静力加载位移，表明模型荷载施加方法与设计一致。从功率谱曲线来看，构架顶部(74 m)x向风振响应频率集中在0.75～0.77 Hz之间，与x向一阶振型频率一致;y向风振响应频率集中在0.92～0.94 Hz之间，与y向一阶振型频率一致;这说明构架顶部的风振响应以一阶振型为主，符合一般高耸结构规律。

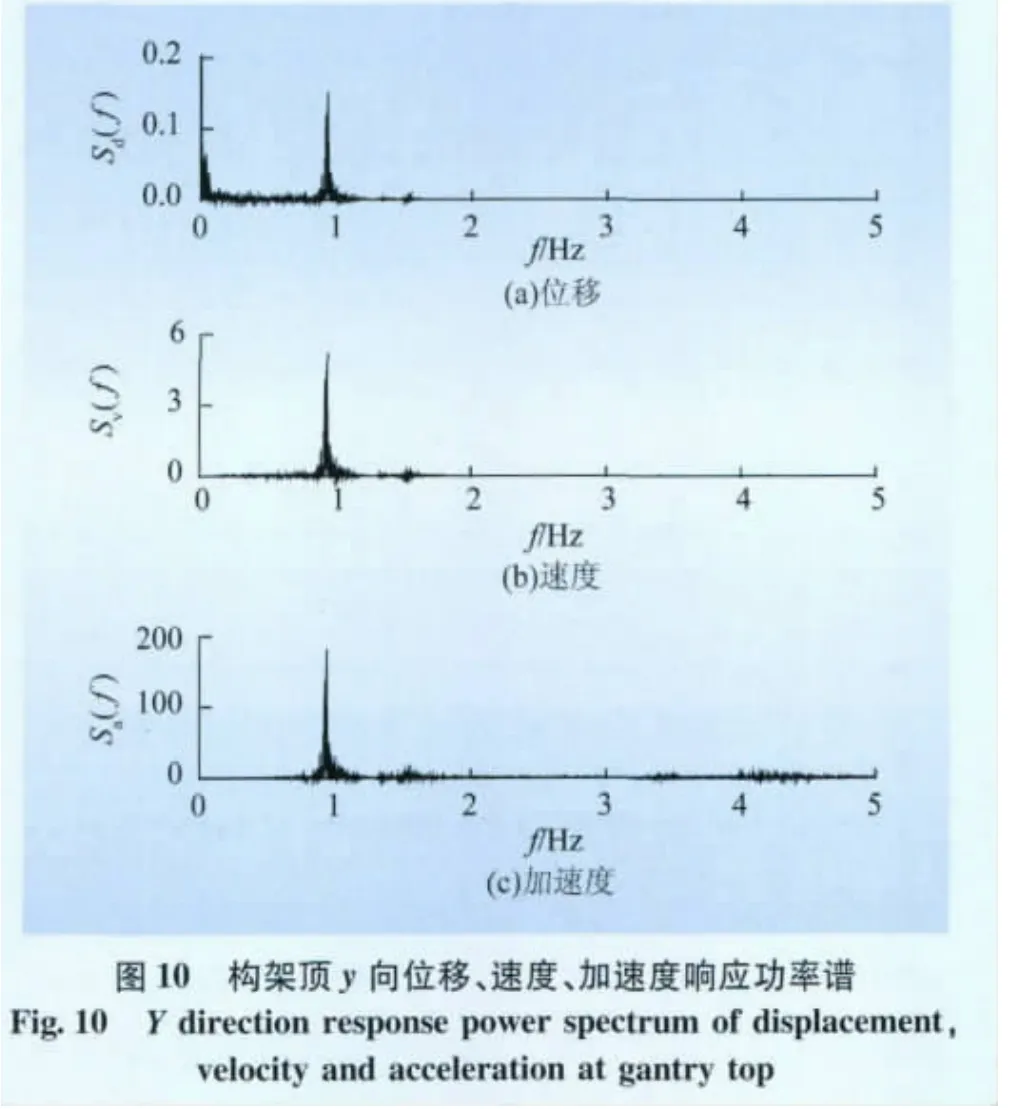
为了分析构架沿高度方向风振响应频率的变化，取构架顶部(74 m)、横梁(55 m)、柱中部(28.5 m)、柱脚(5 m)节点x向及y向的风振响应功率谱进行比较，由于加速度功率谱直接代表了结构的动力响应，频率特征更显著，因此本文仅对加速度功率谱进行比较，如图11～12所示。

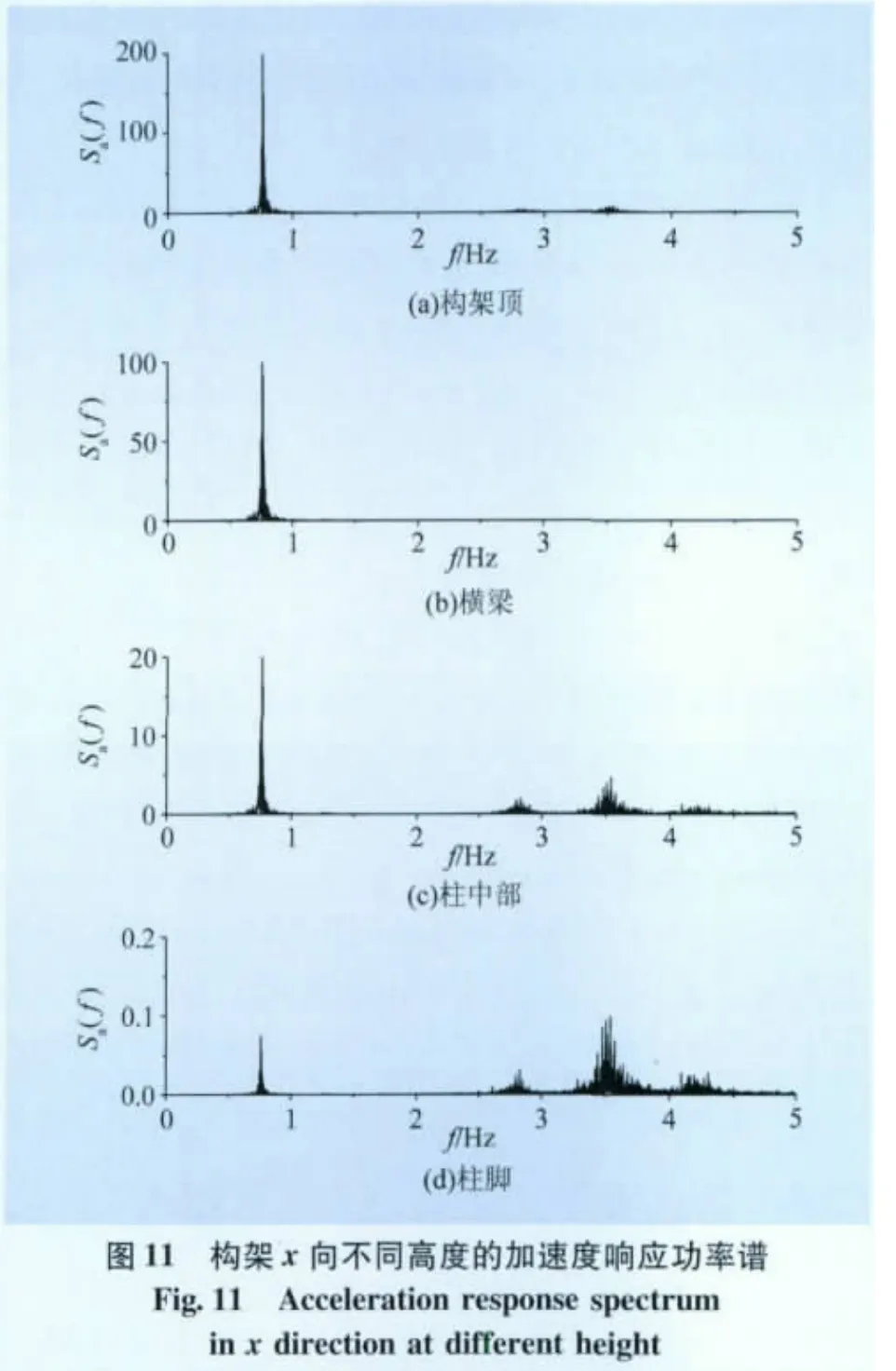
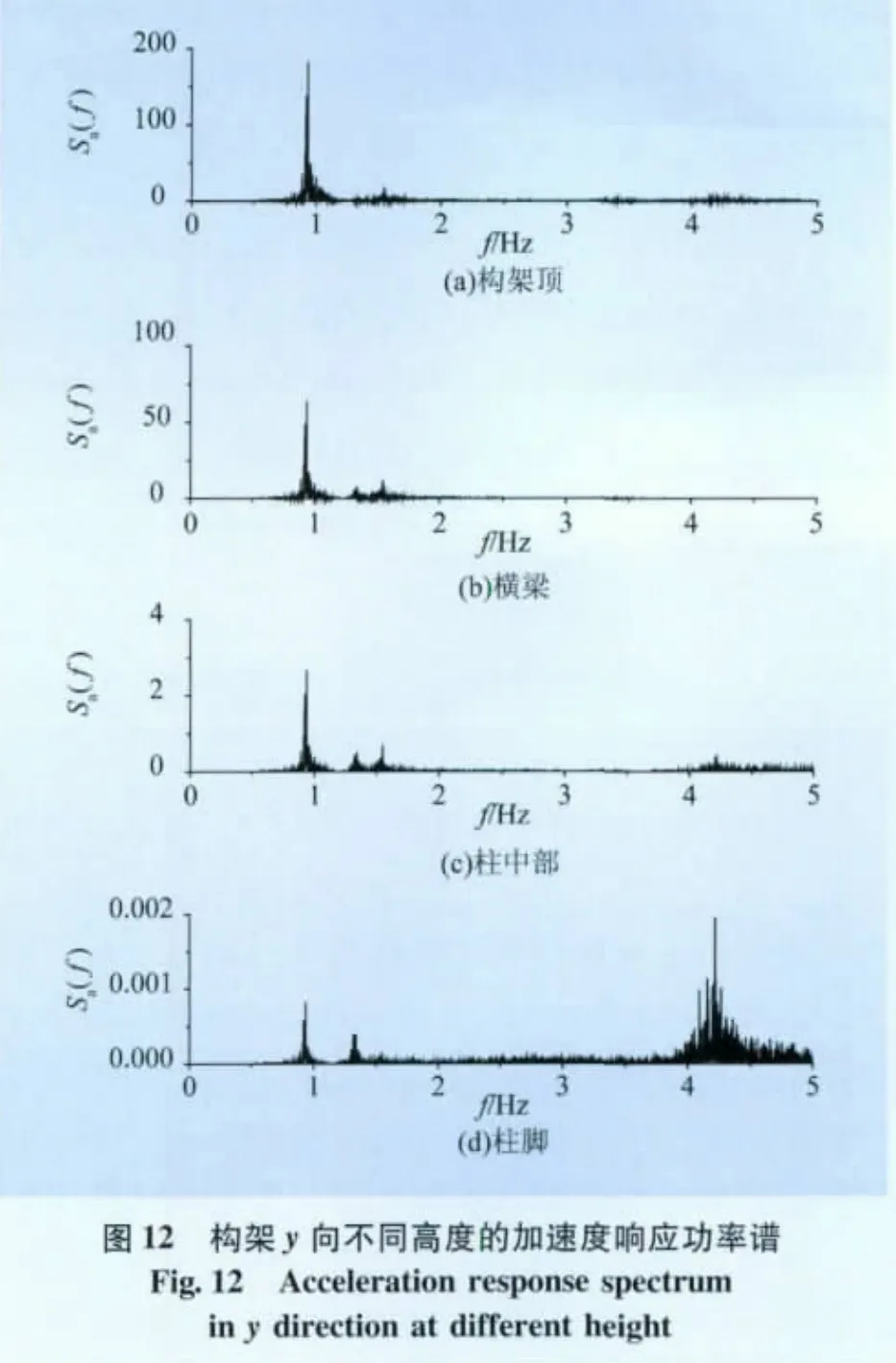
从功率谱曲线来看，不论是在x向还是y向，构架顶部均以一阶频率响应为主;在构架柱的中部，二阶频率响应开始变得显著;在柱腿，响应大部分集中在二阶频率附近。因此可以认为，构架顶部响应以一阶振型为主，中部响应以一、二阶振型为主，底部以二阶振型为主。从频率响应所对应的功率值来看，构架中部及底部二阶频率响应的功率值都相对较小，因此，在构架设计时可以只考虑一阶振型的影响。

4 1 000 kV构架风振系数的计算

在水平风的作用下，结构将在各个方向产生振动，由于脉动风的变化快、周期短、具有随机性，将引起结构的随机振动。当结构的抗风验算方向与风向一致时，结构发生顺风向风振响应。现行设计多为静力设计计算，以风振系数来考虑脉动风对结构的动力影响。文献［7］认为，风振计算应按随机振动理论进行，应考虑多个振型的影响，而且结构的自振周期(包括振型)应按结构动力学计算。对只考虑第1振型影响而可用风振系数来分析比较方便的结构，只限于不考虑扭转影响的高层建筑、高耸结构以及第1振型影响明显起主要作用的结构。

本文1 000 kV构架的一阶自振周期约为1.3 s，风振响应显著。根据上述分析可以认为，本文设计的1 000 kV构架为可只考虑第1振型影响而可用风振系数来分析的高耸结构。

在我国现行规范中，文献［8］未针对1 000 kV构架的风振系数取值进行说明;文献［3］对杆塔高度不超过60 m时，提供了一个沿杆塔全高统一的风振系数，计算及使用均较为方便，但是该方法仅适用于高度小于60 m的杆塔;文献［7］中的风振系数计算公式复杂，并且不完全适用于1 000 kV构架。

根据随机振动理论来推导风振系数的计算方法十分复杂，在已经对脉动风荷载进行模拟、对结构的风振响应进行分析的基础上，可以直接根据风振系数的定义，按式(9)计算构架的风振系数。

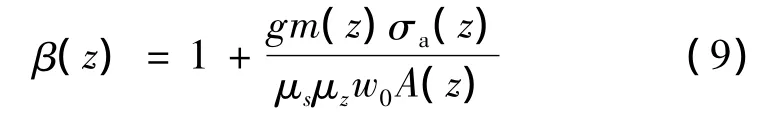
式中:m(z)、σa(z)、A(z)分别为 z高度处的集中质量、加速度方差以及挡风面积;g为保证系数，根据参考文献［9］取为2.2。

本文设计的1 000 kV构架为对称结构，根据其对称性，在计算构架的风振系数时，将构架等效为一根带有N个质点的悬臂杆，其中，横梁一半的质量施加在与柱高度相同的质点上。简化后，构架沿高度方向各个质点的加速度响应方差如图13所示，根据式(9)计算得到的各分段风振系数如图14所示。

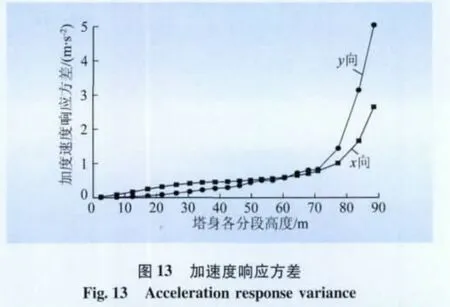
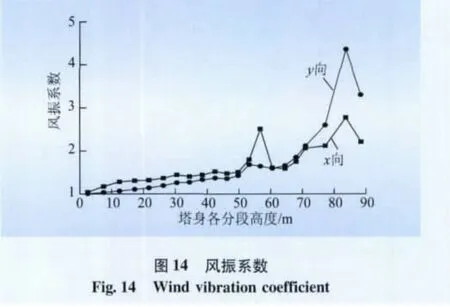
从图13、14可以看出，1 000 kV构架x向及y向的风振响应并不完全相同，通过理论计算得到的风振系数并不与高度完全成正比，x向风振系数在构架横梁处存在较大的突变。

(1)在横梁以下，构架柱y向根开大于x向，y向刚度大于x向，因此，横梁以下y向的加速度响应方差、风振系数均较x向小。

(2)在横梁以上，构架x向与y向刚度相同，但由于构架整体在x向的刚度较弱，顶部的协同效应导致其x向加速度响应方差、风振系数反而较y向小。

(3)在构架横梁处，横梁的质量全部集中在构架柱上，对于y向存在与其质量相当的风荷载作用，该段风振系数与下段相比并未产生明显变化，而在x向，横梁质量不变，但风荷载减小，使得构架x向风振系数在横梁处存在较大的突变。

(4)避雷针部分为悬臂结构，风振响应极为明显，因此，风振系数较格构式部分有较大的增加，仅在针尖部分因其质量小，受风面积相对较大，风振系数急剧减小。

5 杆件内力比较

在设计1 000 kV构架时，为了计算方便，参考杆塔规范，根据工程经验，除避雷针部分风振系数按悬臂构件风振系数取2.0外，格构式部分参考文献［3］，结合工程设计经验，即塔高超过60 m时，每增高5 m则风振系数增加0.05，1 000 kV构架沿全高取统一风振系数1.7进行计算。而理论计算表明，构架顶部避雷针部分的风振系数为2.5～4.4;格构式部分风振系数沿高度的加权平均值，x向为1.67，y向为1.54。

根据理论计算所得各分段风振系数，构架在x向及y向风荷载作用下各分段杆件最大内力与设计取值的比较如图15所示。

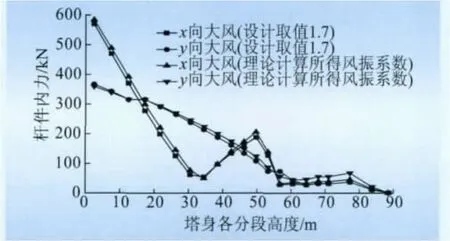
图15 采用不同风振系数计算所得杆件内力Fig.15 Characteristic value of member forces calculated by using different wind vibration coefficients

从图15中可以看出，不论是在x向还是y向风荷载作用下，除柱顶部分外，1 000 kV构架采用2种风振系数计算所得杆件内力相差均不大，考虑到构架还受导地线、结构自重等荷载作用，风荷载作用仅占40%左右。工程设计时，在取值合理的情况下，1 000 kV构架格构式部分可参考文献［3］沿全高取统一风振系数计算;构架高度超过60 m时，每增高5 m风振系数增加0.05，顶部悬臂避雷针宜按“2.0+下部格构式部分风振系数”进行取值。除柱顶部分外，柱横梁以下部分在x向风荷载作用下杆件内力的大小及变化趋势均与y向存在较大差别，因此在设计构架时，应至少考虑这2个方向风荷载的作用。

6 结论

(1)1 000 kV构架为可忽略扭转影响的高耸结构。

(2)1 000 kV构架顶部响应以一阶振型为主，中部响应以一、二阶振型为主，底部以二阶振型为主。由于一阶与二阶频率相差较大，一般情况下设计时可仅取一阶振型。

(3)1 000 kV构架x向及y向的风振响应并不完全相同，采用数值模拟，通过理论计算所得的风振系数并不与高度完全成正比，x向风振系数在构架横梁处存在较大的突变。

(4)1 000 kV构架设计时，格构式部分在高度未超过规范限值较多的情况下可参考文献［3］沿全高取统一风振系数计算，构架高度超过60 m时，每增高5 m风振系数增加0.05，顶部悬臂避雷针宜按“2.0+下部格构式部分风振系数”进行取值。实际计算表明，只要取值合理，与根据各分段实际风振系数计算所得杆件内力的误差较小。

(5)构架设计时，应至少考虑x向及y向2个方向风荷载的作用。

(6)对于复杂结构风振系数的取值，在缺乏规范参考的情况下，可以通过程序来模拟风速谱，利用Ansys有限元软件进行风振响应时程分析，并结合理论公式计算结构各分段的风振系数。

［1］王肇民，马人乐等.塔式结构［M］.北京:科学出版社，2004.

［2］舒新玲，周贷.风速时程AR模型及其快速实现［J］.空间结构，2003，9(4):27-32.

［3］DL/T 5154—2002架空送电线路杆塔结构设计技术规程［S］.中国电力出版社，2002.

［4］H.Yasui，H.marukawa etc.Analytical study on wind-induced vibration ofpowertransmission towers［J］.JournalofWind Engineering and Industrial Aerodynamics，1999，83:431-441.

［5］R.克拉夫，J.彭津.结构动力学［M］.北京:高等教育出版社，2006.

［6］张相庭，王志培等.结构振动力学［M］.上海:同济大学出版社，2005.

［7］GB 50009—2001建筑结构荷载规范(2006年版)［S］.中国建筑工业出版社，2002.

［8］NDGJ 96—92变电所建筑结构设计技术规定［S］.能源部电力规划设计管理局，1992.

［9］张相庭.结构风工程理论·规范·实践［M］.北京:中国建筑工业出版社，2006.

［10］克莱斯·迪尔比耶，斯文·奥勒·汉森著.薛素铎等译.结构风荷载作用［M］.北京:中国建筑工业出版社，2006.

［11］邓洪洲，张永飞，等.输电塔风振响应研究［J］.特种结构，2008，25(2):9-13.

［12］ASCE 74—2009.GuidelinesforElectricalTransmission Line Structural Loading［S］.American Society of Civil Engineers，1991.

［13］ANSI/ASCE 10—90.Design ofLatticed SteelTransmission Structures［S］.Published by theAmerican Society ofCivil Engineers，New York，1991.

［14］朱海维.输电线路塔线耦合体系风振响应分析［D］.上海:同济大学，2008