用于电网削峰填谷的储能系统容量配置及经济性评估

修晓青，李建林，惠东

(中国电力科学研究院，北京市100192)

0 引言

近年来，随着人民生活水平的提高和电力负荷的快速增长，电网负荷峰谷差逐步增大，与此同时，随机性、波动性、不可调度性的可再生能源大规模并网，导致电网的调峰问题更加突出，也给电力调度造成一系列的困难。电力系统中电源及输配电设备均按照电网高峰负荷规划建设，但电网高峰负荷持续时间较短，导致为满足高峰负荷需求而规划建设的电力设备资产利用率较低。研究解决电网调峰问题、提高资产利用率是现阶段电网建设面临的一个重要课题。

我国的电源结构以火电为主，大多数常规火电机组能够灵活调节出力的能力不足额定容量的50%，当负荷峰谷差低于火电机组的调整范围时，需要部分小容量机组启停调峰或压火调峰，甚至需投资建设更多的机组并改进火电机组的运行方式来满足调峰需求，从而大幅增加了系统的运行成本［1-3］。据统计，近年来我国电网负荷的峰谷差为38% ～48%［4］。以辽宁电网为例，2011年辽宁电网峰值负荷为22 362 MW，低谷负荷为12 708 MW，峰谷差为43.2%。

调峰问题是电网运行中的基本问题。启停迅速、运行方式灵活的调峰技术符合电网调峰技术的应用需求。在电力系统常规调峰技术中，相比于火电机组，水电机组启停迅速、运行方式灵活，且调峰深度接近100%［4-5］，但水电机组的建设受地理条件的限制，不能进行大规模的推广应用。

大规模电池储能系统因其快速响应特性，具有优越的调峰性能，可在用电低谷期作为负荷存储电能，在用电高峰期作为电源释放电能，实现发电和用电间解耦及负荷调节，削减负荷峰谷差，且其建设不受地理条件限制。以锂离子电池、全钒氧化还原液流电池、钠硫电池为代表的电池储能系统，可有效延缓甚至减少电源和电网建设，提高能源利用效率和电网整体资产利用水平，改变现有电力系统的建设模式［6-7］。

影响储能技术在电力领域规模化应用的主要因素主要包括储能系统规模、技术水平、安全性及经济性。当储能系统的容量达到MW/MWh级规模能力、满足MW/MWh级下的安全性、循环寿命达到5 000次及以上、充放电效率达到80%及以上时，储能系统的高成本成为限制其大规模应用的关键因素，从而有必要研究储能应用的容量配置问题，进而评估储能项目运营的经济性。储能系统的应用研究主要包括2个层次:(1)在规划前期，根据储能系统应用方向，配置储能系统容量，并进行经济性评估;(2)在储能系统运行过程中，根据储能系统应用目标，研究储能系统在线优化控制问题，文献［8-9］对电池储能系统削峰填谷的在线优化控制进行了研究，文献［10-15］研究了风电场中储能容量的配置方法。关于规划前期，储能系统参与调峰的容量配置及经济性问题对储能产业的发展意义重大，本文将重点围绕此问题展开研究。

1 储能系统容量配置策略

储能系统接入电网示意图如图1所示，储能电池经直交变换、升压变压器升压后接入大电网。

储能技术用于电网削峰填谷的容量配置，包括功率配置和容量配置。储能系统的功率需满足系统调峰的功率限值，功率和容量的计算公式为

图1 储能系统接入电网示意Fig.1 Energy storage systems integrated to grid

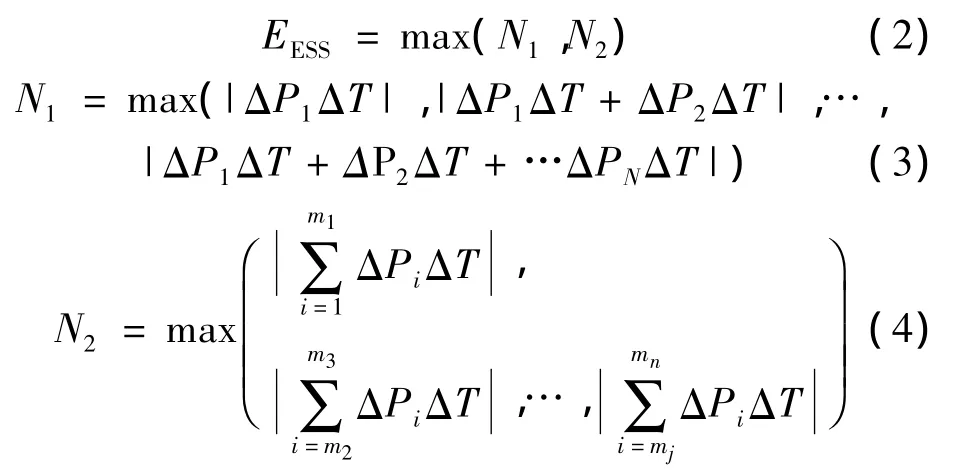
式中:PESS为储能系统功率;EESS为储能系统容量;ΔPi为各个时刻储能系统出力需求;ΔT为样本数据采样时间间隔;1～m1、m2～m3，mj～mn为样本数据中需要储能不间断充电 /放电的数据采样时刻，其中不间断充电时间定义为连续不放电时间，不间断放电时间定义为连续不充电时间。

考虑储能系统充放电平衡约束，控制储能系统的充放电，控制策略如下:

(1)导入待处理的负荷数据，统计负荷的峰值与谷值;

(2)根据负荷峰谷值，设定储能调节后合成出力低谷值Pref，并为合成出力峰值赋初值Pmax;

(3)系统循环赋初值n=1;

(4)比较负荷与Pref、Pmax的大小关系。当负荷小于Pref时，储能电池充电;当负荷大于Pmax时，储能电池放电;负荷在Pref、Pmax之间时，储能电池不动作。

(5)n=n+1;

(6)若n小于所载入负荷数据的条数时，返回步骤(4)，否则进行步骤(7);

(7)统计储能电池的充电电量、放电电量;

(8)判断储能电池充放电是否平衡。若充电电量大于放电电量，减小Pmax，返回步骤(3);若充电电量小于放电电量，增大Pmax，返回步骤(3);若充放电平衡，由式(1)～(4)计算储能系统的功率、容量。

2 经济性分析

2.1 成本分析

电池储能系统成本主要包括初始投资成本和运营维护成本。储能系统的初始投资成本主要由功率成本和容量成本构成。容量成本与储能电池的投资有关，功率成本与储能电池用双向变流器、监控系统的投资有关。储能系统的运行维护成本为维持储能电站处于良好的待机状态所需要的费用。

储能系统循环寿命是其成本分析中的重要参量。储能系统的循环寿命，即标称容量降至储能电池初始额定容量的80%时，电池的完整充放电循环次数。影响电池循环寿命的主要因素包括极端温度、过度充放电、充放电深度及充放电速率。储能系统在标准充放电电流、电压、温度条件下工作时，其循环寿命为充放电深度的函数。储能系统使用寿命年限为

式中:Tlife为对应充放电深度下储能系统的循环寿命;Lcyc_year为年充放电循环次数。

假定不考虑储能系统正常使用期内的设备更换成本，为便于分析，根据储能系统的使用寿命和基准收益率，可将储能系统的总投资成本在寿命期内进行成本分摊，与储能系统的年维护成本叠加，得到储能系统的费用年值。储能系统费用年值为

式中:Cp为储能系统单位功率成本;CE为储能系统单位容量成本;PESS为储能系统额定功率;EESS为储能系统额定容量;n为储能系统使用寿命年限;i为储能项目投资收益率;Cm为储能系统单位运维成本;Q为储能系统年发电量。

2.2 经济效益分析

储能系统定位为电网负荷削峰填谷，其经济效益包括直接效益和间接效益。直接效益主要来自于储能系统采取削峰填谷模式运营，通过电网用电高峰与用电低谷的电价差获取的经济效益。储能系统的间接效益主要包括节煤效益、环境效益以及储能系统延缓发输配电设备投资带来的经济效益。

储能系统的经济效益Iincome可分为功率效益、容量效益和环境效益，计算式为

式中:Rp_vest为常规发电机组单位功率投资额;Rout为储能系统上网电价;Rin为储能系统充电电价;RTP为常规火电机组的单位供电成本;Vi为储能减少第i种污染物排放带来的环境效益;n为污染物总数;Qi为第i种污染物的排放量。

影响储能系统投资经济性的相关指标主要包括峰谷价差，储能系统功率、容量、投资成本、运行维护成本、充放电深度及相应充放电深度下的循环寿命［16-17］，以及常规火电机组投资额、发电成本、环境成本等。用于评估削峰填谷的储能系统投资经济性的数学模型为

由式(8)可知，仅当S＞0时储能系统的投资具备经济性。储能系统投资具备规模经济性的条件为

3 仿真研究

以某地区2011年11月份的实际负荷数据为例进行分析，该地区凌晨0:00～6:00为用电低谷期，上午11:00前后为用电小高峰，晚17:00前后为用电高峰期。峰值负荷为 22 207 kW，低谷负荷为17 761 kW，峰谷差为20%。

采用锂离子电池储能系统对电网负荷调峰，将用电低谷期负荷抬升至18 761 kW时，可将峰荷期常规机组出力降至20 525 kW，储能系统完成一个完整充放电过程，所需储能系统的功率为1 681 kW，容量为4 100 kW·h，此时峰谷差降为8.6%。负荷与储能的合成出力及负荷曲线如图2所示。

图2 负荷与储能系统合成出力曲线Fig.2 Synthetic output curves of load and energy storage system

参与电网调峰的储能系统容量与储能系统的调峰程度、当地电网负荷特性密切相关。储能系统功率和容量需求如图3所示。本地区的电网负荷，随着调峰程度的增加，所需储能系统的功率、容量随之增加。储能系统的功率受限于峰值负荷的调节量，仿真结果表明，该地区储能系统的功率与峰值负荷功率的减小量相同。

考虑储能系统的循环寿命，仿真过程中设定储能系统的荷电状态范围为［0.1，0.9］，每天完成1个完整充放电循环，并且以天为单位满足充放电平衡约束，使用寿命约为15年。根据储能系统容量配置与电网负荷调节量的关系，从社会整体效益和投资者角度分别分析储能系统的经济效益。

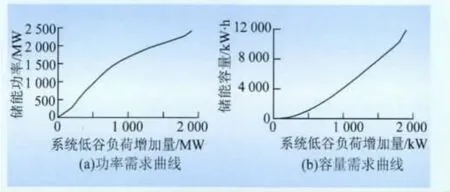
图3 储能系统功率和容量需求曲线Fig.3 Power demand and capacity demand curves of energy storage system

(1)社会整体效益角度。以S为目标函数，分析储能系统不同容量配置下的经济性。在现有技术经济水平下，锂离子储能电池成本约为4 500元/(kW·h)，监控成本为5 000元/kW，常规火电机组的单位投资成本为374.72元/(kW·a)，220 kV输电设备的单位投资成本为594元/(kW·a)，相关参量设置见表1［18-20］。

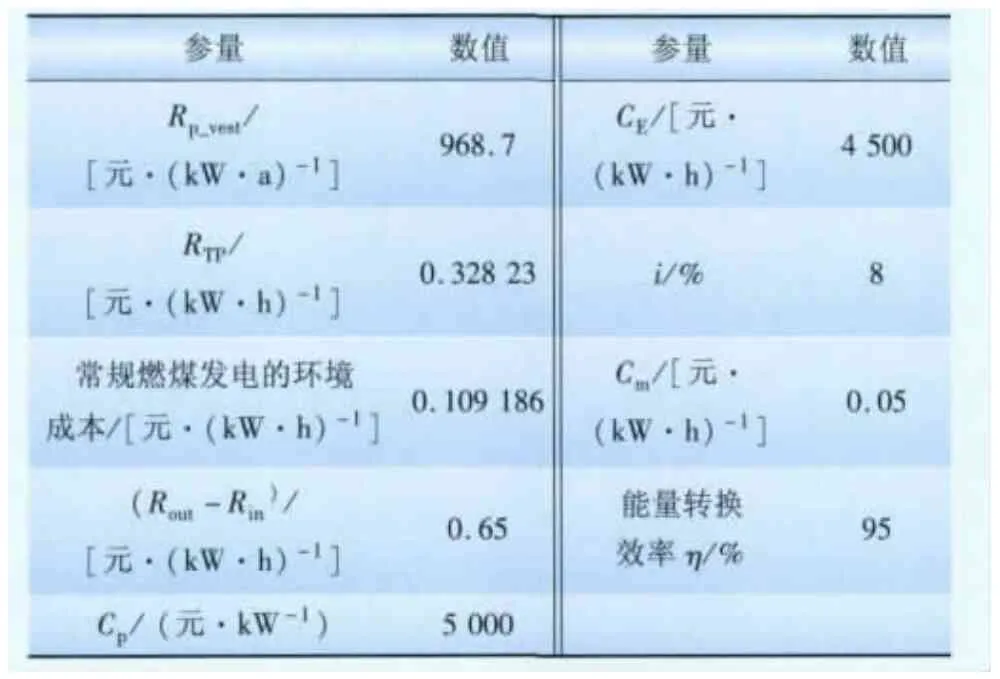
表1 参量设置Tab.1 Parameters setting

电网中配置储能进行削峰填谷的经济效益如图4所示。从图4中可看，随着所配置储能系统功率的增加，储能系统年收益先升高后降低。当储能系统功率为753 kW、容量为684 kW·h时，年收益最大为13 740元，此时的峰谷差为15.3%，峰谷差降低了4.7%。分析储能系统投资经济性数学模型可得，储能系统功率增大时，造成年收益下滑的主要原因是现阶段储能系统成本过高。因此有必要分析储能电池在不同成本下的收益曲线情况。

图4 储能系统削峰填谷经济效益Fig.4 Economic benefits of peak load shifting of energy storage system

储能系统不同成本下的收益如图5所示。根据图5可知，随着每kW·h储能成本C［单位为元/(kW·h)］的降低，储能系统整体经济效益上升。当储能电池成本高于3 000元/(kW·h)时，储能系统投资规模不经济。储能电池成本降为2 500元/(kW·h)时，随着储能系统规模的增大，储能投资的年收益随之增大，表明储能成本降至该值时，储能系统的投资具备规模经济性。

图5 不同储能系统成本下的经济效益Fig.5 Economic benefits under different costs of energy storage system

(2)投资者角度。对投资者而言，储能系统的间接效益体现为储能项目的政府补贴，因此不考虑目标函数中储能系统的间接效益，仅从直接效益、政府补贴和储能系统成本进行经济效益评估。峰谷价差与储能项目的收益直接相关，政府补贴为500元/kW时，不同峰谷价差下储能系统年收益如图6所示。

图6 不同峰谷价差下储能系统年收益Fig.6 Annual revenue of energy storage system under different peak-valley difference

图6(a)为储能电池成本等于4 500元/(kW·h)时，不同峰谷价差下储能系统的年收益。峰谷价差K小于2元/(kW·h)，储能项目的投资不经济;峰谷价差大于2元/(kW·h)，投资具备规模经济性。

图6(b)为储能电池成本等于2 500元/(kW·h)时，不同峰谷价差下储能系统年收益。峰谷价差小于1元/(kW·h)，储能项目的投资不经济;峰谷价差大于1.5/(kW·h)，投资具备规模经济性。

4 结论

(1)用于电网削峰填谷时，电网调峰量不同，储能系统的功率、容量也随之不同。储能系统功率值取决于系统调峰量的大小，容量值与峰值负荷的持续时间有关。

(2)在本文算例中，当储能系统功率为峰值负荷的3.4%时，储能系统达到最大经济效益。

(3)在现有的技术水平下，锂离子电池储能系统实现规模化应用，电池成本需降到2 500元/(kW·h)。

(4)为实现储能技术的大规模发展，不仅需要厂商加大研究力度，提高储能系统的技术性能，降低生产成本;而且需要政府出台相关政策，支持储能产业发展。

［1］张恒良，谢诞梅，刘静宇，等.调峰机组启停优化控制［J］.热能动力工程，2005，20(5):300-303.

［2］余欣梅，熊信艮，吴耀武，等.电力系统调峰电源规划优化模型探讨及其应用［J］.中国电力，2003，36(1):48-51.

［3］曹昉，张粒子.结合系统调峰容量比确定抽水蓄能机组装机容量的方法［J］.电力自动化设备，2007，27(6):47-50.

［4］杨瑞瑜.九评:我国电网谷电大规模储能调峰技术路线［J］.电网与清洁能源，2012，28(4):1-11.

［5］谢俊，白兴忠，甘德强.水电/火电机组调峰能力的评估与激励［J］.浙江大学学报:工学版，2009，43(11):2079-2084.

［6］张文亮，丘明，来小康.储能技术在电力系统中的应用［J］.电网技术，2008，32(4):136-142.

［7］梁亮，李建林，惠东.大型风电场用储能装置容量的优化配置［J］.高电压技术，2011，37(4):930-936.

［8］鲍冠南，陆超，袁志昌.基于动态规划的电池储能系统削峰填谷实时优化［J］.电力系统自动化，2012，36(12):11-16.

［9］Oudalov A，Cherkaoui R ，Beguin A.Sizing and optimal operation of battery energy storage system for peak shaving application［C］//IEEE Proceeding of Power Tech，2007:299-303.

［10］孔飞飞，晁勤，袁铁江，等.用于短期电网调度的风电场储能容量估算法［J］.电力自动化设备，2012，32(7):21-24.

［11］王成山，于波，肖峻，等.平滑可再生能源发电系统输出波动的储能系统容量优化方法［J］.中国电机工程学报，2012，32(16):1-8.

［12］杨水丽，惠东，李建林，等.适用于风电场的最佳电池容量选取的方法［J］.电力建设，2010，31(9):1-4.

［14］Hans Bludszuweit，José Antonio，Domínguez Navarro.A probabilistic method for energy storage sizing based on wind power forecast uncertainty［J］.IEEE Transactions on Power Systems，2011，26(3):1651-1658.

［14］Wang X Y ，Vilathgamuwa D M.Determination of battery storage capacity in energy buffer for wind farm［J］.IEEE Transactions on Energy Conversion，2008，23(3):868-878.

［15］Li Q，Choi S S，Yuan Y，et al.On the determination of battery energy storage capacity and short-term power dispatch of a wind farm［J］.IEEE Transactions on Sustainable Energy，2011，2(2):148-158.

［16］杨裕生，程杰，曹高萍.规模储能装置经济效益的判据［J］.电池，2011，41(1):19 －21.

［17］Chengke Zhou，Kejun Qian，Malcolm Allan，et al.Modeling of the cost of EV battery wear due to V＆G application in power systems［J］.IEEE Transactions on Energy Conversion，2011，26(4):1041-1050.

［18］谭靖，李国杰，唐志伟.基于压缩空气储能的风电场功率调节及效益分析［J］.电力系统自动化，2011，35(8):33-37.

［19］韩勇，田闻旭，谭忠富.基于长期边际成本的不同电压等级输配电价定价模型及其应用［J］.电网技术，2011，35(7):175-180.

［20］谢瑛，谭忠富，程晋，等.节能减排调度环境下燃煤电厂发电成本分析［J］.电网技术，2011，35(2):137-142.