Arrhenius活化能理论的修正*

2013-02-13刘国杰黑恩成

大学化学 2013年2期

关键词：振子常数活化

刘国杰黑恩成

(华东理工大学化学系上海200237)

在描述化学反应速率随温度变化时，所有物理化学教材都会提及Arrhenius方程:

式中k为反应速率常数，Ea为Arrhenius活化能，R为摩尔气体常量，T为热力学温度。这个方程也可表示为:

式中A称为指前因子。据此，Arrhenius活化能被定义为:

1 Arrhenius理论

实际上，式(1)是个经验式，是Arrhenius引申了Van't Hoff方程并作了简化所得［1］。他为了从理论上证明这个方程，提出了如下4个假设［2-3］:

假设一:并不是所有分子都能反应，参与反应的只有那些能量较高的活化分子，一般分子必须在吸收了一定的能量后才能变成活化分子。根据这个假设，化学反应是按如下模式进行的:

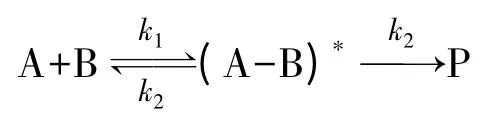
式中A和B是两个反应物分子，(A-B)*是活化分子对，P是反应产物。

假设二:分子活化成活化分子或活化分子对是一个可逆反应，且活化分子或活化分子对很容易放出Ea而变成一般分子。意即活化分子或活化分子对的浓度很低，它与一般分子间可近似视为处于化学平衡，因此有:

假设三:活化分子或活化分子对转变成产物P的速率很慢，这一步是速率控制步骤，故有:

化学反应的速率常数为:

假设四:活化分子或活化分子对转变成产物P的速率是不随温度而变的，意即k2是与温度无关的常数。因此，

式(8)代入了Van't Hoff方程，式中ΔrUӨm是一般分子转变成活化分子或活化分子对时系统标准摩尔热力学能增量，其值被认为Ea。所以，

这便是Arrhenius方程，式中Ea称为Arrhenius活化能，其物理意义为1mol一般分子变成活化分子或活化分子对所必须吸收的能量。

2 Arrhenius理论的修正

Arrhenius理论虽然简洁明了，但假设四却令人费解，既然活化分子或活化分子对转变成产物的速率很慢，它的反应速率常数k2怎么会不随温度而变呢?倘若k2是随温度而变的，那么，由式(3)定义的Arrhenius活化能Ea还会是活化1mol一般分子所必须吸收的能量吗?本文便是带着这样的疑问来考察Arrhenius理论的。

根据化学反应的过渡状态理论，上述反应模式也可表示为

式中(A…B)≠为活化络合物，它与反应物A和B间有化学平衡关系，式中的K≠c为平衡常数，即:

ν为活化络合物的分解频率，故该反应的速率为:

反应速率常数为:

现在，比较式(6)与式(11)便可明白，Arrhenius理论中的k2就相当于分解频率ν。因此，只要考察ν是否是温度的函数就行了。

按照过渡状态理论，这个分解频率ν是指活化络合物分子沿着反应坐标的不对称伸缩振动频率，由于化学反应速率只与这个振动频率有关，故不妨将活化络合物分子视为一个特殊的单维简谐振子，当能量标度的零点设在基态能级时，这个简谐振子的能量可用下式表示:

式中υ为振子的振动量子数，其值可取0，1，2…，代表振子的不同能级;式中h为Planck常量。显然，振子或活化络合物分子可以分布在它的各个可及能级上，故N个振子或活化络合物分子的平均能量为［4］:

式中〈υ〉为振子的平均振动量子数。由于活化络合物分子与反应物分子处于化学平衡中，它们在能级中的分布应服从Boltzmann分布，故由统计力学可得:

式中kB为Boltzmann常量，q0V为振子的能量标度零点设在基态能级上时的配分函数，其可表示为:

将式(15)代入式(14)，可算得:

比较式(13)和式(16)，可得:

已知形成活化络合物分子的化学键是一种很弱的离域键［5］，其力常数很小，振动频率很低，故ehν/kBT≈1+hν/kBT，将它带入式(17)，可进一步简化为:

所以，活化络合物分子的分解频率当为:

这是由于〈υ〉与可及振子的能级有关，温度越高，振子的可及能级越多，〈υ〉的值越大，故〈υ〉的值是温度的函数。本文假定这个函数可用温度的幂次表示，这样分解频率便与Tn成比例，β为比例系数。于是，上述Arrhenius理论中的活化分子对转变成产物的反应速率常数即为:

可见，k2并非常数，而是温度的函数。

现在，将式(7)改写成ln(k/k2)=ln{Kc}，并将它对温度求导，然后，代入Van't Hoff方程，则得:

式(22)便是本文对Arrhenius活化能理论修正的结果。式中B和n是两个与温度无关的常数;E是温度的弱函数，在关联实验数据时，也可视为常数。

式(22)虽有3个可调参数，但相比于原始的Arrhenius方程(式(2))，式(22)适用的温度范围要宽得多，对于较准确的动力学实验数据，需要应用这个方程，几乎在所有物理化学教材中都有这方面的介绍。

若将式(22)代入Arrhenius活化能定义式(3)，则不难得到:

式(23)表明，Arrhenius活化能Ea是由两部分组成。第一部分为一般分子转变成活化分子或活化分子对时系统的标准摩尔热力学能增量即E，这一部分是名副其实的活化能，它是使一般反应物分子活化所需的能量。第二部分是nRT，由上述推导可知，它是活化分子或活化分子对转变成产物时所吸放的能量，这部分能量与分子的活化没有关系。因此，Arrhenius活化能是系统发生化学反应所需的总摩尔能。有的教材认为，E相当于0K时的活化能，意即在加上nRT后，便是热力学温度T时的活化能。这种看法是值得商榷的，其理由是Arrhenius活化能的定义式(式(3))是不严格的，它是在假定k2是个常数，也即活化分子或活化分子对转变成产物时不吸放能量的情况下获得的。这在一般情况下是不适合的。