基于图像校正与相位相关的视频拼接算法

梁玉敏，蔡晓东，张学敏

(桂林电子科技大学 信息与通信学院，广西 桂林541004)

责任编辑:任健男

图像拼接技术主要考虑图像之间的配准与融合，图像可以由不同相机在不同时间、不同条件下拍摄得到，主流的算法主要有以下两大类[1-2]:

1)基于特征的拼接[3-4]的方法，提取了图像的显著特征，从而极大地压缩了图像的信息量、减少计算量。然而由于它只利用了一部分图像的信息，因此对于特征提取和匹配的错误就更为敏感，拼接的效果很大程度上依赖于特征点的选取以及匹配。这种方法特别不适用于特征较少、场景单一的环境。

2)基于变换域的图像配准方法[5]，根据傅里叶变换将图像由空域转换到频域上，在图像的频域中进行图像匹配，再由傅里叶逆变换获得图像在空域中相应的变换参数。这种方法对于两幅图像之间只具有平移的情况具有较好的效果，对于图像间存在旋转和缩放的情况，就需要采用对数极坐标变换将旋转和缩放量转换为平移量处理，这种反复的空域和频域变换影响了配准的效率。

通过上述两类算法的优缺点分析，本文针对摄像机安装位置固定的情况下，提出了摄像机标定与相位相关算法相结合的拼接算法。摄像机标定通常被用于三维重建[6]，三维重建通过标定来确定两幅图像之间的对应关系，而图像拼接配准最主要的目的也就是得到两幅图像间的对应关系，运用这种方法，就不需要依赖于由场景特征来确定两幅图像间的匹配关系。通过标定求得的摄像机参数对图像进行校正，使得两幅图像之间只存在平移关系，只要利用傅里叶变换中的平移特性，就可以快速地对两幅图像进行配准，从而避免了基于变换域方法中复杂、反复的对数极坐标的运算，大幅提高运算效率。

1 算法流程

本文提出的算法流程如图1所示。

首先在预处理阶段进行摄像机标定，获得摄像机的内外参数，从而完成待拼接图像坐标系到基准图像坐标系变换模型的求解，对图像进行畸变矫正，同时对图像之间存在的旋转、缩放进行调整。

再利用相位相关的方法将摄像机标定调整后输出的待拼接图像转换到基准坐标系，确定重合区，将重合区的图像进行融合处理，最终实现两幅图像的拼接。

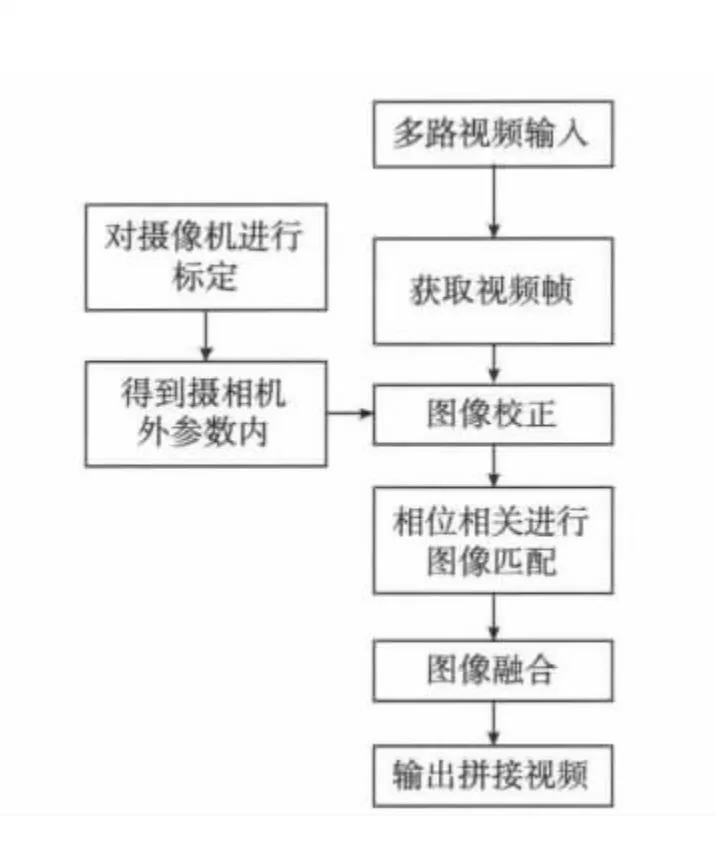
图1 算法流程图

2 关键算法描述

2.1 摄像机标定

本文算法中引入摄像机标定的目的主要有:1)通过标定的方法对摄像机输入的图像进行矫正，去除因为镜头引起的畸变;2)求解2台摄像机的位置关系，将图像校正在同一水平位置，使得2幅图像之间只具有平移关系，为后续的相位相关算法做准备。因此，这也是本文拼接算法中至关重要的一环。摄像机标定发展到今天已经形成了许多比较成熟的算法[7-8]。

本文使用棋盘标定的方法，在标定的过程中要求解4个内参数(fx，fy，cx，cy)和5个畸变参数，包括3个径向(k1，k2，k3)和2个切向(p1，p2)。对于畸变参数，理论上需要已知模式的3个角点所产生的6组信息来求解。对于棋盘6个不同视场图像需要3个旋转参数(ψ，φ，θ)和3个平移参数(Tx，Ty，Tz)。所以在每个视场中，就必须计算4个内参数和6个外参数。假设有N个角点和K个棋盘图像，K个棋盘图像提供2NK个约束，忽略畸变参数，有4个内参数和6K个外参数，有解的前提是2NK≥6K+4，或等价表示为(N-3)K≥2，其中图像个数K必须满足K＞1。这就是说3×3的棋盘最少需要2个视场来求解标定问题。考虑到噪声和数值的稳定性要求，得到高质量的结果，至少需要10幅7×8或者更多更大的棋盘图像。

本文实验中采用的是9×7个黑白相间的方格棋盘作为标定模板，其中每个方格的边长为53 mm。实验中使用2台工业应用的CCD摄像机输出的是704×576，将摄像机水平平行摆放，左右两边摄像机同时采集标定板的不同位置的图像，共计15组(采集图像位置越多，标定结果越精确)。如图2所示，从图像中可以看到，图像边缘房梁的弯曲就是由于摄像机镜头畸变引起的。

图2 摄像机的原始图像

假定求解标定参数时摄像机没有畸变。对每个棋盘视场，都有一个单应性矩阵H=[h1h2h3]，世界坐标系中的点Q映射到成像仪上点q可以单应性表示为:，其中H可以设置为等于摄像机内参数矩阵M乘以旋转向量和平移向量的组合矩阵，再加上缩放因子s，表示为

由于旋转向量是相互正交的，将缩放因子提到外边，则有r1和r2正交，由正交向量的性质可知r1和r2满足:r2=0且r1=r2。那么就可以得到2个约束关系

由此即可推导估计出摄像机的内外参数。若考虑到透镜畸变，假设针孔模型是完美的，令(x，y)为点的位置，(xd，yd)为畸变位置，那么就有

根据透镜畸变建模的方法[10]，对公式中的值进行替换，即可得到没有畸变的标定结果

重新估计内外参数之后，即可从这些大量的方程中得到畸变参数。通过求取这些内外参数，就可以计算出左右视图的校正查找映射表。通过目标图像上的每个整型的像素位置，首先找出对应于原始图像上的浮点位置，再利用周围源像素的整形值差值出新的值来，就可以得到经过校正后的效果如图3所示。与摄像机原始图像相比较，可以明显地看见图像边缘因摄像机镜头引起的弯曲畸变，经过标定处理之后变得平直。

2.2 相位相关图像配准

图3 左右两边摄像机经过标定校正的图像

经过对镜头畸变的矫正以及图像的位置校正得到的输出图片就只具有平移关系，因此可以利用相位相关方法进行图像匹配。

相位相关算法是配准两幅图像平移失配的典型方法。最早于1975年由Kuglin和Hines提出[11]，具有场景无关性，能够将纯粹的二维平移的图像精确配准。

当图像之间只具有平移关系时，相位相关可以简单描述如下:假设F1(u，v)和F2(u，v)分别为f1(u，v)和f2(u，v)的傅里叶变换，它们的互功率谱为

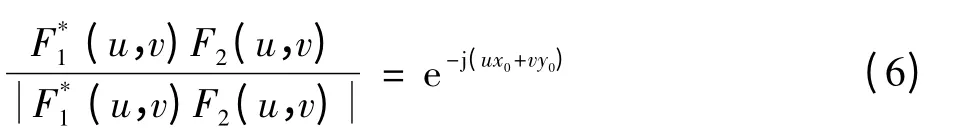
当图像中同时出现平移、旋转和缩放时，相位相关算法就会失效，因为由理论推导[9]可知无法获得脉冲函数。为了避免图像配准失败，同时避免文献[12]中复杂的坐标变换方法，首先由摄像机标定得到的旋转和缩放参数将两幅图像位置校正，使得两者之间只存在平移关系，再对校正后的图像进行配准。这样，就大幅度降低了算法的复杂度，快速地确定二维脉冲函数和求出高精度的平移参数，进而实现精确的配准。

3 实验结果

实验用的计算机主要参数有:英特尔酷睿双核E7400主频为2.8 GHz、内存4 Gbyte，使用Windows XP 32位操作系统。本文拼接算法在VS2008平台上通过C++编程实现。所用的摄像机输出的数字图像分辨率为704×576。

拼接中最常用的特征提取方法有SIFT，SURF等算法，文献[13]对SIFT，PCA-SIFT，SURF算法进行分析比较，对源图像进行尺度、旋转、模糊、亮度变化、仿射变换等变化后再与源图像进行匹配，经过实验得出:SIFT[14]在尺度和旋转变换的情况下效果最好，而SURF在亮度变化下匹配效果最好，而尺度和旋转的变化不及SIFT。因此在相同的场景下，将本文算法与基于SIFT特征提取的算法进行比较。

摄像机的原始图像如图4a和图4b所示，图中的数字表示两幅图像中相互匹配的特征点，图4c为SIFT算法拼接结果，图4d为本文算法的拼接结果，图像中较明亮的部分表示重叠区域。从图中可以看出，SIFT算法在相对单一的场景中正确提取的特征点较少，拼接图像的边缘依然存在畸变且图像重影明显。本文提出的拼接算法消除了由于摄像机镜头本身带来的畸变，同时较好地配准图像，但是为了校正2幅图像的位置，拼接图像损失了一部分边缘的像素。

图4 基于SIFT特征提取的拼接算法与本文拼接算法的效果对比

为了研究2幅图像的重合率对拼接的影响，改变2台摄像机夹角的大小，获取4组不同的图像重合率，以2个摄像机重合的画面范围为变量进行实验，得到的相位相关数据如表1所述。实验数据列表中相关系数经归一化即相同的图像相关系数为1，数值落在[-1，1]区间范围内。

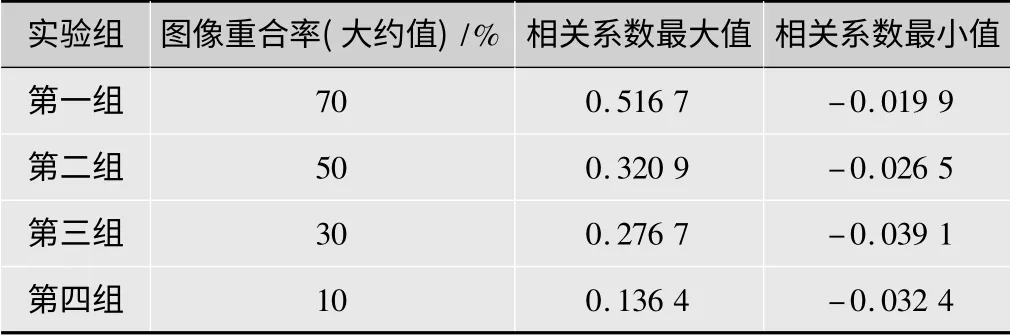
表1 图像重合率对相关系数的影响

由实验数据可以看出，当图像重合率上升时，互功率谱的峰值就越大，也越容易检测出更大范围的位移，从而更准确地确定平移位置，匹配也就越精确。

经过实验发现当图像重叠率低于30%时，无法进行配准，分析其原因主要有两个方面:第一，在预处理阶段进行相机标定时因为重合区域较少标定有一定的困难;第二，重叠率小于30%时相关系数的最大值不能从相关系数集合中明显的区分出来，也就无法确定图像平移位置。因此，本文设定一个相关系数最大值阈值，当计算得到的相关系数峰值超过预设的阈值时，再对图像进行拼接融合，如果低于阈值，就应调节摄像机位置提高重合率，重新进行计算。

基于该拼接算法工程的应用考虑，不选重合率为70%的图像，因为要获得同一分辨率的拼接图像，重合率越高，意味着需要更多的摄像机。折中考虑摄像机成本和拼接效率，选取重合率分别为30%和50%进行实验，得到2组拼接图如图5和图6所示。

从拼接效果来看，图像重合率50%的效果要比重合率30%的拼接效果好。30%的图像出现了一定程度的误匹配，如图5中矩形框的区域。

最后，实验取4组不同分辨率且只具有平移关系的图像输入进行测试，每组进行20次测试，求得平均处理时间如表2所述。

表2 图像分辨率和平均处理时间的关系

如果按照视频25帧/秒(f/s)，当数字图像分辨率超过1 280×720时就难以达到实时性的要求。因此实际应用中可根据需要选择分辨率相对较低的摄像机，通过多台摄像机来获得高分辨率的视频图像输出。

4 总结与展望

本文针对固定摄像机条件下，通过摄像机标定与相位相关图像匹配结合实现了实时视频的拼接。算法在预处理阶段通过相机标定获取图像旋转、缩放的变换矩阵，在实时处理视频的过程中直接进行矩阵运算，避免了复杂的对数极坐标变换和反复的FFT正向与逆向操作，使得算法处理速度有了极大的提高。特别是在场景特征单一的环境下，对鲁棒性特征选择与提取的依赖程度大大降低，与传统的基于特征的方法相比，具有明显的优势。同时运算速度与输入数字图像的分辨率成正比例关系，因此整套拼接系统具有较好的实时性和可控性。

而本算法的不足之处主要是在预处理过程中，摄像机标定的操作相对比较复杂，在摄像机相对位置改变后需要重新进行标定，缺乏一定的灵活性，如何找到一种自动快速准确的标定方法还需要进行相关研究。另外，图像拼接的效果在一定程度上依赖于2幅图像的重合率，在本文提出的算法中，2幅图像重合率在30%以上的情况下才会取得较好的结果，如何减少拼接对图像之间重合范围的依赖性还有待进一步研究。

[1]SZELISKI R，SHUM H.Creating full view panoramic image mosaics and environment maps[C]//Proc.ACM SIGGRAPH’97.Los Angeles:Addison Wesley，1997:251-258.

[2]SZELISKI R.Image alignment and stitching:a tutorial[M].[S.l.]:Handbook of Mathematical Models in Computer Vision，2006:273-292.

[3]宋海华，邵志一.基于改进型特征匹配的图像拼接方案设计[J].电视技术，2008，32(2):19-20.

[4]BROWN M，LOWE D G.Automatic panoramic image stitching using invariant features[J].International Journal of Computer Vision，2007，1(74):59-73.

[5]HUMBLOT F，COLLIN B，MOHAMMAD-DJFARI A.Evaluation and practical issues of sub-pixel image registration using phase correlation methods[C]//Proc.Physics in Signal and Image Processing(PSIP)Conference.Toulouse，France:[s.n.]，2005:115-120.

[6]HARTLEY R，ZISSERMAN A.Multiple view geometry in computer vision[M].2nd ed.Cambridge，UK:Cambridge University Press，2004.

[7]ZHANG Z Y.A flexible new technique for camera calibration[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，2000，22(11):1330-1334.

[8]戴玉超.立体视觉系统中定标、配准与三维测量研究[D].西安:西北工业大学，2008.

[9]LU YAN，PAYANDEH S.On the sensitivity analysis of camera calibration from images of spheres[J].Computer Vision and Image Understanding，2010，114(1):8-20.

[10]BROWN D C.Close-rang camera calibration[J].Photogrammetric Engineering，1971(37):855-866.

[11]KUGLIN C D，HINES D C.The phase correlation image alignment method[C]//Proc.the 1975 International Conference on Cybernetics and Society.[S.l.]:IEEE Press，1975:163-165.

[12]REDDY B，CHATIERJI B N.An FFT-Based technique for translation，rotation，and scale-Invariant image registration[J].IEEE Transactions on Image Processing and Remote Sensing，1996，5(8):1266-1271.

[13]LUO J，OUBONG G.A comparison of SIFT，PCA-SIFT and SURF[J].International Journal of Image Processing，2009，3(4):143-152.

[14]LOWE D G.Distinctive image features from scale-invariant key points[J].International Journal of Computer Vision，2004，60(2):91-110.