基于相似性度量优化的SIFT图像匹配算法

师 硕，于 明，于洪丽，阎 刚，薛翠红

(河北工业大学a.计算机科学与软件学院;b.国际合作与交流处;c.电气工程学院，天津300130)

责任编辑:任健男

SIFT(Scale Invariant Feature Transform)算法是Lowe在1999年提出的一种特征点提取算法[1]，此算法在图像局部特征研究过程中具有里程碑的作用。Lowe采用DoG(Difference of Gaussians)算法来快速求解高斯拉普拉斯空间中的极值点，加快了特征提取的速度，并在2004年对此算法进行完善总结，将特征点检测、特征矢量生成和特征匹配等过程完整地结合在一起进行优化[2]。SIFT算法对图像尺度变化和旋转变化具有不变性，并且对图像变形和光照变化有较强的稳定性，能够在光照、分辨率、图像畸形、旋转、压缩等变化的条件下，保证特征描述符不变，从而提高图像匹配的鲁棒性。因此，SIFT算法已被广泛应用到计算机视觉的诸多领域，如图像重建[3]、全景图拼接[4-5]及遥感图像配准[6]等。

虽然SIFT算法具有上述的优点，但其算法复杂，而且特征描述符是高达128维的特征向量，使得图像匹配时速度较慢，很难满足实时性要求。降低维数是解决SIFT算法匹配效率低的一种方法，Ke[7]等人在SIFT基础上提出了PCA-SIFT算法，首先利用主成分分析(PCA)算法对大量特征点的邻域梯度进行统计分析，生成低维的特征空间;然后把特征点的邻域梯度向量映射到生成的低维空间中，产生一个低维的描述向量，最终将128维高维特征降低到20维，提高了匹配效率。但PCA算法要求样本数据呈椭圆分布，且建立的是线性模型，对于非线性的高维数据，效果不及SIFT算法[8]。于丽莉[9]提出基于图像Radon变换的改进SIFT特征匹配算法，首先在图像的SIFT特征点区域内作一系列不同方向的直线，然后以这些直线上的图像Radon变换作为SIFT特征向量描述符并对其进行降维，文中最后得到24维特征描述符。但此方法中所用多条直线之间的夹角值的选取没有确定标准，因此不能判断降维后的特征描述符的最佳维度。本文在分析SIFT匹配过程的基础上，提出用街区距离和棋盘距离的线性组合来代替欧氏距离，作为特征描述符之间的相似性度量，在不影响算法鲁棒性的情况下，减少了匹配时间，提高了算法的效率。

1 匹配原理及常用距离

1.1 匹配的基本原理

当确定图像特征点并生成特征描述符后，就要按照相似性度量进行特征点匹配。适宜的相似性度量方法不仅能够提高匹配效果，同时还能降低度量算法的时间复杂度，通常采用相似距离来度量相似性。特征点匹配技术通常采用最近邻方法，即两组特征点集合中找到两两距离最近的特征点匹配对，理想状态这个匹配对对应的是场景中的同一个位置[10]。假定2幅图像中，基准图像P的特征点集合为Fp={p1，p2，…，pm}，其中m为特征点总数，待匹配图像Q的特征点集合为Fq={q1，q2，…，qn}，其中n为特征点总数，计算Fp集合中的每个特征点pi(i=1，2，3，…，m)与集合Fq中每个特征点qi(i=1，2，3，…，n)之间的距离。这样得到的最近邻并不能保证匹配正确，因此SIFT算法对得到最近邻距离和次近邻距离进行相除，发现当其比值小于0.8时，该匹配对是正确的可能性很高;反之，匹配对是错误的可能性很大，因此Lowe在文章中将此比值的判断阈值取0.8[2]。

1.2 常见距离

SIFT算法在匹配过程中采用欧式距离作为相似性度量。在n维空间中两点x和y的常见距离度量如下所述:

1)欧氏距离(Euclidean Distance，ED)，也称为L2范式，如式(1)所示

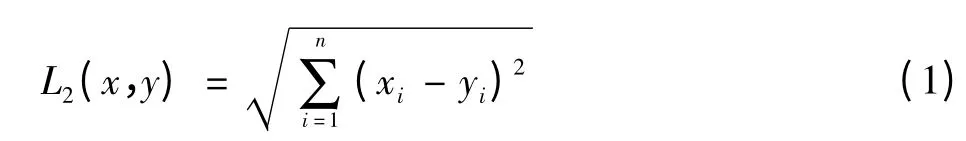
2)街区距离(City Block Distance，CBD)也称为曼哈顿距离，也称为L1范式，如式(2)所示

3)棋盘距离(Chessboard Distance，CD)，也称为切比雪夫距离，如式(3)所示

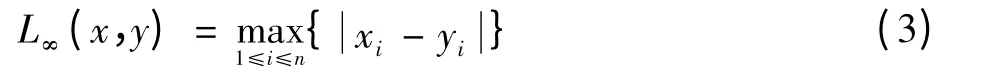
由式(2)、式(3)可知，计算L1和L∞比计算L2减少了乘法计算，可以提高效率。并且容易证明L∞≤L2≤L1[11]，若用L1直接代替L2，所得的值必偏大;用L∞直接代替L2，求得的值必偏小。因此采用L1和L∞适当的线性组合代替L2，这样既可以保证计算效率，又可以使计算偏差减少。

2 相似性度量优化

L1和L∞线性组合可以看成是n维空间中一些超平面的方程，这些超平面围成一个超多面体。因此计算L1和L∞线性组合代替L2，就可以看成是用相应的超多面体去逼近超球。根据文献[12]，可采用α(L1+L∞)和αL1+βL∞两种方式代替SIFT匹配中的欧氏距离。本文中将α(L1+L∞)和αL1+βL∞分别称为单系数法和双系数法。

2.1 单系数法度量优化

用α(L1+L∞)这种单系数的线性组合来代替L2，其中α是一个需要选择确定的实数。利用相应的超多面体去逼近超球来确定α，可分为如下情况:使超多面体恰在超球内部时，得到0.5为α的上确界;使超多面体恰在超球体外部，得到为α的一个下确界，其中n为维数;使超多面体与超球体面积相等，得到α的最优解，其表达式如式(4)所示

式中:n为维数。

因为SIFT特征描述符为128维，将128代入到式(4)中得到α=0.111 6为最优。α的最优解保证了单系数法作为相似性度量和欧氏距离具有相同的匹配正确率。

2.2 双系数法度量优化

L1和L∞还可以用αL1+βL∞这种双系数的线性组合代替L2，其中α，β是需要确定的实数。利用相应的超多面体去逼近超球来确定α和β，如式(5)所示

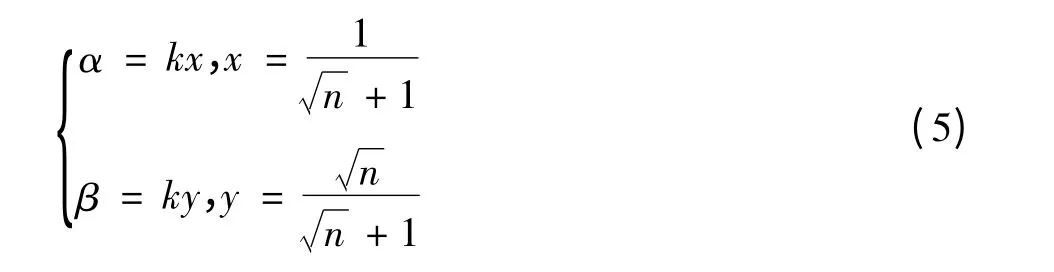
式(5)中k的值又分为如下三种情况确定:使超多面体恰在超球内部时，，此值为k的上确界;使超多面体恰在超球体外部时，k=，为k的下确界;使超多面体与超球体面积相等时，得到k的最优解，表达式如式(6)所示

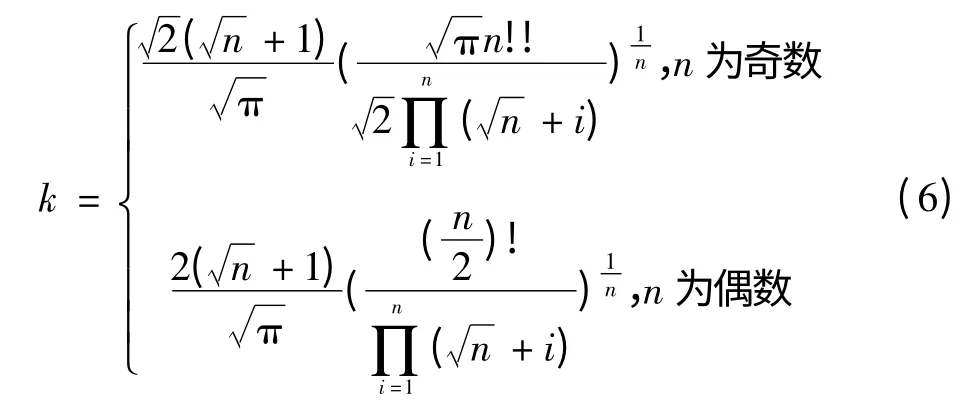
式中:n为维数。

将128代入式(6)计算得到k值，再根据式(5)，计算得α=0.086 749，β=0.981 448为最优解。α和β的最优解保证了双系数法作为相似性度量和欧氏距离具有相同的匹配正确率。

3 实验结果及分析

本实验采用Lowe提供的两组图像和一组自然光线不同焦距拍摄的图像进行实验，图像如图1所示，其中，图1a、图1b和图1c由Lowe提供，图1d和图1e是拍摄图像。采用MATLAB R2010a编程，运行在Intel Pentium Dual CPU 3.00 GHz和1 Gbyte RAM的计算机上，Window XP操作系统。

图1 实验图像

实验首先提取图像的SIFT特征点，然后对图1a和图1b、图1a和图1c、图1d和图1e以欧氏距离作为相似性度量进行匹配，再分别用单系数法α(L1+L∞)和双系数法αL1+βL∞代替特征点间的欧氏距离作为相似性度量，并且选用0.5，0.6，0.7，0.8作为最近邻和次近邻距离比值的判断阈值进行特征对提纯。结果表明在同一阈值下采用三种相似性度量匹配过程所得到的特征点数和特征对、匹配正确率都相同，但匹配时间不同，计算街区距离和棋盘距离的线性组合比计算欧氏距离用时短、效率高，并且双系数法稍快。不同阈值下匹配用时如表1所示。

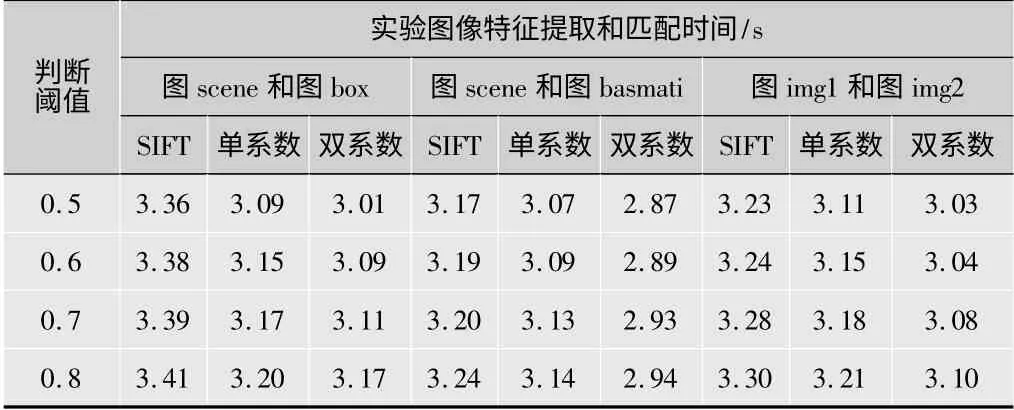
表1 不同阈值下匹配用时

所得特征点数和匹配对数随最近邻和次近邻距离比值阈值的增大而减少。比较发现，当阈值取0.6时，具有较好的匹配结果，三组图像阈值取0.6时匹配结果如图2所示。

图2 阈值为0.6时的匹配结果

因此，在不改变SIFT特征向量的生成过程，通过改变匹配过程中相似性度量计算方法，也能提高SIFT算法匹配的时间效率。

4 结论

本文在分析SIFT算法的基础上，研究了提高匹配效率的方法。在特征向量匹配过程中用棋盘距离和街区距离的线性组合代替欧氏距离进行图像匹配。实验结果表明，获得的特征点数和特征点对没有改变。因此，在保证SIFT算法的鲁棒性不变的情况下，有效提高了匹配效率。由于SIFT算法的可扩展性很强，但需要在各个尺度上进行计算，使其算法复杂，今后应研究改进SIFT算法来实现图像匹配的实时性。

[1]LOWE D G.Object recognition from local scale-invariant feature[C]//Proc.the Seventh IEEE International Conference on Computer Vision.Corfu，Greece:IEEE Press，1999:1150-1157.?

[2]LOWE D G.Distinctive image features from scale-invariant key points[J].International Conference of Computer Vision，2004，60(2):90-110.

[3]张志，叶蓬，王润生.基于SIFT特征的多帧图像超分辨重建[J].中国图象图形学报，2009，14(11):2373-2377.

[4]MATTHEW B，LOWE D G.Recognizing panoramas[C]//Proc.the Ninth IEEE International Conference on Computer Vision.Nice，France:IEEE Press，2003:1218-1225.

[5]何敬，李永树，鲁恒，等.基于SIFT特征点的无人机影像拼接方法研究[J].光电工程，2011，38(2):122-126.

[6]李芳芳，贾永红.利用线特征和SIFT点特征进行多源遥感影像配准[J].武汉大学学报:信息科学版，2010，35(2):233-236.

[7]KE Y，SUKTHANKAR R.PCA-SIFT:a more distinctive representation for local image descriptors[C]//Proc.the IEEE Computer Society Conference on Computer Vision and Pattern Recognition.Washington，DC:IEEE Press，2004:506-513.

[8]MIKOLAJCZYK K，SCHMID C.A performance evaluation of local descriptors[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，2005，27(10):1615-1630.

[9]于丽莉，戴青.一种改进的SIFT特征匹配算法[J].计算机工程，2011，37(2):210-212.

[10]王会峰，刘上乾，汪大宝.基于序列图像特征配准的摄像机旋转补偿算法[J].光学精密工程，2008，16(7):1330-1334.

[11]王晓华，傅卫平，梁元月.提高SIFT特征匹配效率的方法研究[J].机械科学与技术，2009，28(9):1252-1255.

[12]王钲旋，李海军，周春光.高维空间中用计算街区距离和棋盘距离的线性组合代替计算欧式距离[J].小型微型计算机系统，2004，25(12):2120-2125.