基于NMF和LS-SVM的肖像漫画生成算法研究

王海君，杨士颖，王雁飞

(上海大学 影视艺术技术学院，上海200072)

责任编辑:任健男

1 肖像漫画简介

肖像漫画是以人物为描绘对象，通过以形写神、联想等创作方法，着重刻划人物本身特定的外形特征和内在神韵，获得形神兼备的效果。随着数字媒体技术的飞速发展，对于绘制肖像画这种具有艺术性质的计算机仿真技术的研究，具有很大的意义。

文献[1]提出基于模板的肖像漫画夸张方法，但这种方法对样本要求比较高，而且夸张得不够明显。文献[2]提出将人脸数据与漫画数据分别利用PCA降维并通过SVM方法进行统计学习，这种方法忽略了人脸数据与漫画数据之间的相关性，最终生成的肖像漫画过度变形且不够协调。文献[3]提出可以将特征向量的变换用旋转、缩放和平移来表示，但是很难学习到肖像漫画的实际夸张特点。

肖像漫画的绘制过程主要包括形状夸张和上色，本文主要研究如何改善形状的夸张。将人脸的特征点记作Si，漫画的特征点记作Si'，本文的目标就是确定它们之间的相关性:Si'=f(Si)，基于统计学习的方法可以用来确定这个关系式。

针对上述问题，本文提出了一种基于NMF和LSSVM的肖像漫画生成算法，实验证明，该方法有效地学习到了肖像漫画的夸张变形特征，能够在夸张肖像主要特征的同时避免出现过度变形。同时，允许用户调节夸张参数的数值大小来调整生成的漫画效果。

2 非负矩阵分解(NMF)

NMF是一种新的矩阵分解算法[3]，该算法能够找到一个基矩阵U和一个系数矩阵V，从而将一个非负的矩阵分解为两个非负矩阵的乘积。相比传统的PCA和ICA，基于基矩阵组合的表示形式能够反映人类思维中“局部构成整体”的特点。NMF算法的基本思想如下:

给定非负矩阵A∈Rn×m，求解非负矩阵U∈Rn×r和V∈Rr×m，满足A=UV，其中U为基矩阵，V为系数矩阵。对于U和V，采用迭代算法获取，以欧式距离平方作为分解误差的约束测度函数，公式为

可以任意初始化U和V，通过以下迭代过程使得误差减小到稳定值

3 偏最小二乘支持向量机(LS-SVM)

LS-SVM发展自支持向量机(SVM)，训练数据的样本记为(xi，yi)，xi是输入向量，yi是目标值，目标函数在特征空间中被描述为

约束条件:yi=φ(xi)×ω+b+ξi，i=1，2，...，l。其中，φ(·)是核函数，矢量ω为权值矢量，ξi为误差变量，γ是惩罚因子，b是偏差。引入拉格朗日法解决核函数的优化问题，公式为

式中:ai，i=1，2，...，l是拉格朗日乘数。根据下列条件

可得

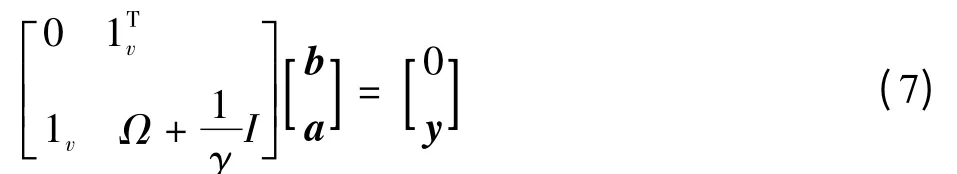
图1 算法流程图

式中:x=[x1，x2，...，xl]，y=[y1，y2，...，yl]，a=[a1，a2，...，al]，对称函数K(xk，xl)=φ(xk)Tφ(xl)，满足Mercer条件。

最小二乘支持向量机函数回归估计为

其中，a，b由式(7)求解出。

本文中核函数为径向基函数

4 基于NMF和LS-SVM的肖像漫画生成算法

4.1 算法流程

本文提出的算法主要包括训练阶段和应用阶段，如图1所示。在训练阶段，首先对样本手工标记特征点并归一化，然后通过NMF对夸张矩阵降维，利用LS-SVM统计学习夸张矩阵与人脸特征之间的关系，建立形状夸张模型。在应用阶段，利用AAM[4]提取输入肖像照片的特征点，根据之前已建立的形状夸张模型，得到对应的漫画特征点。应用薄板样条图像变形算法[5]对原始肖像变形并风格化，就生成最终的肖像漫画效果。

4.2 实验样本的选取及预处理

本实验所需要的数据库包括50个样本对，每个样本对包括一张正面肖像图像与对应的一张漫画图像。为了保证实验样本的统一性，只收集了某一位特定的漫画家的作品。然后对所有样本手工标记特征点，如图2所示。

针对此课题，在MPEG-4中标准人脸定义的基础上，为了降低计算量的同时保留漫画的夸张信息，在每个样本图片上标记了54个特征点。对眼睛、鼻子以及嘴巴采集了37个特征点，因为这些区域最能代表漫画的夸张细节，对脸的轮廓采集了17个特征点，对不能明显体现漫画夸张的区域，例如眉毛，没有采集特征点。

图2 夸张系数对肖像漫画夸张效果的影响

4.3 形状夸张模型的建立

对于一组样本{Si，S'i}，Si和S'i分别代表第i张肖像照片及对应的第i张夸张漫画的特征点，并将它们之间的差异向量记作ΔSi=Si-S'i，这里的ΔSi就是漫画家对人脸五官轮廓的夸张变形。

假设存在参数向量b使得ΔS=M(b)，那么可以通过改变参数向量b的数值来控制肖像漫画的夸张变形。为了解决这个问题，首先应用NMF方法来处理所有样本的差异向量ΔS。考虑到夸张向量ΔS会出现负值，将ΔS分成两部分:ΔS=ΔS+-ΔS-，其中和均为非负矩阵。这样任意样本数据ΔSi可以表达为

对式(7)非负分解可得

漫画与人脸之间的关系可以表述为

4.4 夸张系数对肖像漫画夸张效果的影响

在实验中，利用NMF算法将50个样本的差异矩阵ΔS降维得到5维的系数矩阵和以及相应的基矩阵和。通过改变和的不同数值，就可以得到不同的漫画夸张效果。图2中的第一行对应着5维夸张系数向量里单独的每一维，为了跟样本里的夸张效果保持一致，每维系数取值为3.0。同样的，第二行对应着夸张系数向量里单独的每一维，每维系数取值为3.0。

通过图2可以看出，将夸张矩阵分为正负两个部分后，最终非负分解得到的系数矩阵具有对称性。例如，当b-=(3，0，0，0，0)时，脸的下半部被缩小并上移，当b+=(3，0，0，0，0)时，脸的下半部被夸大并下移。可以从图2看出，漫画家也正是基于这几种夸张思路来画的肖像漫画。

4.5 夸张系数与人脸特征点之间的相关性

漫画家在画漫画时，针对不同的人脸会有不同的夸张变化，这在数学上就表现为不同的夸张系数数值。所以人脸特征点Si和夸张参数b+/-i 之间有很大的相关性。

由于漫画与人脸之间的关系可以表述为

如果统计出人脸特征点与夸张参数之间的关系为

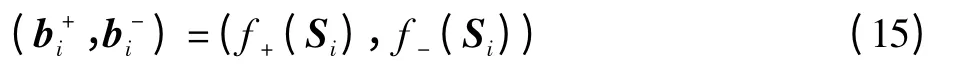
就可以对任意一张输入的正面人脸Snew输出漫画特征点，即

同样，对人脸特征数据也利用NMF降维，那么对于任意输入的一张人脸，可得到

式中:Y为人脸数据的基矩阵，c为对应的系数矩阵。那么式(12)可写成

式中:g+/-(cnew)=f+/-(Ycnew)。

5 算法实现及结果分析

5.1 应用LS-SVM统计夸张参数与人脸特征点之间的相关性

为了验证算法的有效性，本文以Windows7为系统平台，通过MATLAB7.8.0(R2009a)进行仿真实验。实验中利用NMF将人脸特征点数据由104维降低到10维，夸张矩阵由104维降低到5维，按照图1的流程采用LS-SVM算法来统计学习式(14)，以便根据人脸特征点Snew来求得对应的肖像漫画的特征点Snew'，实验结果如图3所示。

图3 本文算法与其他算法的结果对比

5.2 算法实现结果及分析

对于本文算法，将人脸照片(如图3a)输入到形状夸张模型中，默认得到夸张系数的数值为下:b+=(2.2，0.3，0.1，3.1，0.4)，b-=(0.2，5.2，1.3，0.1，1.2)。根据式(10)可以求出相应漫画人脸的特征点，经过薄板样条算法变形并风格化后的图片如图3d所示。作为效果对比，图3b为文献[2]中的夸张方法得到的结果，图3c为文献[7]中的方法处理得到的结果，可以看出，这两种算法虽然可以将人脸形状进行夸张，但是会出现夸张过度的情况，夸张结果不协调。本文算法却能够在合理地夸张主要特征的同时有效避免出现过度变形。说明相比文献[2]中利用PCA降维数据，NMF算法具有更好的效果。

相比于其他算法，本算法还具有的优势是用户可以通过调整夸张系数的数值来调整最终的漫画效果，如图4所示。在本实验中，通过调整夸张系数数值，来得到不同的夸张效果。图4中第二行为夸张系数b-的取值，第三行为夸张系数b+的取值，图3a为原图，图3b、图3c、图3d为以不同的夸张系数的取值最终生成的效果图。

6 结束语

本文提出了基于NMF和LS-SVM的肖像漫画夸张算法，该算法可以合理地夸张主要特征并避免出现夸张不协调的情况。在未来的工作中，研究重点包括改进夸张系数与人脸特征点之间的统计模型，研究漫画风格与夸张系数之间的关系，即用户可以通过选择预设定的多组夸张参数来得到满意的夸张效果。

图4 不同夸张系数数值的夸张结果

[1]LIANG Lin，CHEN Hong，XU Yingqing，et al.Example-based caricature generation with exaggeration[C]//Proc.the 10th Pacific Conference on Computer Graphics and Applications.[S.l.]:IEEE Press，2002:386.

[2]LIU J，CHEN Y.Mapping learning in eigenspace for harmonious caricature generation[C]//Proc.14th ACM International Conference on Multimedia.Santa Barbara:IEEE Press，2006:683-686.

[3]LEE D D，SEUNG H S.Learning the parts of objects with nonnegative matrix factorization[J].Nature，1999(401):788-791.

[4]COOTES T F，EDWARDS G J，TAYLOR C J.Active appearance models[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，2001，23(6):681-685.

[5]BOOKSTEIN F L.Principal warps:thin-plate splines and the decomposition of deformations[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，1989，11(6):567-585.

[6]LIU J，CHEN Y，XIE J，et al.Semi-supervised learning of caricature pattern from manifold regularization[EB/OL].[2012-12-20].http://link.springer.com/chapter/10.1007%2F978-3-540-92892-8-42 page-1.