一种联合特征参数的信号调制识别算法
2013-02-13黄国策
吴 涛,黄国策
(空军工程大学 信息与导航学院,陕西 西安710007)
责任编辑:许 盈
信号调制类型识别在认知无线电中是一项重要的任务。在接收端没有发送数据先验信息(比如信号功率、载频、相移等)时盲调制识别是一件困难的任务。信号调制类型识别算法可以被分为两类:基于最大似然的算法和基于特征的算法[1]。前者实现复杂,并且对模型的时间偏移、相位偏移、频率偏移和相位噪声等很敏感。后者实现容易,并且如果特征选择合适时有一定的鲁棒性[1-2]。然而许多具有一定鲁棒性的信号特征计算复杂度却很高,如循环谱、高阶累积量和小波变换等。尽管这类算法中有一些快速算法,但运算量仍然很大[3-7]。由于这些问题,利用少量计算简单的参数进行信号调制类型识别是很有前景的。文章介绍了几种信号特征参数,提出了一种使用信号分形盒维数和归一化峰度作为信号特征参数的算法(Dimension-Peak,DP)。
1 分形盒维数和归一化峰度
假设接收信号x(t)是调制信号s(t)和高斯白噪声n(t)的叠加,即x(t)=s(t)+n(t)。其中,n(t)~N(0,σ2)。在仿真中,s(t)属于以下6种调制类型:ASK,4FSK,8PSK,16QAM,4PAM和OFDM。其中OFDM信号子载波采用BPSK调制,子载波数为64。信号调制类型识别的目标是对于给定的s(t)的N个信号采样点,在集合ASK,4FSK,8PSK,16QAM,4PAM和OFDM中识别分类。
1.1 分形盒维数
分形维数是分形理论中定量描述分形集复杂性的主要参数。分形维数能有效度量通信信号。Hausdorff维数是分形理论中最基本的一种分形维数,但其计算复杂,因此,一般使用分形盒维数描述信号的分形信息。文献[1]提出了一种基于分形盒维数的调制类型识别的方法。
图1是ASK,4FSK,8PSK,16QAM,4PAM,OFDM六种调制信号的分形盒维数随信噪比变化的曲线图。横轴SNR代表信噪比,纵轴DIM代表信号分形盒维数。从图1中可以看出,ASK,4PAM,8PSK,16QAM调制信号归一化峰度随着SNR有明显变化,当SNR变高时,逐步趋于稳定。4FSK和OFDM信号不随SNR变化而变化,两者分形盒维数特征类似。从图1可以看出在SNR未知时,分形盒维数很难区分信号类型。在SNR已知时,4FSK信号和OFDM信号也不能依赖分形盒维数区分。
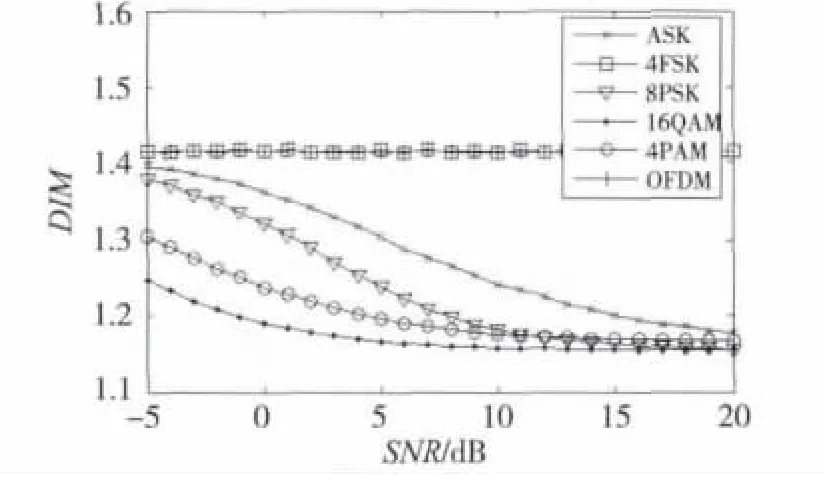
图1 信号分形盒维数
1.2 归一化峰度
归一化峰度等于3的实信号是高斯信号,小于3的实信号是亚高斯信号,大于3的实信号为超高斯信号[8]。无线通信中的数字调制信号多为亚高斯信号。图2是ASK,4FSK,8PSK,16QAM,4PAM,OFDM六种调制信号的归一化峰度随SNR变化的曲线图。横轴SNR代表信噪比,纵轴K代表信号归一化峰度。从图2中可以看出,4PAM、16QAM调制信号归一化峰度在不同SNR下的变化。ASK和OFDM信号不随SNR变化而变化,两者信号特征类似。4FSK和8PSK信号特征类似,且随着SNR变化而变化。由图2可以看出,信号归一化峰度用于区分信号调制类型时,在SNR未知时不能有效区分。在SNR已知时,也不能区分4FSK和8PSK信号,以及ASK和OFDM信号。
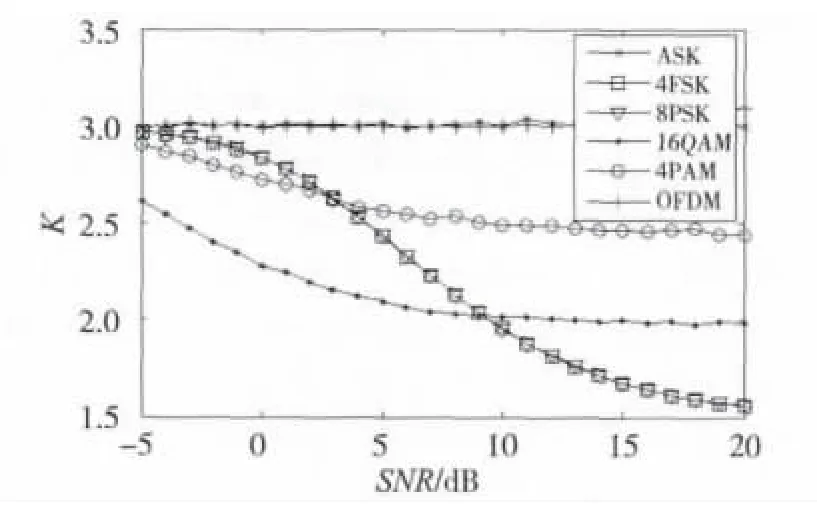
图2 信号归一化峰度
2 Dimension Peak算法
从图1和图2可以看出,分形盒维数和归一化峰度都在SNR未知时不能有效区分信号调制类型。DP算法将分形盒维数和信号归一化峰度作为二维信号特征向量,使用径向基神经网络进行分类识别。
分形盒维数在文献[9]中定义为
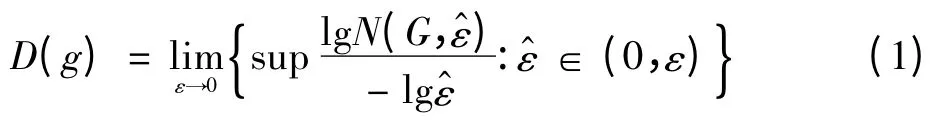

则分形盒维数可以表示为

实信号的归一化峰度为

式中:E[x]为x的期望。
图3和图4分别是是信号信噪比大于-5 dB和0 dB时,ASK,4FSK,8PSK,16QAM,4PAM,OFDM六种调制信号的二维特征图。图中实验信号SNR分别是在-5~+20 dB和0~+20 dB均匀分布的。由图3和图4可以看出,相对于一维的分形盒维数特征或归一化峰度特征,二维特征具有更明显的信号调制类型区分能力。由图3和图4对比可以看出,信号在SNR较高时,信号具有更明显的分类特征。当SNR接近-5 dB时,信号特征出现聚集现象,不利于区分。然而,相对于前面两种一维特征,新算法在区分信号调制类型时不需要已知SNR。


3 仿真验证
待测 信 号 为ASK,4FSK,8PSK,16QAM,4PAM,OFDM六种数字调制信号。实验中,待测信号信噪比为在20 dB>SNR>-5 dB和20 dB>SNR>0 dB范围内进行测试。由于SNR很高时,信号特征明显,容易区分,所以实验时SNR取值上限为20 dB。SNR>-5 dB时每种信号测试2 600次,SNR>0 dB时每种信号测试2 100次。两种测试的径向基神经网络分别由SNR在-5~+20 dB和0~20 dB的6种随机数据调制信号训练。表1和表2分别是SNR>-5 dB和SNR>0 dB时调制信号分类结果。其中No.1,No.2,No.3,No.4,No.5和No.6分别代表检测结果为ASK,4FSK,8PSK,16QAM,4PAM和OFDM信号。表中的数据代表相应的检测次数。由表1和表2知,在SNR>-5 dB时,6种信号的分类正确率分别是95.46%,94.31%,97.42%,100.00%,99.85%,98.96%。在SNR>0 dB时,6种信号的分类正确率都超过99.90%。可见,新算法在SNR未知时检测性能也很高。但该算法的缺点是在SNR很低时,性能会下降。
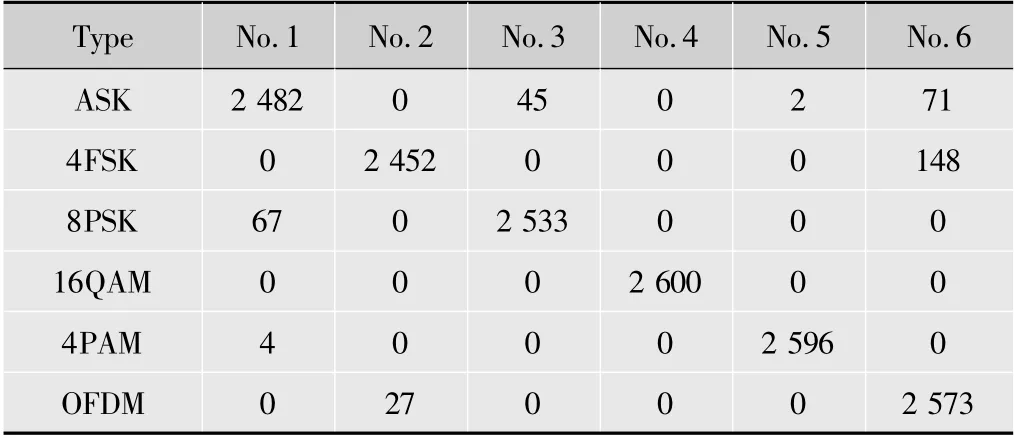
表1 SNR>-5 dB时分类结果
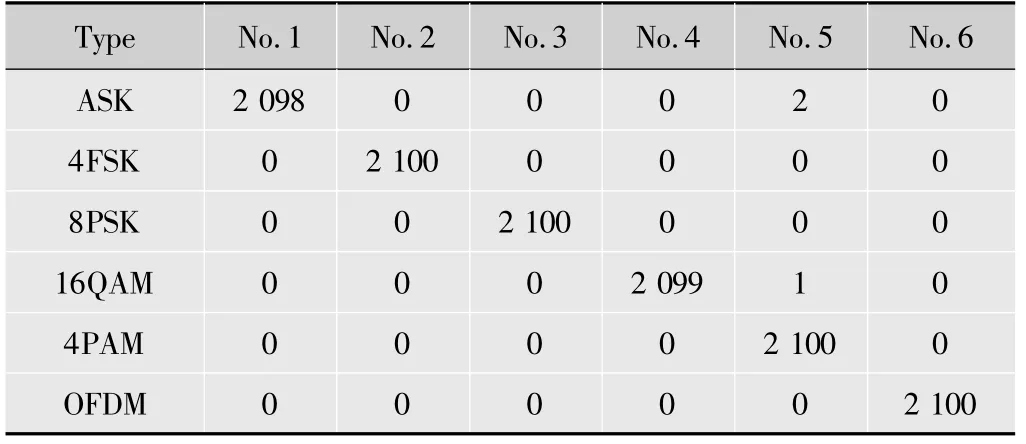
表2 SNR>0 dB时分类结果
4 结论
分形盒维数和信号归一化峰度作为信号特征,它随着SNR变化而变化。DP算法使用分形盒维数和归一化峰度作为二维分类特征,并使用神经网络作为分类器进行信号调制类型识别。该算法具有计算简单、实现容易的特点。仿真结果表明,在SNR>-5 dB时,DP算法在SNR未知的情况下,可以取得很高的检测性能。
[1]DOBRE O A,ABDI A,BARNESS Y,et al.A survey of automatic modulation classification techniques:classical approaches and new developments[J].IET Commun.,2007,1(2):137-156.
[2]RAMKUMAR B.Automatic modulation classification for cognitive radios using cyclic feature detection[J].Circuits and Systems Magazine,2009,9(2):27-45.
[3]DOBRE O A,ABDI A,BAR-NESS Y,et al.Cyclostationarity-based modulation classification of linear digital modulations in flat fading channels[J].Kluwer Wireless Personal Commun,2010,54(4):699-720.
[4]SHEN L,LI S,SONG C,et al.Automatic modulation classification of mpsk signals using high order cumulants[C]//Proc.8th International Conference on Signal Processing.[S.l.]:IEEE Press,2006:4.
[5]MENG Lingling,SI Xiujie.An improved algorithm of modulation classification for digital communication signals based on wavelet transform[C]//Proc.International Conference on Wavelet Analysis and Pattern Recognition.[S.l.]:IEEE Press,2007:1226-1231.
[6]VADIVELU R.Implementation of modified time-smoothing algorithms and its comparative analysis in spectrum sensing[J].European Journal of Scientific Research,2012,80(2):237-243.
[7]陈纬,张旭东,邢志强.基于综合检测的多调制格式信号频谱感知[J].电声技术,2013,37(3):63-38.
[8]张贤达.现代信号处理[M].2版.北京:清华大学出版社,2002.
[9]赵春晖,马爽,杨伟超.基于分形盒维数的频谱感知技术研究[J].电子与信息学报,2011,33(2):475-478.
[10]吕铁军,郭双兵,肖先赐.调制信号的分形特征研究[J].中国科学:E辑,2001,33(6):508-513.
