城市末端物流配送问题研究

何俊生，史 昊 HE Jun-sheng,SHI Hao

（重庆交通大学 交通运输学院，重庆 400074）

车辆路径问题 （Vehicle Routing Problem,VRP）在交通运输、工业生产等各领域应用广泛，目前基于VRP问题研究的成果很多，尽管对于该类问题的求解方法层出不穷[1-5]，其中不乏一些关于末端物流配送问题的管理学模型成果[6]，但是对于这类问题的量化研究成果尚未见文献报道。

末端配送是指送达给消费者的物流活动，是以满足配送环节的终端 （客户）为直接目的。随着社会经济活动越来越以消费者的需求为中心， “用户第一”的基本观念深入人心，因此末端物流越来越受到重视。能否快速送达是顾客衡量快递公司的一个重要标准。而末端物流配送需要考虑的很重要的一点则是最短时间配送路径，因此本文对这一问题进行深入研究。

1 城市末端物流配送路径模型

1.1 城市末端物流配送路径模型建立。为了不失一般性，将快递企业抽象为配送中心，将各个顾客抽象为配送节点。模型建立的目的是为了求得配送中心到各个需求节点的总配送时间最短。变量dij表示节点i到节点j的距离；若从i到j无路径到达则用dij=∞表示。变量vijTi（）表示Ti时刻车辆从节点i到节点j的行驶速度。变量tijTi（）表示从节点i到节点j所用的时间，同理，若从i到j无路径则用tijTi（）=∞表示；其中Ti表示到达节点i的时刻，从配送中心出发的时刻用T0表示。tijTi（）可用公式tijTi（）=dijvijTi（）计算得到。令物流配送中心某车配送的客户集合为N（其中0代表物流配送中心，配送节点的个数为n），Ti（）,i,j∈N为Ti时刻从i点出发到j点的最短行驶时间。则城市末端物流配送问题数学模型如下：

式 （2）到式 （6）为约束条件。xij为决策变量，意为判定节点i与节点j之间是否有可通行路径；如果节点i和节点j在可通行路径上i≠（）j，则xij=1，否则xij=0。式 （2）和式 （3）是平衡条件，表明路径的可逆性；式 （4）表示对每个节点的配送为一次且仅为一次，若为配送中心，则表示车辆离开配送中心后完成配送任务仍回到配送中心；式 （5）表示从节点j出发的时刻；式 （6）为确保配送回路通过配送中心。

1.2 城市末端物流配送路径模型的遗传算法。VRP问题属于NP-Hard问题，解决这类问题多用启发式算法。遗传算法是美国密执安大学Holland教授受生物模拟技术启发，创造出的一种适合于复杂系统计算优化的启发式算法。该算法具有较强的鲁棒性，广泛应用于车辆路径问题的寻优计算中，并在多数情况下能得到比较满意的解。1.2.1 编码。本文采用自然编码方式。例如有6个配送节点，其编号分为为1到6号。首先将需要配送的节点进行随机排列，如假设0为配送中心，这里可在染色体两边添加0，形成染色体；就形成了0与0之间的一条配送路径 （从配送中心出发，最后回到配送中心），即0→1→3→4→6→5→2→0。

通常的研究认为节点间由直线相连[7-11]，但更多情况下节点与节点间是由路网相连的，即从节点到节点的路径不唯一；因此单一的认为节点间由直线组成是不符合实际的，本文从节点间由路网组成出发，两点间的路网最短时间路径由Dijkstra算法求得。

1.2.2 适应函数。这里以目标函数作为适应函数，即完成一条配送路径所需的时间。个体所对应目标函数值Z即为此个体的适应值。

1.2.3 选择操作。取种群各染色体适应值倒数除以倒数之和，作为各染色体被选择的概率；采用轮盘赌的方式选择染色体复制到新种群，直到新种群规模与父代相同为止。

1.2.4 交叉、变异操作。本文采用部分映射交叉法，从种群第一个染色体开始，两两成组，对每组染色体，随机生成数若小于等于交叉概率pc，则染色体两端0不动，取中间随机一段进行交叉互换，否则，该组染色体不进行交叉操作。对于交叉操作，染色体若有与交叉区段冲突数字 （下划线表示）， 两染色体互相一一对应交换，交叉结束。例如：

变异操作是对种群每一个染色体，随机生成数若小于等于变异概率pm，则染色体两端0不动，随机取染色体两个数字并交换位置，形成新染色体，否则，该染色体不进行变异操作。

1.2.5 计算过程

Step 1：各参数初始化，并设置达到最大迭代次数gen max为算法终止条件；

Step 2：gen:=1时，随机产生初始群体chromgen；

Step 3：计算种群各个体的适应值，并选出得到最优的适应值和最优的个体；

Step 4：根据轮盘赌选择法，复制染色体生成新的种群；

Step 5：对新的种群进行交叉、变异操作；

Step 6：采用精英策略，取上一代最优个体替代新一代对应位置染色体；

Step 7： gen:=gen+1；

Step 8：若满足终止条件，转到step 9，否则转到step 3；

Step 9：取种群最优的适应值benefitgen即为最短时间，对应个体bestpopgen为最优方案。

2 算例分析

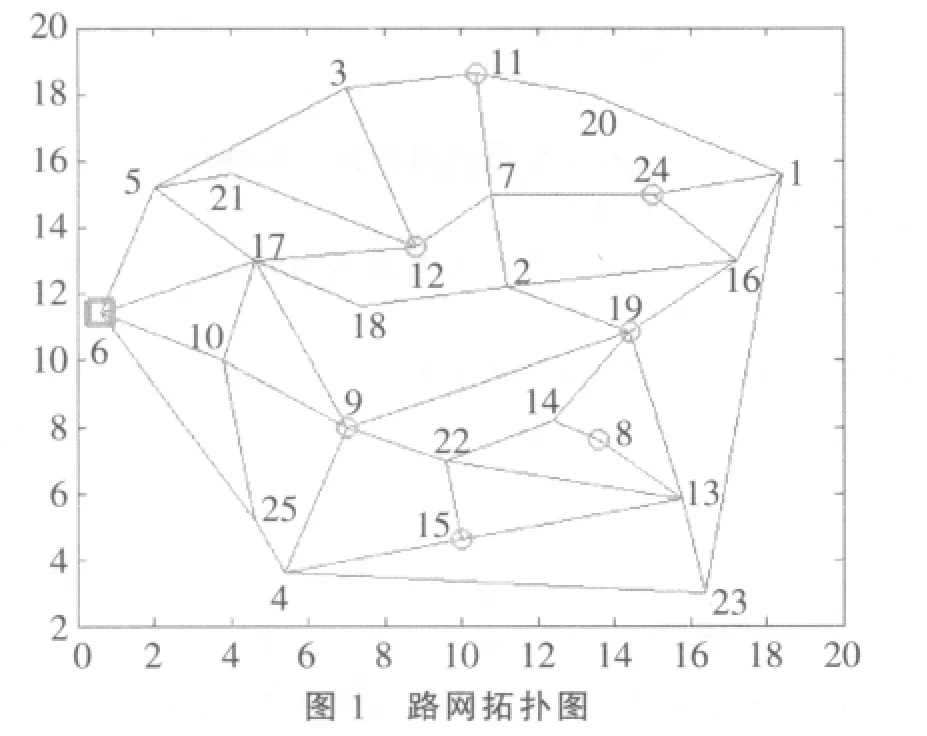
设路网中共有25个节点，利用random函数生成的随机点坐标如表1所示。由表1生成的路网拓扑图如图1所示。

其中的数字为各个节点编号，红色方块表示配送中心，紫红色圆形表示各个配送点。

考虑到实际情况，在不同时段不同路段的行车速度不同。故设所有路段在非高峰时段行车速度为40km/h，某些路段高峰时段 （7:30-9:00，17:00-19:00）平均行车速度如表2所示。

若上午8:00从节点6发车，设种群规模为40，迭代次数为100次。在CPU2.0GHz，内存2GB的计算机上多次利用遗传算法求出的最短时间为1小时54分钟，其中一条行驶路径为：6→17→12→3→11→7→24→16→19→14→8→13→15→22→9→10→6 （见图 2）。

3 结 论

本文讨论了实时路网下的一类直接面对消费者的末端物流配送问题，建立了末端物流配送路径模型。通过结合Dijkstra算法的优化遗传算法求得最优解，经过数值算例的验证，该模型更加符合物流配送的实际情况，该算法能在实时路网环境下有效地找到最短时间路径，减少车辆行驶的总时间。进一步的研究工作可以从多车辆路径实时路网末端物流配送路径建模及模型快速求解优化算法等方面展开。

[1] 孙国华.基于真实路网的车辆路径问题研究[J].物流技术，2011,30(1):43-45.

[2] 韩世莲.带时间窗的多目标配送线路选择问题的目标规划模型[J].物流技术，2008,184(1):44-45.

[3] 贺竹磬，孙林岩.动态交通下车辆路径选择模型及算法[J].交通运输工程学报，2007,7(1):111-115.

[4] Babak Farhang Moghadam,Seyed Mohammad Seyedhosseini.A particle swarm approach to solve vehicle routing problem with uncertain demand[J].International Journal of Industrial Engineering Computations,2010(1):55-66.

表1 路网节点坐标

表2 高峰时段路段拥堵平均行车速度

[5] Yiyo Kuo,Chi-Chang Wang.Optimizing the VRP by minimizing fuel consumption[J].Management of Environmental Quality,2011,4(22):440-450.

[6] 蓝伯雄，张跃.一种新型的末端物流配送服务模式[J].管理世界，2003(6):147-148.

[7] 郎茂祥.基于遗传算法的物流配送路径优化问题的研究[J].中国公路学报，2002(3):76-79.

[8] 宋少忠，孔繁森.时变路网下VRP准时路径的选择[J].吉林大学学报 （理学版），2012,3(50):309-314.

[9] 洪联系.带时间窗口动态车辆路径规划模型及其求解算法[J].计算机工程与应用，2012,48(4):244-248.

[10] 周长峰，谭跃进，廖良才.实时条件下多车辆路径与调度[J].系统工程，2006,5(24):35-39.

[11] 刘勇，崔丙谋，王小东.物流配送路径优化问题的模型及改进混合算法[J].物流科技，2008(4):26-30.