基于可重生遗传算法的大规模订单调度问题研究

0 前 言

本文研究的某风机企业属于多品种、小批量订单型生产企业，产品特点为品种多、更新快、加工产量变化大、交货周期短、工艺复杂、需求变动频繁；在此种背景下计划与调度要具有敏捷性，能够解决作业计划与调度的动态变更问题，适应企业动态生产调度的需求，使企业适应日益不确定的市场环境。

Job—Shop调度问题是NP问题，其研究的方向有两大类：精确算法和近似算法。精确算法主要包括分支定界法、基于析取图模型的枚举方法、混合整数规划模型和拉格朗日松弛法等。近似算法包括优先权规则调度算法、瓶颈转移启发式算法、邻域搜索算法和人工智能方法等。精确算法虽能保证得到全局最优解，但只能解决小规模的调度问题，无法实际应用。近年来，用邻域搜索算法，如模拟退火算法、禁忌搜索算法和遗传算法等解决Job—Shop调度问题，亦倍受关注。

当前研究较多的应用改进的遗传算法应用于生产调度，如洪刘兵、杨艳丽[1]引入人工免疫机制克隆选择算子和设计独特的交叉算子，提高算法的收敛速度和种群的多样性；曾益[2]采用的遗传算法和模拟退火算法相结合使算法能够趋于全局最优，张超勇、饶运清[3]等为克服传统遗传算法在求解车间作业调度问题时的早熟收敛，设计了一种子代交替模式的交叉方式遗传算法，传统遗传算法具有全局搜索能力，但易早熟收敛，而局部搜索善于微调，但常陷于局部最优。

为了提高种群的多样性，使其不被局部优解限制，本文运用可重生思想对遗传算法进行改进，在针对实际生产中订单调度问题调度规模大、调度复杂及计算时间长等问题，并结合企业实际建立了以最大流程时间最少为目标的订单调度模型予以优化。从而提高全局搜索能力，避免早熟。

1 问题描述及模型建立

一般的调度模型并不能应用于MTO生产中，与一般静态车间调度相比较，车间调度有如下特点： （1）产品的交付都是以订单为基本单位； （2）订单中产品种类多且数量不定，假设生产中共有μ个订单，包含m种型号的产品，且每种型号产品数量为Nm，一般生产中μ,m,Nm＞1。模型假设： （1）产品的生产工艺具有唯一性。 （2）加工过程中不能中断工序。 （3）零时刻订单中所有工件都能开始加工。根据其特点和模型假设建立如下数学模型：

目标函数：

2 模型求解

2.1 标准遗传算法

遗传算法[4]是一类借鉴生物界自然选择和自然遗传机制的随机搜索算法，非常适用于处理传统搜索方法难以解决的复杂和非线性优化问题。在遗传算法中，染色体对应的数据或数组通常用串结构数据来表示，遗传算法处理的染色体成为基因型个体，一定数量的个体组成群体。各个个体对于环境的适应程度叫适应度。其主要内容[5]包括：编码方案、适应度函数、选择策略、遗传算子等，其中交叉及变异概率分别为Pc和Pm。

2.2 可重生遗传算法

对于大规模订单调度问题，由于订单数量大及加工工艺复杂等原因，会导致运算过程中涉及数据量大，过程复杂，稳定性差，容易陷入早熟。为了提高种群的多样性，使其不被局部优解限制，本文根据文献[6]运用可重生思想对遗传算法进行改进。

（1）初始化种群大小和参数，设定种群数量为300，设置参数Pc=0.5， Pm=1。

（2）设定一个阈值ε。

（3）根据适应值函数计算各条染色体的适应值，求出每条染色体的历史最优值pbest以及历史最优值的平均值，种群在本次搜索中的最优值 gbest。

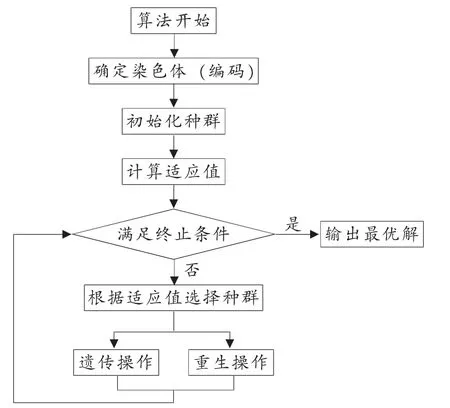
图1 重生遗传算法流程图

（4）将本次搜索中比历史最优平均值小的适应值视为适应值较小值个体，若本次搜索中的最优值gbest与适应值较小者之间的距离小于阈值ε，则适应值较小者无需重新生成，否则，将适应值较小者重新生成；除需重生的染色体外，其他染色体则进行遗传操作。

（5）判断是否满足终止条件，若满足则停止迭代输出最优解，否则转入步骤 （3）。

2.2.1 染色体编码

在遗传算法中，编码方式的设计是其关键问题，它决定了设计算法的求解精度及困难程度，必须考虑到 “个体”的可行性、有效性、合法性等，因此，应用遗传算法求解调度问题的关键就是设计遗传算法编码方式。

由于本文研究订单生产调度的特殊性，不同于一般的车间调度问题，不仅要满足一般调度问题的解码过程，而且需要考虑任何柔性设备的可交换加工特性，所以本文根据实际提出一种新的编码方案。该编码方案分为两部分，总长度为， 第一部分长度为采用依据操作的编码方式，主要是得到工件调度的先后顺序方案；第二部分长度同样为采用基于机器的编码方式，得到每个操作所在的加工设备。其中n为当前所有订单的工件数量，Ni为第i个工件所包含的操作数量。例如图2所示为一条调度3个工件的染色体，第一部分中出现的3个 “1”代表工件1的3道工序，工件2、3也同样如此；第二部分代表设备，第1个工件的第1道工序在设备1上加工，其第2道工序在设备3上加工，以此类推。

2.2.2 初始种群的产生及适应度函数

（1）初始种群的产生

图2 染色体编码方案实例

遗传算法需要初始种群数据作为搜索起点，初始种群的产生不仅要符合编码的合法性，而且关系着算法的计算效率等性能，本文根据种群编码组成的特殊性，种群产生过程也分为两个过程，首先，随机生成第一部分的编码，然后对根据工艺所要求设备的需要，再从可加工该道工序的候选设备中随机选取某台设备编号作为相对应第二部分的编码。通过此方法产生的染色体能确保染色体的合法性，提高种群生成效率。

（2）适应度函数及选择

本文选择以调度模型目标订单拖期和最小为适应度函数，即fit（）F =1/f。

选择操作采用蒙特卡罗法 （Monte Carlo），在该方法中，各个个体被选择的概率和其适应度值成比例。设种群规模大小为N，个体i的适应度值为fi，则这个个体被选择的概率为：

2.2.3 遗传算法的交叉和变异操作

（1）交叉操作：本文中交叉操作采用基于位置的交叉，而且只对染色体的第一部分进行，第二部分随着与其相应的第一部分的交叉而交叉。首先随机选取位置，然后交换被选中的基因，并在原父代个体中删除从另一父代个体交换过来的基因，接着从第一个基因位依次在未选中位置填入剩余基因。具体实例如图3所示。

图3 基于位置的交叉操作

（2）变异操作：由于调度中存在大量的工序都可在多台机器上加工，所以变异操作仅对于染色体的第二部分进行，即对某个工件的某道工序所加工的设备随机更新。

3 实例验证及数值分析

为了验证模型的有效性，本文以某订单企业为例，利用Visual Studio 2010软件，在处理器为Intel Core i3@2.27GHz@2.27GHz，内存为2GB的计算机上求解。遗传算法参数选择：种群500，交叉率为1，变异率为0.2。实验数据包括以下参数： （1）企业产品种类及在机器上的加工时间； （2）各个种类产品的加工工艺顺序； （3）某时间段具体的订单列表；数据见表1、表2、表3。

表1 调度问题的加工时间表/min

表2 调度问题加工顺序表

根据表1、表2、表3的数据分别采用标准遗传算法和基于可重生遗传算法进行10次计算 （停止标准：成熟代数达到200代），得到以下数据结果 （见表4）。

3.1 不同算法对比寻优过程

智能算法的寻优收敛过程如图4所示。从图4中可以看出，在同样的迭代数下，遗传算法比粒子群算法初始解及最终的适应值方面都要好，与标准遗传算法相比，在解已经基本稳定的情况下，即迭代340代之后，可重生遗传算法能利用其重生机制跳出原有循环，不断更新，获得更优的解。

3.2 不同订单规模下试验分析

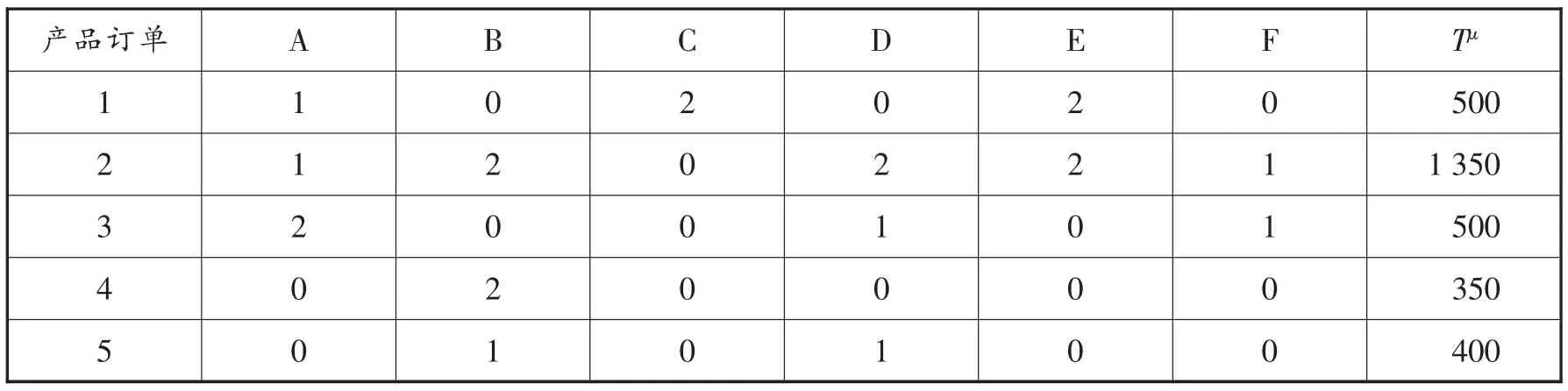
表3 某风机企业实际订单 （订单包含产品数）

表4 算法求解对比

如表5显示在不同规模下分别标准遗传算法、标准粒子群算法及可重生遗传算法所得到的计算时间及订单完成率的情况。在计算时间方面，随着产品规模的增大，标准遗传算法和可重生遗传算法相差不多，但都比标准遗传算法用时短。而订单完成率方面，在产品规模较小的情况下，三种算法都可以得到很高的订单完成率，随着产品规模的增大，可重生遗传算法明显比另外两种算法的结果更好。

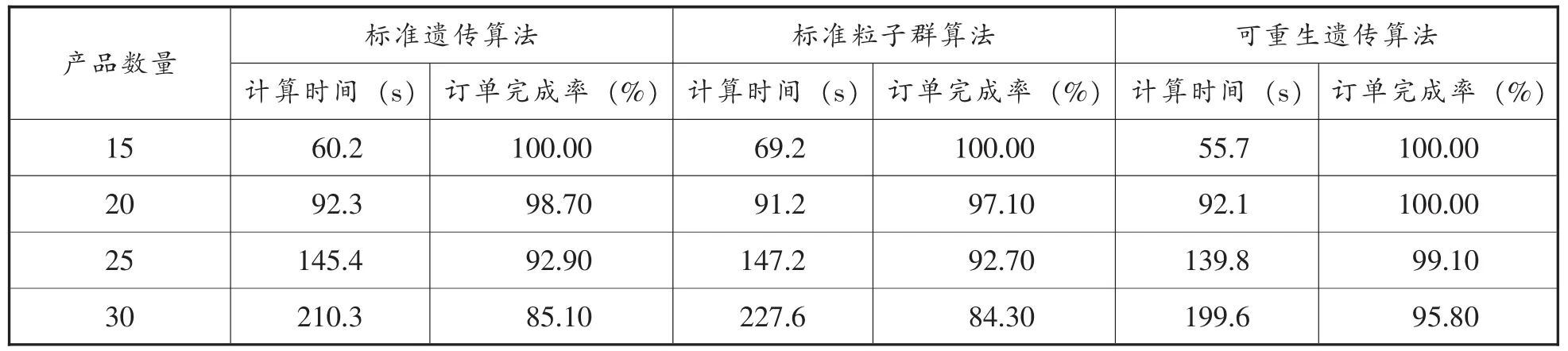
表5 不同订单产品规模下的试验结果

此实验也直接说明了可重生遗传算法在处理大规模订单调度方面比一般智能算法具有更好的效果。

4 总 结

本文根据实际建立了订单生产调度模型，针对遗传算法在计算过程中的早熟问题，基于种群可重生思想，提出了可重生遗传算法。通过与标准遗传算法及粒子群算法进行对比表明，可重生遗传算法在该问题上具有更好地调度效果，且随着订单规模的增大其调度效果方面的优势更加明显。

[1] 洪刘兵，杨艳丽.求解车间调度问题的一种改进遗传算法[J].机床与液压，2010,38(5):101-103.

[2] 曾益.一种基于改进遗传算法的车间调度问题研究[J].机械设计与制造，2011(7):180-182.

[3] 张超勇，饶运清，李培根,等.柔性作业车间调度问题的两级遗传算法[J].机械工程学报，2007,43(4):119-124.

[4] 王万良.生产调度智能算法及其应用[M].上海：科学出版社，2007:44-58.

[5] Zhenyuan Jia,Xiaohong Lu.Research on job-shop scheduling problem based on genetic algorithm[J].International Journal of Production Research,2011,49(12):3585-3604.

[6] 张捷，封俊红.基于动态距离阈值和重生机制的动态微粒群优化[J].计算机应用研究，2009,26(12):4526-4529.