立式玻璃磨边机砂轮离心振动特性分析

徐宏海，李晓阳

(1.北京工业大学 机械工程与应用电子技术学院，北京 100124;2.北方工业大学 机电工程学院，北京 100144)

立式玻璃磨边机砂轮离心振动特性分析

徐宏海1，2，李晓阳1

(1.北京工业大学 机械工程与应用电子技术学院，北京 100124;2.北方工业大学 机电工程学院，北京 100144)

针对立式玻璃磨边机砂轮架的结构特点，建立其动力学模型及系统运动微分方程，导出砂轮离心力作用下砂轮架与砂轮振动的稳态响应幅值及其动力放大因子β1、β2的理论计算公式，着重分析砂轮离心力激振下砂轮架及砂轮的振动特性及规律，结果表明：β1、β2的大小和砂轮与砂轮架的质量之比μ、固有频率之比α，砂轮角频率与固有频率之比λ，阻尼比ξ等因素有关;合理选择μ、α、ξ值，可使砂轮与砂轮架具有相同且较小的动力放大因子;避免砂轮工作在λ=0.9～1.1对应的转速范围内，可有效减轻砂轮架及砂轮的振动程度。研究结果突破了现有研究将砂轮轴刚性化处理、试验测试装备复杂等缺陷，具有物理概念清晰、计算简单等特点。

振动分析;砂轮;玻璃磨边机;离心振动

目前我国建筑能耗占能源消费总量的27.45%，其中一半通过被誉为“热洞”的玻璃门窗散失。中空玻璃是一种性价比较高的建筑节能材料，在建筑行业尤其是在中国，具有广阔的市场前景［1－5］。

玻璃磨边是中空玻璃生产过程中的一个重要环节，其功能是给平板玻璃边缘倒45°棱角，消除原片玻璃切割后玻璃边缘存在的微观裂纹和应力集中等影响产品质量的潜在缺陷，同时可避免对后续工序操作人员及设备造成伤害［6－7］。金刚石砂轮磨削是当前平板玻璃磨边的主要工艺方法，为适应大尺寸玻璃的磨边要求，磨边机多为立式结构，占地面积小［8－9］。目前国内立式玻璃磨边机市场被国外公司垄断。

玻璃磨边过程中，砂轮高速旋转产生的离心力会激励系统产生振动，从而影响玻璃磨边质量。研究砂轮及砂轮架的离心振动特性及其规律，对玻璃磨边机结构设计及国产化、提高磨边质量，具有重要的指导意义。

国内外关于立式玻璃磨边机砂轮架动力学模型与振动特性研究的相关文献报道较少，其研究方法概括起来有二种：① 试验测试与理论计算相结合方法。该方法先通过试验方法测试滚珠丝杠－螺母、丝杠轴承及直线导轨－滑块等结合面的刚度、阻尼参数，然后再用ANSYS软件进行模态分析或谐响应分析［10－11］。②理论计算法。该方法将砂轮架作为一个整体简化为单自由度系统，通过对系统运动微分方程解的分析，研究砂轮振动问题及其对加工质量的影响［12－13］。然而，上述研究存在两方面问题：① 试验测试需要搭建较为复杂的试验装备(包括样机)，且依赖于大型商用软件;②砂轮架单自由度模型将砂轮轴刚性处理，不能很好地描述砂轮与砂轮架的动态特性及其相互关系。

1 立式玻璃磨边机的工作原理

立式玻璃磨边机通常采用双砂轮架结构，如图1所示。上、下砂轮架分别采用滚珠丝杠驱动，带动上、下砂轮架在直线导轨上移动，其中砂轮1磨削玻璃的三条边，砂轮2只磨削玻璃的下边。上砂轮架驱动丝杠较长(4 m)，以适应大尺寸玻璃的磨边要求。磨边机的工作原理如图2所示：① 砂轮1自下而上磨削玻璃的右立边;② 砂轮1、2分别调整至玻璃上、下边，夹送辊带动玻璃以速度v向右移动，同时磨削玻璃的上、下边;③ 夹送辊夹住玻璃，砂轮1自上而下磨削玻璃的左立边。

图1 立式磨边机结构Fig.1 The structure of vertical glass edge grinding machine

图2 磨边机工作原理Fig.2 The principle of glass edge grinding machine

2 砂轮架动力学建模

如图3所示，砂轮架主要由框架、转筒、滚珠丝杠副、直线导轨与砂轮等组成。直线导轨固定在高刚度导轨支撑架上，滚珠丝杠驱动框架从而带动砂轮沿直线导轨作升降运动。砂轮架的动力学模型如图4所示，其中m1为砂轮架质量，m2为砂轮质量，k1为滚珠丝杠轴向综合刚度，k2为砂轮轴径向综合刚度，c为砂轮架升降运动阻尼系数，F0为砂轮不平衡离心激振力，ω为砂轮角速度。

图3 砂轮架结构Fig.3 The structure of grinding wheel carriage

图4 砂轮架动力学模型Fig.4 Dynamic model of grinding wheel carriage

该模型与阻尼减振器的动力学模型有所不同(阻尼和激振力的位置不同)，因此不能直接应用阻尼减振器振动微分方程解的计算公式。以m1、m2静平衡位置为坐标原点，系统运动微分方程如下：

在砂轮不平衡离心力F0的作用下，系统受迫振动的稳态响应为与ω相同频率的周期性振动，令x1=A1eiωt，x2=，A1、A2分别为砂轮架、砂轮受迫振动的振幅，则：

式中：λ为激励频率与砂轮固有频率之比，λ=ω/ωn2;ωn1为砂轮架固有频率，ωn1=(k1/m1)1/2;ωn2为砂轮固有频率，ωn2=(k2/m2)1/2;μ为砂轮与砂轮架质量之比，μ=m2/m1;α为砂轮与砂轮架固有频率之比，α=ωn2/ωn1;ξ为阻尼比，ξ=c/(2m1ωn1)。

3 振动特性分析

利用式(8)可以分析各种参数对砂轮架、砂轮振动的影响特性及规律，从而为玻璃磨边机设计提供重要参考依据。图5、图6为阻尼比 ξ=0、0.3、0.6时的 β1－λ、β2－λ曲线，图7、图8为砂轮与砂轮架质量之比μ=1/50、1/100、1/200 时的 β1－ λ、β2－ λ 曲线，图 9、图10为砂轮与砂轮架固有频率之比α=1、2、3时的β1－λ、β2－λ 曲线。

3.1 无阻尼振动特性分析

图5 不同阻尼情况下的β1－λ曲线Fig.5 β1 － λ curve in different damping ratio ξ

图6 不同阻尼情况下的β2－λ曲线Fig.6 β2 － λ curve in different damping ratio ξ

图7 不同质量比情况下的β1－λ曲线Fig.7 β1 － λ curve in different mass ratio μ

图8 不同质量比情况下的β2－λ曲线Fig.8 β2 － λ curve in different mass ratio μ

图9 不同固有频率比情况下的β1－λ曲线Fig.9 β1 － λ curve in different natural frequency ratio α

图10 不同固有频率比情况下的β2－λ曲线Fig.10 β2 － λ curve in different natural frequency ratio α

3.2 有阻尼振动特性分析

当 ξ≠0时，β1、β2在 λ =1时存在峰值。由式(8)可知，当 λ =1 时，β1、β2分别为

(1)β1的大小与 α2μ 成反比关系，其中 α 对 β1的影响比μ大。

(2)β2的大小与阻尼比ξ、固有频率之比α、质量之比μ等因素有关，β2随μ、α值的增大而减小(由图8、图10可知μ值对β2的影响比α大);β2随ξ的增大而增大，当ξ=∞时，系统演变为质量m2、刚度k2的无阻尼单自由度系统，β2=∞(λ=1时)。

(3)由图9、图10可知，α对β1的影响比α对β2的影响大。

(4)通过选择合适的μ、α、ξ值，可使砂轮与砂轮架在λ=1时具有相同且较小的动力放大因子，令β1=β2，由式(11)可得

另外，由图5－图10可知：当λ≤0.9或λ≥1.1时，β1、β2的值较小。

4 应用实例

本文作者课题组于2009年开发了第一代立式玻璃磨边机，其参数为：μ=1/100，α=1，ξ=0.7。该设备在使用过程中振动较大，而且玻璃边缘经常发生爆边现象。由式(11)可得β1=100，β2=140，砂轮架与砂轮振动较大。

为提高磨边质量，研制第二代立式玻璃磨边机时，对砂轮架作了轻量化设计，采用高强度铝合金材质以减轻砂轮架质量，增大μ值;同时通过结构改进增大α，改进后的参数为：μ=1/35，α=1.3，由式(12)确定阻尼比 ξ=0.3。根据式(11)计算得 β1= β2=20.7，β1和β2比第一代磨边机分别减小了79.3%和85.2%。修正设计前、后砂轮架振动加速度实测幅频曲线分别如图11、图12所示，图中60 Hz为受迫振动频率(即砂轮旋转频率)，其振幅由原来的826.3减小到286.9，减小了65.3%，与理论计算结果吻合。

图11 修正设计前振动实测幅频曲线(×100)Fig.11 Amplitude tested before improvement(×100)

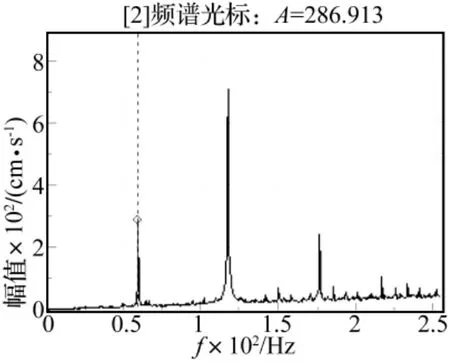
图12 修正设计后振动实测幅频曲线(×100)Fig.12 Amplitude tested after improvement(×100)

我国建筑用安全玻璃第2部分：钢化玻璃GB15763.2－2005规定：每片玻璃每米边长上允许有长度不超过10 mm，自玻璃边部向玻璃板表面延伸深度不超过2 mm，自板面向玻璃厚度延伸深度不超过玻璃厚度1/3的爆边个数1个。据生产统计，第一代立式玻璃磨边机加工的玻璃，超过国家标准规定的爆边个数最多时达3～4个，而经过修正设计的第二代立式玻璃磨边机，经一年的生产实践考验，运行正常，至今未发生玻璃爆边现象。

5 结论

(1)立式玻璃磨边机在砂轮离心力作用下，砂轮架及砂轮的振动特性和砂轮与砂轮架质量之比μ、砂轮与砂轮架固有频率之比α、激振力频率与砂轮固有频率之比λ、阻尼比ξ等因素有关。

(2)无阻尼情况下，砂轮架及砂轮在λ1、λ2处有2个共振频率，且振幅为无穷大。

(3)有阻尼情况下，砂轮架及砂轮在λ=1时发生共振，砂轮架的振幅(β1)与α2μ成反比关系;砂轮的振幅(β2)随μ、α值的增大而减小，随ξ的增大而增大。

(4)磨边机设计时，首先应尽可能减轻砂轮架的质量(增大μ值)，然后根据式(12)确定尽可能大的α并计算阻尼比ξ，这样可使砂轮架与砂轮具有相同且较小的振幅，从而提高磨边质量。

(5)玻璃磨边机在使用过程中，应避免砂轮工作在λ=0.9～1.1对应的转速范围内，可有效减轻砂轮架及砂轮的振动程度。

［1］罗宏杰.智能无机温控材料的关键基础问题［R］.上海：东方科技论坛128期，2009.

［2］闫雷光.建筑外门窗节能技术［J］.住宅产业，2009，8：62－64.YAN Lei－guang.Energy saving technology of doors and windows in architecture［J］.Housing Industry，2009，8：62 － 64.

［3］邱永忠.中空玻璃在建筑节能中的应用［J］.上海建材，2009，2：15－17.QIU Yong－zhong.Application of insulating glass in energy saving architecture［J］.Shanghai Building Materials，2009，2：15－17.

［4］Manz H.On minimizing heat transport in architectural glazing［J］.Renewable Energy，2008，33：119 －128.

［5］Yang Z，Li X H，Hu Y F.Study on solar radiation and energy efficiency of building glass system［J］.Applied Thermal Engineering，2006，26：956－961.

［6］Kondrashov V I.Shitova L A，Litvinov V A.Characteristics of cutting parameters and their effect on the glass edge quality［J］.Glass and Ceramics，2001，58：303 －305.

［7］ Popov A V.Calculation of contact pressure in cutting sheet glass with a hard－alloy metal roller［J］.Steklo i Keramika，2001，7：6－7.

［8］高文生，崔建志，贺献宝.平板玻璃磨边工艺探讨［C］//第十一届中国科协年会会议论文集，重庆，2009：1－6.

［9］Popov A V.Increasing the efficiency of diamond edging of flat glass［J］.Steklo i Keramika，2009，6：16 － 17.

［10］孔德帅，罗学科，徐宏海.立式磨边机磨头机构的动态性能分析［J］.机电工程，2011，7：802－805.

KONG De－shuai，LUO Xue－ke， XU Hong－hai.Dynamic characteristic analysis of grinding equipment in vertical ceramic edging machine［J］.Journal of Mechanical ＆Electrical Engineering，2011，7：802－805.

［11］徐宏海，李晓阳.大型立式玻璃磨边机砂轮架模态分析［J］.机械制造，2011，9：51－53.

XU Hong－hai，LI Xiao－yang.Mode analysis of grinding wheel carriage in large scale vertical glass edging machine［J］.Machinery，2011，9：51－53.

［12］赵慧丽，朱彦军.超长数控滚珠丝杠磨床砂轮振动分析及防治措施［J］.机械设计与制造，2010，3：178－179.

ZHAO Hui－li，ZHU Yan－jun.Analysis and prophylacticotherapeutic measures to the vibration of numerical control leading screw grinding machine［J］.Machinery Design ＆Manufacture，2010，3：178－179.

［13］姜永武，周 丽.砂轮不平衡量对磨削表面质量的影响［J］.制造技术与机床，2000，5：38－39.

JIANG Yong－wu，ZHOU Li.The influence of equilibrium amount ofgrinding wheelon grinding surface［J］.Manufacturing Technology ＆ Machine Tool，2000，5：38－39.

［14］诸德超，邢誉峰.工程振动基础［M］.北京：北京航空航天大学出版社，2004.

Analysis on grinding wheel centrifugal vibration behavior of vertical glass edge grinding machine

XU Hong－hai1，2，LI Xiao－yang1
(1.Beijing University of Technology，Beijing 100124，China;2.North China University of Technology，Beijing 100144，China)

The dynamic model and movement differential equations of the system were established，according to the structural specialty of grinding wheel carriage in vertical glass edge grinding machine.Expressions for steady vibration amplitudes and dynamic amplification factors(β1，β2)of grinding wheel carriage and grinding wheel actuated by grinding wheel centrifugal force were educed.Vibration behaviors were analysed.The results indicate that β1and β2are related with the mass ratio μ，the natural frequency ratio α of grinding wheel to grinding wheel carriage，the ratio λ of grinding wheel angular frequency to natural frequency and damping ratio ξ.The grinding wheel and grinding wheel carriage will have a small and equal dynamic amplification factor if reasonably selecting μ，α and ξ values.Vibration amplitudes of grinding wheel carriage and grinding wheel will be reduced greatly when ratio λ is taken between 0.9 to 1.1.Research results not only overcome shortcomings of existent methods in which the grinding wheel shaft is considered as rigid and complex equipments are necessary to do the test，but also appear clarity in physical concept and simplification in computation.

vibration analysis;grinding wheel;glass edge grinding machine;centrifugal vibration

TH113;TQ171.6

A

北京市学术创新团队项目(PHR201007119)

2011－10－25 修改稿收到日期：2012－04－18

徐宏海 男，博士生，教授，1967年11月生