阻尼环对齿轮系统轴向振动的减振特性研究

王庆洋，曹登庆，杨军波

(1.哈尔滨工业大学 航天学院，哈尔滨 150001;2.中联重科股份有限公司，长沙 410205)

阻尼环对齿轮系统轴向振动的减振特性研究

王庆洋1，曹登庆1，杨军波2

(1.哈尔滨工业大学 航天学院，哈尔滨 150001;2.中联重科股份有限公司，长沙 410205)

分析了齿轮系统的振动机理与阻尼环减振原理。建立了齿轮—阻尼环系统的轴向振动的动力学方程组，采用谐波平衡法求解动力学方程，得到了近似解析解，并与数值解进行了比较。在此基础上，采用一组典型参数，讨论了系统的幅频特性，并探讨了齿轮—阻尼环系统减振效果与阻尼环参数的关系。

齿轮;阻尼环;谐波平衡;振动特性

齿轮传动系统是机械传动领域中最为常见的传动装置，齿轮传动具有功率范围大、传动效率高、圆周速度高、传动比精确、使用寿命长、结构尺寸小等一系列特点，广泛的应用于航空航天，船舶，机械，电子等领域。而在机械传动中噪声往往是不可忽视的，齿轮传动中的振动与噪声是许多机械设备噪声的主要来源［1－2］，如何对齿轮机构进行减振降噪处理在整个机械传动领域都有着重要的意义。

齿轮的振动在形式上分为周向振动、径向振动和轴向振动。由于齿轮的各种误差以及轮齿啮合刚度的周期性变化等会对齿轮轮齿造成激励，从而引起圆周方向的振动［3］，同时这个齿面动负荷使轴和轴承产生挠曲变形，从而引起齿轮径向方向的振动。其次，在齿面载荷作用于轴承时，由于轴的挠曲变形，轴和轴承之间的摩擦引起的轴向力在齿轮的左右两端不一致，从而引起齿轮的轴向振动。也就是说径向和轴向的振动都是以圆周方向振动作为起振因素而产生的［4］。

常用的减振降噪方法有主动设计和被动减振两大类，前者优化齿轮设计参数和提高加工精度，后者是指在设计加工好齿轮之后，采用其它方法对齿轮的振动进行控制［5］。利用阻尼环进行减振降噪就是一种行之有效的被动减振方法，它在结构装配上简单，且与主动设计方法相比较为经济，阻尼环在齿轮上的镶嵌示意图如图1。阻尼环减振的基本原理为：当齿轮发生振动时，齿轮和阻尼环之间产生相对滑动，即存在滑动摩擦力;利用滑动摩擦力的耗能原理，将齿轮振动的机械能转化为由于摩擦而产生的热能，从而减小齿轮的振动能量，对齿轮的振动实现有效的控制。总之，利用阻尼环对齿轮进行减振降噪是一种简单、经济、效果显著的方法。

图1 阻尼环在齿轮上的镶嵌Fig.1 Damping ring in the gear body

于英华等［6］建立了齿轮—阻尼环系统的轴向振动模型，并进行了理论分析;孙涛等［7］建立了齿轮—阻尼环系统的扭转振动模型，采用数值方法研究了隔振效果与系统参数的关系。本文在文献［6］的基础上，建立了动力学方程组，并采用谐波平衡法进行解析求解，从理论角度研究了阻尼环的隔振效果。

1 齿轮—阻尼环系统的动力学模型

齿轮的振动分为周向振动、径向振动和轴向振动，三个方向的振动均是不可忽视的。本文仅对齿轮的轴向振动进行分析。文献［6］轴向振动模型，建立了齿轮—阻尼环系统的轴向振动动力学方程组。齿轮—阻尼环系统轴向振动模型如图2。

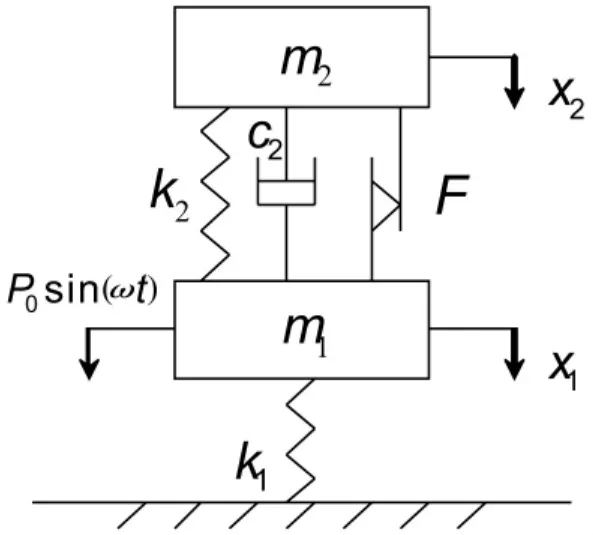
图2 齿轮—阻尼环系统轴向振动模型Fig.2 Axial vibration model of gear－damping ring

假设齿轮内部的阻尼力与由阻尼环带来的阻尼力相比小到可以忽略不计，并且将齿轮系统和阻尼环简化为集中质量。图2中m1为齿轮和轴的等效质量，即为主质量，m2为阻尼环的等效质量，k1为齿轮和轴的等效刚度，k2为阻尼环的等效刚度，c2为阻尼环的等效粘性阻尼系数，F为阻尼环与齿轮之间的滑动摩擦力。齿轮与阻尼环之间的滑动摩擦力模型采用理想的库伦摩擦模型，即滑动摩擦力的大小等于摩擦系数乘以正压力，方向与速度方向相反。图2中x1为齿轮的振动位移，x2为阻尼环的振动位移。由于齿轮在工作环境下做旋转运动，因此设其受到的外激励为简谐激振P0sin(ωt)。根据达朗贝尔原理，系统的动力学方程组如下：

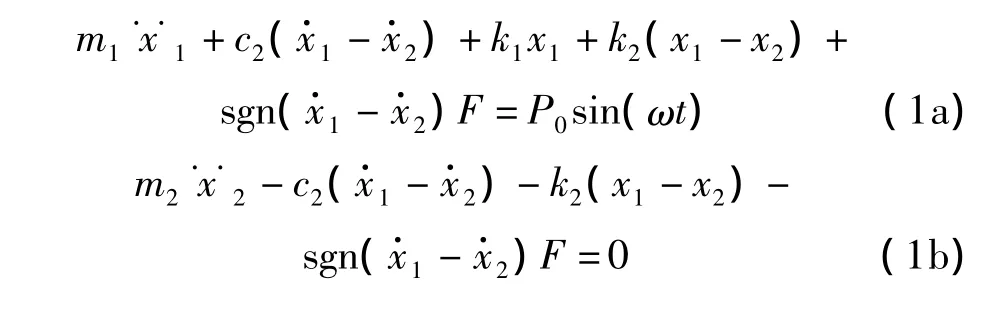
2 动力学方程的解析求解与理论分析

2.1 方程组的解析求解

式中：f是矩形波函数，如图3所示。

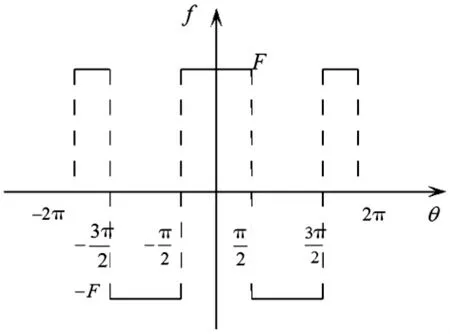
图3 滑动摩擦力f的函数图像Fig.3 Function image of the friction force f

将上述矩形波进行Fourier级数展开，即：

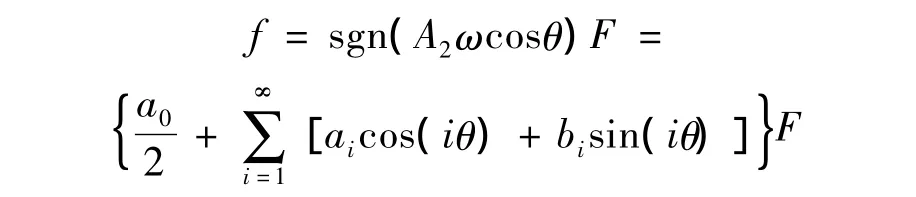
因为仅考虑系统的一次谐波响应，所以对摩擦力函数进行谐波分析时可仅考虑基波，忽略高次谐波，则有：

由于函数f是以2π为周期的偶函数，因此Fourier级数表达式中应无正弦项，即b1=0。则摩擦力函数f便可写成：

2.2 稳态周期解的存在性

3 算例分析

3.1 给定某一特定激励下的稳态响应计算

取定系统参数如下 m1=1 kg，m2=0.1 kg，k1=8 000 N/m，k2=800 N/m，c2=0.5 Ns/m，P0=30 N，激振角频率ω=70 rad/s(系统的无阻尼固有频率是ω1=76.4 rad/s，ω2=104.7 rad/s)，

阻尼环和齿轮之间的滑动摩擦力取如下四种情况，F0=0 N，F1=1 N，F2=2 N，F3=3 N，分别计算主质量的稳态响应幅值A1，其中解析解由公式(8)求得，数值解则利用Matlab直接对动力学方程(1)进行求解得到(初始位移和初始速度均取0)，并计算了相对误差，结果列于表1。

表1 不同摩擦力下的稳态响应解及误差Tab.1 Steady-state response and error under different friction force

从表1中可以看出随着滑动摩擦力的增大，解析解的误差逐渐增大，这说明了非线性项越大，解析解的误差越大。但当摩擦力为 F3=3 N时，误差为2.668%，仍在可以接受的范围之内，这也验证了利用谐波平衡法求解动力学方程(1)具有足够的精确性，即采用谐波平衡法求解是合理的。

对于利用谐波平衡法得到的解析解和用Matlab求解的数值解的图像见图4，其中滑动摩擦力取F1=1 N。从图中可以看出，数值解分为两部分，前3 s为瞬态解，3 s之后进入稳态解阶段。

3.2 幅频特性分析

取定系统参数如下 m1=1 kg，m2=0.1 kg，k1=8 000 N/m，k2=800 N/m，c2=0.5 Ns/m，P0=30 N(系统的无阻尼固有频率是 ω1=76.4 rad/s，ω2=104.7 rad/s)。选取滑动摩擦力四种情况：F0=0 N，F1=1 N，F2=2 N，F3=3 N。

利用式(8)绘制的幅频特性曲线如图5。从图5中可以看出，随着滑动摩擦力的增大，在共振处的响应峰值依次减小，说明滑动摩擦力的作用确实有助于减振降噪。齿轮与阻尼环之间的滑动摩擦力的大小取决于二者间的材料摩擦系数和正压力的大小，而正压力的大小取决于阻尼环的压缩量。总之，可以从选用阻尼环的材料以及压缩量来对阻尼环进行设计，以便于实现更好的减振效果。

对于上述讨论中的数据参数仅将阻尼改为c2=3 Ns/m，其它参数不变。仍选取滑动摩擦力四种情况：F0=0 N，F1=1 N，F2=2 N，F3=3 N，利用式(8)绘制幅频特性曲线如图6。

将图6与图5比较可知改用大阻尼后，振动响应的最大幅值显著下降，而且第二阶固有频率对应的峰值由于过小，已经从图中显现不出来。从而可以得出利用高阻尼材料制作阻尼环可以得到较好的减振效果的结论。图6还可以看出随着干摩擦力的增大，振动响应的最大幅值并不是一直减小，当超过某一临界值后，干摩擦力增大，振动响应的最大幅值反而上升。也就是说并非是干摩擦力越大，减振效果越好，即存在一个最佳摩擦力，使减振效果最好，当齿轮、阻尼环材料选定时，最佳摩擦力与正压力有关，因此在设计阻尼环时压缩量即不能过大，也不能过小。这与文献［5，10］中讨论的内容是一致的。

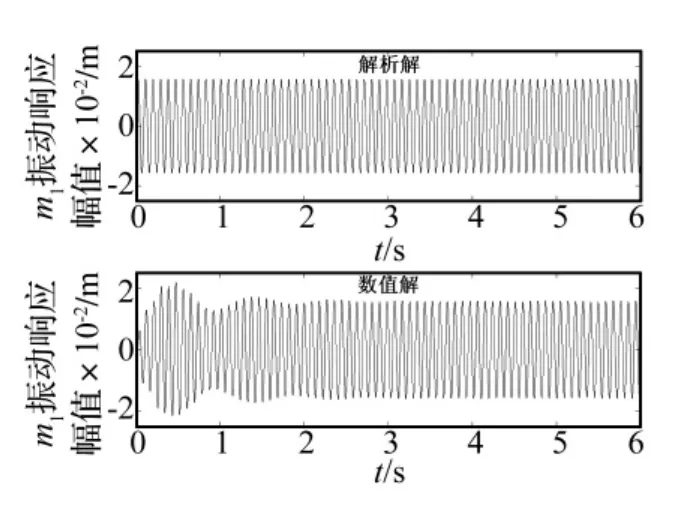
图4 两种方法求解的比较(F=1 N)Fig.4 The comparison by two kinds of solving methods

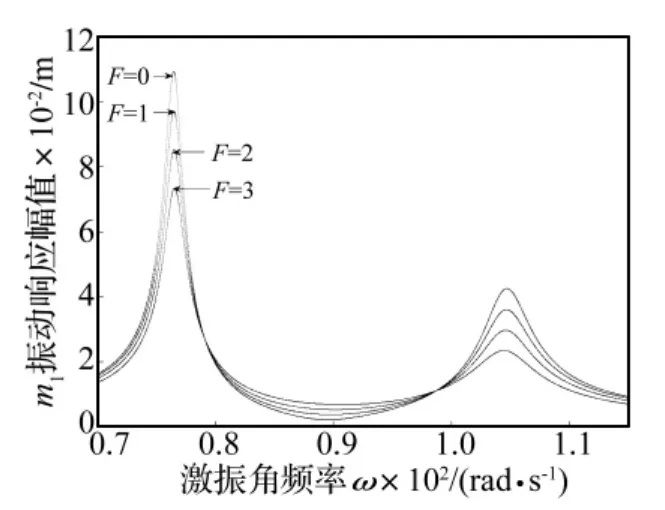
图5 幅频特性曲线(c2=0.5 Ns/m)Fig.5 Amplitude－frequency characteristic Curve(c2=0.5 Ns/m)

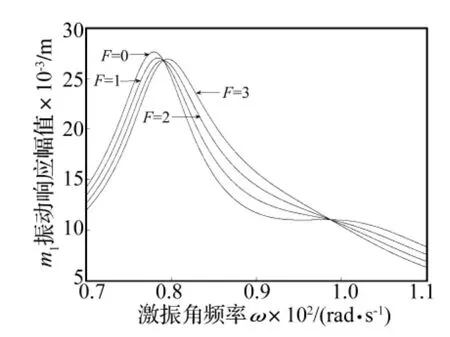
图6 幅频特性曲线(c2=3 Ns/m)Fig.6 Amplitude－frequency characteristic Curve(c2=3 Ns/m)

4 结论

利用文献［6］的假设，建立了齿轮－阻尼环系统轴向振动的动力学方程组，利用谐波平衡法，求出了动力学方程组的解析解，并将解析解与Runge－Kutta数值解进行了比较，二者相差很小，证明了解析解法的精确性与合理性。给出了系统存在稳态响应的条件。在特定的工况下，得到了系统的幅频特性曲线，讨论了系统的稳态响应最大值与阻尼和滑动摩擦力的关系，结果表明：采用高阻尼材料减振效果好;在一定滑动摩擦力范围内，增大滑动摩擦力有助于减振，但滑动摩擦力并不是越大越好，即齿轮—阻尼环系统存在最佳摩擦力的概念。

［1］Smith J D著.吴佩江译.齿轮振动与噪声［M］.北京：中国计量出版社，1989，4－5：87－88.

［2］齿轮手册编委会.齿轮手册［M］.北京：机械工业出版社，2004：3－8.

［3］李润芳，王建军.齿轮系统动力学［M］.北京：科学出版社，1997：352－355.

［4］张 展.齿轮的噪声［J］.矿山机械，1983，(2)：49－55.ZHANG Zhan. Gearnoise［J］. Ming ＆ Processing equipment，1983，(2)：49 －55.

［5］古成中，吴新跃.齿轮被动减振技术研究［J］.机械设计与制造，2010，(9)：74 －76.

GU Cheng－zhong，Wu Xin－yue.Passive vibration damping technology of gear［J］.Machinery Design ＆ Manufacture，2010，(9)：74－76.

［6］于英华，梁 冰.泡沫铝齿轮阻尼环减振降噪特性分析［J］.沈阳工业大学学报，2004，26(3)：247－249.

YU Ying－hua， LIANG Bing.Research on properties of reduction of vibration and noise with foamed aluminum damping－ring. ［J］. JournalofShenyang University of Technology，2004，26(3)：247－249.

［7］孙 涛，沈允文，刘继岩.齿轮阻尼环的最佳摩擦力分析［J］.机械传动，1999，23(2)：16－18.

SUN Tao，SHEN Yun－wen，LIU Ji－yan.Analysis of the optimal frictional force on gear damping rings［J］.Journal of Mechanical Transmission，1999，23(2)：16－18.

［8］He E，Wang H.A new multi－ harmonic method for predicting the forced response of mistuned bladed disks with dry friction damping［J］. ComputationalMethods in Engineering and Science，2006：1149－1157.

［9］白鸿柏，黄协清.干摩擦振动系统响应计算方法研究综述［J］.力学进展，2001，31(4)：527－534.

BAI Hong－bo，HUANG Xie－qing.An overview on study of methods of response computation for the dry frictionally damped vibration systems［J］.Advances In Mechanics，2011，31(4)：527－534.

［10］丁 千，谭海波.干摩擦阻尼叶片周期振动响应的解析计算［J］.机械强度，2005，27(5)：571－574.

DING Qian，TAN Hai－bo.Solving periodic response of dry friction damper blades using analytical method［J］.Journal of Mechanical Strength，2005，27(5)：571－574.

［11］白鸿柏，张培林，黄协清.干摩擦动力吸振器简谐激励响应计算的最优化方法研究［J］.振动与冲击，2000，19(3)：43－45.

BAI Hong－bo，ZHANG Pei－lin，HUANG Xie－qing.Study on response computation method of a two degrees－of－freedom vibration absorber system with variable coefficient of sliding friction using optimum approximate technique［J］.Journal of Vibration and Shock，2000，19(3)：43－45.

Axial vibration reduction characteristics of a gear system with a damping ring

WANG Qing－yang1，CAO Deng－qing1，YANG Jun－bo2

(1.The school of Astronautics，Harbin Institute of Technology，Harbin 150001，China;2.Zoomlion Heavy Industry Science＆ Technology Development Co.，Ltd.，Changsha 410205，China)

The vibration mechanism of a gear system was analyzed，and the anti－vibration principle as regards a damping ring device was elaborated.The axial vibration equations of a gear－damping ring system were established.The harmonic balance method was employed to obtain an approximate analytical solution which was used to compare with the numerical solution.On this basis，by using a set of typical data，the amplitude－frequency characteristic was discussed.The relationships between vibration reduction characteristics and the parameters of system were also discussed.

gear;damping ring;harmonic balance;vibration characteristic

TH13

A

国家自然科学基金(50935002)

2011－12－20 修改稿收到日期：2012－04－27

王庆洋 男，硕士生，1988年生

曹登庆 男，博士生导师，1958年生