参数已知下比例函数线性模型的积分估计①

常克亮， 陈贵景

(山西大同大学数学与计算机科学学院，山西 大同037009)

0 引 言

Tibshirani 和Hastie 在(1993)1 提出了变系数模型，由于“维数祸根”产生很多不便，人们在不同情况下进行了改进，参看文献［2 ～5］. 张和卢(2004)［6］对其进行改进提出了如下模型

称为比例函数线性模型. 其中Y 是响应变量，X =(X1，X2，…，Xp)T和Z = (Z1，Z2，…，Zp)T是为解释变量，X 与Z 可能相互独立也可能不相互独立;ε 独立于X 和Z，且E(ε)= 0，Var(ε)= 1;σ(·，·)是从R2p到R 的一个已知可测函数;g(·)是从R 到R的一个未知可测函数;Cα(γ)，(α = 1，…，p)是参数γ 的已知函数，γ = (γ1，γ2，…，γp)T的可知性不确定，我们来考虑在假设γ 已知的条件下，讨论系数函数积分估计及其渐近正态性，我们记Cα=Cα(γ)(α = 1，…p).

1 估计和渐近正态性

设{Yi，Xi，Zi，i = 1，…，n}是从模型(1)中取得的简单随机样本，其中X1= (Xi1，Xi2，…，Xip)T，Zi= (Zi1，Zi2，…，Zip)T.假设g(·)的二阶导数保持Lipschitz 连续性，可知在g(Xα)的支撑内的一点xα周围必然能用一个线性函数来逼近，即:，其中，aα= g(xα)，bα= hαg'(xα).

对下式

关于{aα，α = 1，…，p}和{bα，α = 1，…，p}极小化，设(x)是使(2)式达到极小化的解的前p 个值，由最小二乘思想，可得

其中，x = (x1，x2，…，xp)T，eα，2p是第α 个分量为1的2p 维单位向量，U 是一个n ×2p 的矩阵，它的第i 行是

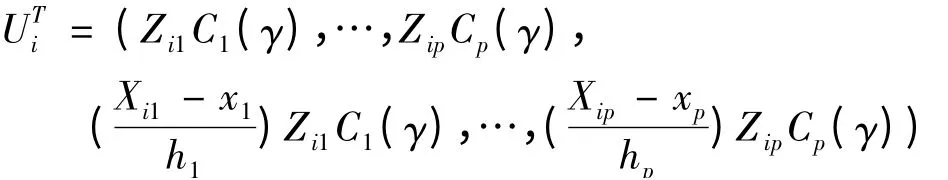
W = diag(W11，W22，…，Wpp)，它的第i 个对角线元素是Wii= Khα(Xiα-xα)，Xiα是Xα的第i 个观测值，Ziα是Zα的第i 个观测值，Khα(·)= h-1αK(·/hα)，K(·)是一个具有紧支撑而且关于0 对称并且有界非负的Lipschitz 连续的概率密度函数，hα= hnα＞0 称作窗宽.

令x-1= (x2，…，xp)T，假设Q-1(x-1)是一个权重函数，且满足∫dQ-1(x-1)= 1. 设q-1(x-1)是Q-1(x-1)的概率密度函数，而且要求Q-1(·)的支撑在X-1的取值范围内.

在(3)式的前提下，采用积分方法定义g(·)的积分估计:

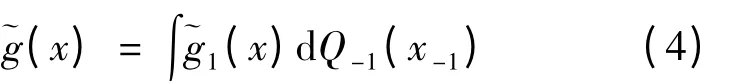
条件:

A1.X 的联合密度p(x)以及Xα的边际密度pα(xα)是存在紧支撑的，有界的，Lipschitz 连续的;

A2. 条件期望E(Zα，Zα'，σ2(X，Z)| X = x)，E(Zλα1Zλα2σ2(X，Z)| X = x)是Lipschitz 连续的，其中:λ1+λ2= 2 或4，λ1≥0，λ2≥0，α，α' = 1，…，p.

定理: 假设A1 和A2 都成立，窗宽满足hα→且h1= Bn-1/5，nh5α'→0，α' = 2，…，p，B 是一个常数，有

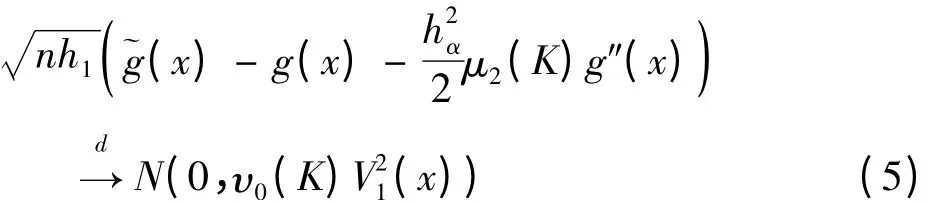
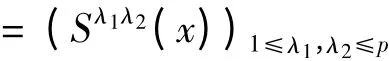
C = diag(C1，C2，…，Cp)，p-1(x-1)是x-1= (x2，…，xp)的边际密度.

证明: (参考文献5).

2 结 论

用积分方法得到系数函数的积分估计，并且讨论了估计的渐进正太性.

［1］ Hastie，T. andTibshirani，R. Varying - coefficient models［J］.Statist.Soc.B，1993，55(4):757 -796.

［2］ Cai，Z.，Fan，J. Avreage regression surface for dependent［J］.Multivaraiate Anal，2000，75:112 -142.

［3］ Cai，Z.，Fan，J，Yao，Q. Function-coefficient models for nonlinear time series［J］.American Statist，Assoc. 2000.95(451).

［4］ Fan，J，Zhang，J.Two-step estimation of functional lineat models with applications to longitudinal data［J］.R.Statist，2000，B62，303 -322.

［5］ Zhang，R.Q.andLi，G.Y. Avreage estimation of Function-coefficient regression models with different smoothing variables［J］.Statistics ＆ Probability，2007，77:455 -461.

［6］ 张日权，卢一强.变系数模型［M］.北京:科学出版社，2004.

［7］ 常克亮，陈贵景.参数已知下比例函数线性模型的平均估计［J］.佳木斯大学学报(自然科学版)，2012，30(6):917 -919.