混凝土中温度对氯离子扩散系数的影响分析①
2013-02-02刘毅
刘 毅
(1.同济大学岩土及地下工程教育部重点实验室,上海200092;2.同济大学地下建筑与工程系,上海200092)
0 引 言
近年来,许多学者建立了各种混凝土寿命预测模型,绝大部分是建立在氯离子扩散理论的基础上[1].影响氯离子在混凝土中扩散的因素很多,比如:混凝土材料、应力和裂缝、表面氯离子浓度、干湿循环等等,因此,不少学者提出了对扩散系数的修正公式[2~4].当考虑温度对氯离子扩散系数影响时,几乎所有学者都引用了Boddy[4]或N. S.Berke[5]文中采用的引入Arrhenius 公式的修正模型,并附上了文中给出的活化常数参考值[6~9].
然而,在Boddy 和N.S.Berke 的原文中并没有阐明两个公式的确切来源,也没有给出相关参数的取值依据.如果直接引用该结论,可能会对混凝土中氯离子侵蚀程度造成误判,进而影响混凝土的寿命预测和耐久性评估.
为了合理地分析温度对混凝土中扩散系数的影响,建立更加准确的混凝土寿命预测模型,本文对此追本溯源,推导了考虑温度影响的氯离子扩散系数计算公式,肯定了引入Arrhenius 公式考虑温度作用的合理性.对相关腐蚀试验结果分析,进一步地发现混凝土活化能与掺合料的种类和数量相关.
1 固、液体中的扩散系数
1.1 液体中的扩散系数
Einstein 提出用水力摩擦型估算无限稀释浓度下溶质的扩散系数,提出著名的Einstein - Stokes方程[10]:
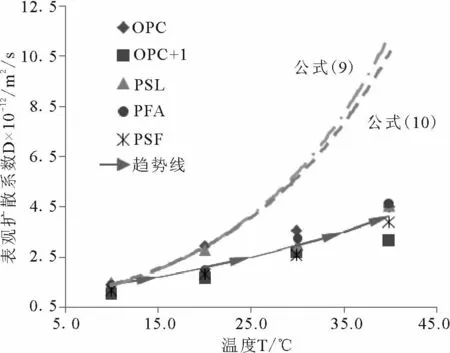
图1 扩散系数变化趋势曲线

式中,k 是玻耳兹曼常数,μ 是溶剂粘度,R0是溶质的半径,T 是温度. 该方程假设溶质粒子大小要远大于溶剂粒子大小,不适合溶质与溶剂粒子大小相似的情况,也只能限制在稀释溶液中适用. 不少研究者针对E - S 方程提出了改进,一般都认可式中温度与粘度对扩散系数的影响关系,而对其他参数进行修正[11]. 由此可以看出,对于溶液中的扩散,扩散系数D 一般正比于温度T,反比于溶剂粘度,引入常数A1,可统一采用下式表达这一关系:

Eyring 提出反应速率理论来计算液体的粘度,他认为液体分子要从空间一个位置到另一个位置必须克服一个能垒,分子必须具有较高的能量,越过能垒才能实现移动[12]. 分子越过能垒的速率类似于反应速率,即Arrhenius 公式:

结合上式、牛顿运动定律和液体结构,Eyring 得到液体粘度的表达式:
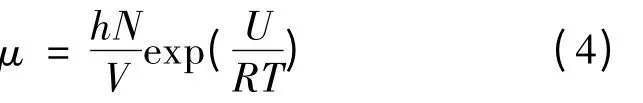
式中,k'是反应速率,A2是试验参数,N 是阿佛加德罗常数,V 是摩尔体积,h 是普朗克常数,R 是理想气体常数(8.314J/mol·K),U 是活化能(kJ/mol).根据上式,为了得到温度对扩散系数的影响,引入A3= hN/V 液体粘度可以通过下式表达:

综合式(2)和式(5)可得稀溶液中的扩散系数随温度的变化公式为:
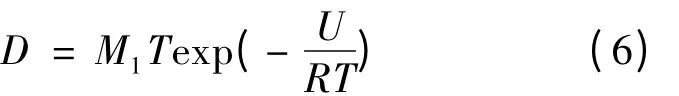
式中,M1和U 为可根据试验测出.
1.2 固体中的扩散系数
一般来说,固体中的扩散系数的计算是不准确的,需要通过试验进行测量. 如果实在要粗略估算的话,也只能依据面心立方体(FCC)金属的计算理论,计算公式如下[10]:

式中,R1是原子之间的间隔距离,n 是晶格位的空缺率;ω 是跃变频率. 跃变频率与原子振动频率和迁移活化能有关,也可以通过Arrhenius 公式表达.于是扩散系数D 的估计值可以写成:
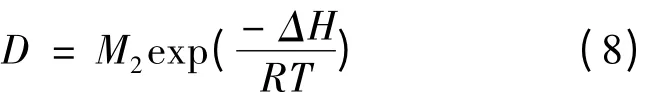
式中,M2和ΔH(kJ/mol)是试验值. 由于试验出来ΔH 值非常大,所以扩散系数随着温度的变化非常显著.
物质在纯净固体中的扩散系数一般是非常小的,比如,C 在铁素体α - Fe 中的扩散系数都小于10-20(cm2/s)的数量级.但是绝大部分现实中的固体不是纯净物,而是混合物,甚至是带有很多杂质、缺陷的混合物.物质在这样的固体中扩散时,一般会沿着内部的缺陷或“空位”迅速向内部侵入,而使测试出的扩散系数相对较大,比如,Ti4+f 和Fe2+致色离子在蓝宝石中的扩散系数就达到10-9(cm2/s)数量级[13].
2 混凝土中的扩散系数
式(6)中稀溶液中溶质的扩撒系数计算公式可以改写成如下形式:

同理,式(8)中固体中物质的扩散系数估算公式可以改写成如下形式:

式中,D0是在温度T0下测定的扩散系数(m2/s),q是被气体常数平分之后的活化能(K).
事实上,式(9)正是1994 年N.S.Berke 等用于描述不同温度对氯离子扩散影响的表达式,而式(10)正是1999 年Boddy 和2000 年Onyejekwe 等采用的方法. 另外,N.S.Berke 还给出了单位活化能的估算参考值:当w/c = 0.4 时,q = 6000K;当w/c= 0.5 时,q = 5450K;当w/c = 0.6 时,q = 3850K.
目前,国内很多学者在讨论温度对氯离子扩散影响时都是基于上述两式,采用的分析参数也是1994 年N.S.Berke 给出的参考值.
3 讨论与分析
上述两式用于计算混凝土中氯离子扩散系数时存在以下两个问题:①混凝土是一种成分复杂、结构松散、容易劣化的胶凝材料,在混凝土扩散问题中引入化学反应中平衡常数与温度的关系式——Arrhenius 公式是否合理②如果合理,那么N.S.Berke 中采用单位活化能来描述温度对扩散的影响,其提出的单位活化能参考值又是否正确.
3.1 Arrhenius 公式的合理性
首先,混凝土区别于晶体的一个重要的特征就是混凝土具有多孔性,而孔隙结构和孔隙率又与其渗透性直接相关. 从微观结构上看,混凝土的孔隙率、孔径分布以及骨料-基体界面区的矿物组成都会影响到渗透性,毛孔越大,渗透性越强.普通混凝土的界面区疏松多孔,界面区Ca(OH)2富集生长,往往成为各种有害介质侵入其内部的通道,对渗透性影响很大[14].其次,我们一般说的氯离子在混凝土中的“扩散”,是一个不准确的概念,包括了扩散、对流、电迁移等过程,其中主要的是扩散和对流.
当混凝土表面有自由氯离子存在时,氯离子或其依附的孔隙液就会通过混凝土中的毛细孔或结构空隙向混凝土内部渗透.这就需要依靠对流的两种方式——渗流作用和毛细作用.渗流作用是在外界压力的作用下孔隙液发生定向移动,毛细作用是为了到达毛细管内液面两侧压力平衡而发生液体流动的现象.两者的速率也是和溶液粘度呈负相关的[15],因而也会随着温度的升高而增加,从(4)式中看出,这是符合Arrhenius 公式的.
与此同时,由于混凝土孔隙率较小,很大部分的氯离子是通过混凝土中的砂石等骨架向内部扩散.这样的扩散方式类似于C 在Fe 或Cu 等晶体中的扩散,只是由于混凝土结构相对疏松,所以前者扩散速率要比后者大得多. 从(8)式中可以看出,固体中的扩散系数随温度的变化正是通过Arrhenius 公式表达的.
另外,工程环境温度随季节的变化一般在10~40℃,更低的温度对减缓氯离子在混凝土中的扩散是有利的,而更高的温度在大部分地区很难出现.当实际环境中的温度变化不大时,可认为温度对活化能和指前因子没有影响[16],Arrhenius 公式仍具有很高的适用性.
然而,混凝土本身属于固体材料,从扩散的角度来讲,其多孔性也类似于其他固体材料中的结构缺陷.氯离子在混凝土中的扩散相对而言更接近于固体中的扩散机理,因此采用式(10)进行计算显得更加合理.
3.2 单位活化能的取值
2004 年同济大学材料学院的施惠生教授通过试验研究了不同温度作用下不同掺合料的混凝土中氯离子的扩散系数[17].试验中的水灰比均为0.35,根据N. S. Berke 的参考值外推,近似取q =6200K,根据上述两式和试验数据绘制出的扩散系数的变化趋势如图1 所示.
从图1 中可以看出,不同混凝土中氯离子扩散系数随温度的变化趋势(图中带箭头的曲线所示)基本上是符合Arrhenius 公式的,具有随温度升高而增加且增加幅度不断增大的趋势. 但是采用N.S.Berke 给出的参考值绘出的变化曲线(图中虚线所示)却得出了很高的结果,比实测的扩散系数大了2 ~3 倍.由此可见,N.S.Berke 给出的参考值并不适合施惠生试验配制的混凝土.
表1 中给出了施惠生试验中的混凝土配制参数以及采用式(10)对试验结果拟合得到的单位活化能.从表中可以发现,在水灰比一定时,单位活化能并不是恒定的,随着掺合料的种类和数量变化较大.其中,硅粉的影响最大,其次是粉煤灰,最后是矿渣.

表1 单位活化能
由于目前相关试验非常少,难以全面确定影响混凝土单位活化能的因素,和其影响程度. 所以本文建议,在考虑温度对氯离子在混凝土中扩散的影响时,要充分考虑混凝土材料的差异性,不能盲目地引用N.S.Berke 给出的参考值.
4 结 语
本文通过推导和分析,得到了以下两点结论:
①在常温环境下,引入Arrhenius 公式描述温度对氯离子在混凝土中扩散的影响是合理的,并建议采用Boddy 给出的计算公式.
②活化能不仅与水灰比相关,也受掺合料的种类和数量影响.另外,可能还存在其他的影响因素.因此,对活化能的取值应该慎重,建议采用相关试验测试.
[1] 范宏,赵铁军,田砾. 氯离子标准扩散计算模型用于寿命预测分析[J]. 青岛理工大学学报,2006,27(2):18 -23.
[2] 余红发,孙伟,麻海燕,等. 混凝土在多重因素作用下的氯离子扩散方程[J]. 建筑材料学报. 2002,5(3):240 -247.
[3] 孟宪强,王显利,王凯英. 海洋环境混凝土中氯离子浓度预测的多系数扩散方程[J]. 武汉大学学报(工学版),2007,40(3):57 -60.
[4] Boddy A.,Bentz E.,Thomas M.D.A.,et al. An Overview and Sensitivity Study of a MultimechanisticChloride Transport Model[J]. Cement and Concrete Research,1999,29(6):827 -837.
[5] Berke N.S.,Hicks M.C.. Predicting Chloride Profiles in Concrete[J]. Corrosion Engineering,1994,50(3):234 -239.
[6] Amey S.L.,Johnson D.A.,Miltenberger M.A.,et al. Predicting the Service Life of Concrete Marine Structures :An Environmental Methodology[J]. StructualJournal,1998,95(2):205 -214.
[7] 余红发,孙伟,麻海燕,等. 混凝土使用寿命预测方法的研究Ⅲ——混凝土使用寿命的影响因素及混凝土寿命评价[J].硅酸盐学报. 2002,30(6):696 -701.
[8] 何文敏. 混凝土结构使用寿命预测模型研究综述[J]. 材料导报,2011,25(8):141 -144.
[9] 王立成. 氯盐环境下钢筋混凝土结构使用寿命评价的研究进展[J]. 水利水运工程学报,2004(4):54 -60.
[10] Cussler E L. Diffusion Mass Transfer in Fluid Systems[M].Cambridge University Press,1997:631.
[11] Poling B E,Prausnitz J M,O'Connell J P. The Properties of Gases and Liquids[M]. Fifth Edition ed. New York:McGRAWHILL,2001.
[12] Eyring H. Viscosity Plasticity and Diffusion as Examples of Absolute Reaction Rates[J]. Journal of Chemical Physics,1936,4(4):283 -291.
[13] 杨如增,程毅. 蓝宝石中Fe2+和Ti4+离子的扩散系数及其对扩散处理工艺的影响[J]. 宝石和宝石学杂志,2003,5(4):7 -10.
[14] 李淑进,赵铁军,吴科如. 混凝土渗透性与微观结构关系的研究[J]. 混凝土与水泥制品,2004,(2):6 -8.
[15] 张奕.氯离子在混凝土中的输运机理研究[D]. 杭州:浙江大学,2008.
[16] 刘云. 对Arrhenius 公式中一些问题的讨论[J]. 内江师范学院学报,1997,(4):14 -21.
[17] 施惠生,王琼. 混凝土中氯离子迁移的影响因素研究[J].建筑材料学报,2004,7(3):286 -290.
