基于融合特征降维的场景分类研究
2013-01-31付赛男邹维嘉
付赛男,朱 俊,张 瑞,邹维嘉
(上海交通大学图像通信与网络工程研究所,上海200240)
在过去的十多年中,场景分类在计算机视觉领域受到了很大的重视。所谓场景分类,就是自动判别一个语义类别集中的一幅场景图像属于哪个场景类(如海岸、山脉和街道)[1]。目前已有很多用于场景分类的方法。总体来说,场景分类共有两步:第一步,提取图像的描述子来表示图像;第二步,在第一步的基础上,通过使用分类器把输入的场景图像分为不同的场景类别。
简单地,可以提取一种图像特征来表示图像,到目前为止,应用到场景分类的图像特征有很多种,用于表示图像的特征包括纹理特征、颜色特征等。尺度不变特征转换SIFT(Scale Invariant Feature Transform)是一种在物体识别领域广泛应用的图像描述子[2],CENTRIST(Census Transform Histogram)是一种适用于场景分类的图像特征。对于不同的图像,会有很不同的视觉感受。Wu和Rehg[3]对不同的图像特征用于图像分类的结果进行了研究,发现一些图像特征对于场景分类能得到很好的分类准确率,但对物体识别却很难得到好的结果,而另外一些图像特征恰恰得到相反的结果。所以,对一组图像特征进行融合来表示图像而不是只使用一种图像特征,使用多线索的方法是目前图像分类的一个趋势。
对不同的图像特征进行融合的最简单方法就是直接把不同的几种特征向量串接成一个特征向量来表示图像。文献[4]提出了一种使用词袋模型(Bag-of-Words Model)和空间金字塔的多图像特征通道来表示的图像的框架。Varma和Ray[5]通过使用多核学习MKL(Multiple Kernel Learning)对多个不同的图像特征进行融合,并且在几个基准数据集上都得到了很好的分类结果。
1 总体架构
如果使用多线索的方法,就很有可能得到一个高维的图像特征描述子,在做实验的时候需要更多的内存空间和更长的实验时间。而且还存在另外一个不可忽视的问题,即这一组用来表示图像的特征信息是否都必要。一般来说,融合的图像描述子可能包含冗余信息或噪声等,导致不好的实验结果。
本文主要关注场景分类的第一步,即图像的表示。使用SIFT、CENTRIST、基于梯度方向直方图HOG(Histogram of Oriented Gradients)、GIST这4种图像特征进行融合得到一个特征向量来表示图像。提出了使用主成分分析PCA(Principal component Analysis)对融合的图像特征进行降维。
在上面所提到的第二步中,使用线性核的支持向量机SVM(Support Vector Machine)[6]。首先使用所选取的数据集中的训练样本训练模型,然后对数据集中的测试图像进行测试,并对得到的实验结果进行评价。
实验流程图如图1所示,分别提取了图像的4种图像特征:SIFT,CENTRIST,HOG和GIST。SIFT用来侦测与描述影像中的局部性特征,它在空间尺度中寻找极值点,并提取出其位置、尺度、旋转不变量,此算法由David Lowe在1999年发表[7],对于光线、噪声、些微视角改变的容忍度也相当高。CENTRIST通过计算图像中每个像素点的CT(Census Transform)值来得到图像的局部结构信息,而大尺度的结构信息是由相邻像素CT值的强相关性和统计各个像素CT值得到的CT直方图得到[8]。这里的GIST模型计算加窗傅里叶变换的幅度谱,选取4×4等大、无重叠的区域作为窗[9]。HOG特征是在均匀分布的密集网格上计算梯度方向的个数,并使用局部对比归一化以提高准确率。
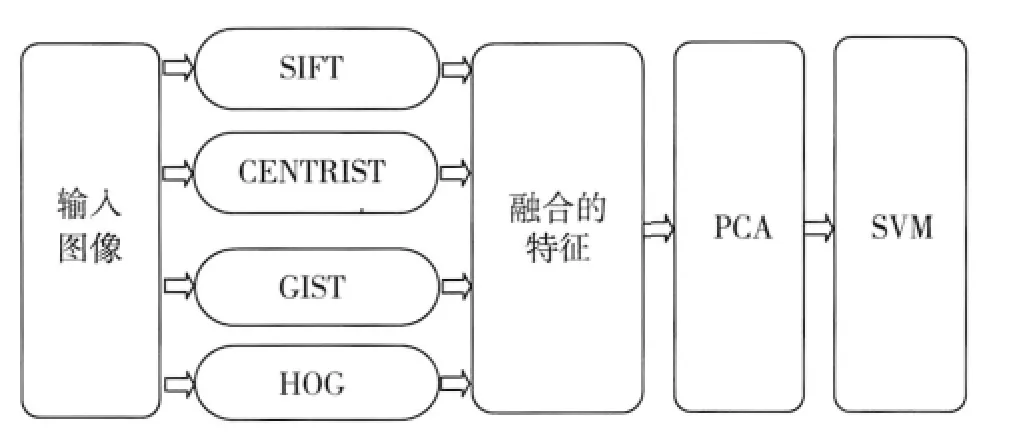
图1 实验框架
把4种图像特征直接串接到一起,得到了图像的融合特征向量。接下来,使用PCA对融合的特征向量进行降维。PCA是一种基于特征向量的、最简单的多元分析方法[10]。它可以从多元事物中解析出主要影响因素,揭示事物的本质,简化复杂的问题,计算主成分的目的是将高维数据投影到较低维空间。对已知m×k维的矩阵X(X是1个共有m个样本,特征维数为k的矩阵),首先对其进行中心化得到m×k维的矩阵X1(每列均值为0,方差为一确定值),即
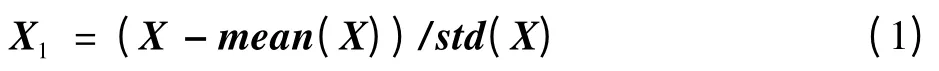
式中:mean(X)是对矩阵X的每列求平均得到的1×k维的矩阵;std(X)是对矩阵X的每列求标准差得到的1×k维的矩阵。
计算矩阵X1的协方差矩阵V

可以得到m×m维的协方差矩阵V的特征值v和特征向量D(每1列为1个特征向量)。把v和D均按特征值大小降序排列,可以得到投影矩阵,n是想要降到的维数。
最后,得到投影后的矩阵Xpro,即

使用SVM对用特征表示的图像进行训练和测试。
2 实现细节
2.1 图像预处理
提取特征之前首先对数据集做预处理,把彩色图像转换为灰度图像,SIFT、GIST这两种特征还需要把灰度图像的大小调整一致,本文中提取SIFT特征时,图像大小调整为300×300,而对于GIST特征,调整为256×256。
2.2 实验细节
本文中使用了标准的SIFT(即选取词典大小V为512,VQ编码,sum pooling以及使用3层金字塔),并结合词袋模型来表示图像。所谓词袋模型,就是通过量化视觉特征,用类似于单词的视觉特征来表示图像[11]。提取CENTRIST特征时,首先计算各个像素的CT值,然后统计CT值的直方图,即得到图像的CENTRIST特征表示。对于HOG特征,本文中使用不重叠的分块分别提取HOG特征。
在提取上述4种特征之后,要把每幅图片的每种特征都转化为1个行向量表示,把该行向量作为后面分类器的输入。在融合特征的时候,只需把1幅图像的4种特征的行向量串接一起得到1个更高维的行向量,这就是所得到的融合之后的特征。
2.3 参数设置
对于4种特征和融合特征,在加入PCA之后,有2个参数可供调整:1)想要降到的维数n;2)第二步中分类器可调参数C。
对于原始10 752维的SIFT特征,对于每次试验,分别选择了维数n=10 000,9 000,8 000,7 000,5 000,3 000,2 000,1 000,800,600,400,200,100,50和参数C=-5,-3,-1,1,3,5,7。
对于原始256维的CT特征,对于每次试验,分别选择了维数n=200,150,100,50和参数C=-5,-4,-3,-2,-1,0,1,3,5。
对于原始1 024维的HOG特征,对于每次试验,分别选择了维数n=950,800,600,400,200和参数C=-9,-7,-5,-3,-1,1。
对于原始312维的GIST特征,每次试验分别选择了维数n=300,250,200,150,100,50和参数C=-5,-3,-2,-1,1,3,5。
对于融合的特征,每次试验分别选择了维数n=12 000,11 000,10 000,9 000,8 000,7 000,5 000,4 000,3 000,2 000,1 000,700,400,200,100,50,30和参数C=-5,-3,-1,1,3,5,7。
3 实验结果
3.1 数据集和实验设置
本文使用15类场景数据集。该数据集共有4 485幅图像,包括15个场景类别,分别为:bedroom(216),CALsuburb(241),industrial(311),kitchen(210),livingroom(289),MITcoast(360),MITforest(328),MIThighway(260),MITinsidecity(308),MITmountain(374),MITopencountry(410),MITstreet(292),MITtallbuilding(356),PARoffice(215),store(315)。所有的实验均是在灰度图像上进行,对数据集重复进行5轮随机实验,每一轮都是随机划分训练集和测试集图像(每轮实验中,每类随机选取100幅图像作为训练集,剩下的图像作为测试集)。使用平均识别率ARR(Average Recognition Rate)来评价数据集中每类的最终实验结果。
3.2 实验结果
表1列出了未使用PCA时在5类场景数据集上所得出的实验结果。使用PCA对各个特征向量进行降维,图2和图3分别显示了4种特征和融合特征使用PCA后随着选用降维参数n的不同实验结果的变化曲线图,其中横轴为n,纵轴为平均识别率ARR,对于每个n值,调整分类器参数C的值,使得在该n值下ARR最高,并把最高的ARR值作为取该n值时的实验结果。从图2和图3可知,随着降维维数的不同,最终的结果变化很大,取每个特征的最高的ARR作为之后的比较。另外,图3中可看出当维数降到50维时,ARR达到最高0.77,比之前未使用PCA的结果提升了很多,归结于原来的特征向量里含有冗余信息和噪声,降维之后,这些无关信息被滤除,从而提升了最终的结果。

表1 未使用PCA实验结果
基于上述实验结果得到表2。对于每种特征,随着特征向量所降到的维数不同,分类的准确率也不同。对于单独的特征向量,使用PCA之后得到的分类准确率一般都会降低,这是因为这些特征维数不高,特征向量里面冗余信息不多,降维后有可能去除了一些对图像表示有用的信息。但对于SIFT,加入PCA对特征向量降维后,分类准确率得到了提高,这是因为SIFT特征具有很高的维数,里面包括冗余信息,在降维的过程中去除了冗余信息和噪声,使得分类准确率得以提升。
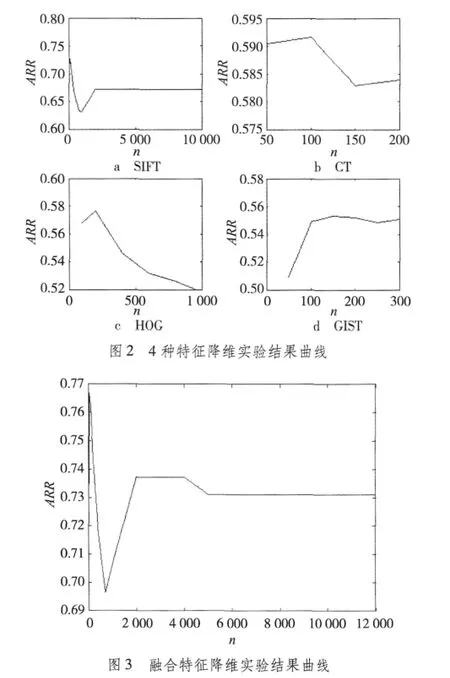
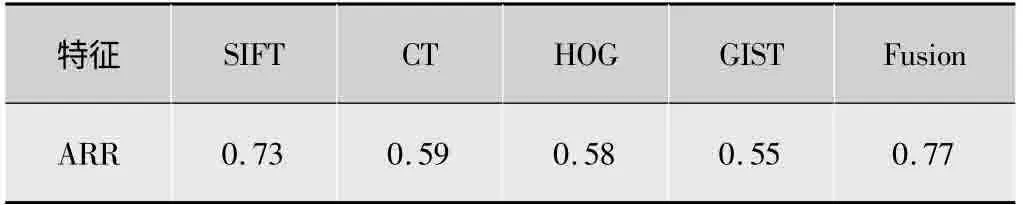
表2 使用PCA实验结果
4 结论
本文中,考虑到在使用高维的特征向量来表示图像时,可能会包含冗余信息,如果把几种不同的特征向量融合到一起,不同的特征之间可能含有重叠的信息,融合的特征向量包含大量的冗余信息,所以提出了使用PCA对特征向量进行降维以达到去除冗余信息和噪声的目的。基于实验结果,得出结论:1)对于维数不高的单个特征向量,在降维后一般ARR都会下降,这是因为把一部分有用信息给去除了;2)但对于维数很高的单个特征向量和融合之后的特征向量,降维后可以把一些冗余信息去掉,从而提高了ARR。
[1]LI F F,PERONA P.A Bayesian Hierarchical Model for Learning Natural Scene Categories[C]//Proc.CVPR 2005.[S.l.]:IEEE Press,2005:524-531.
[2]LAZEBNIK S,SCHMID C,PONCE J.Beyond bag of features:Spatial pyramid matching for recognizing natural scene categories[C]//Proc.CVPR 2006.[S.l.]:IEEE Press,2006:2169-2178.
[3]WU J,REHG J M.CENTRIST:A visual descriptor for scene categorization[C]//Proc.IEEE Transactions on Pattern Analysis and Machine Intelligence 2009.[S.l.]:IEEE Press,2009:1489-1501.
[4]LU F,YANG X,LIN W,et al.Image classification with multiple feature channels[J].Optical Engine,2011,50(5):57-67.
[5]VARMA M,RAY D.Learning the discriminative power-invariance trade-off[C]//Proc.ICCV 2007.[S.l.]:IEEE Press,2007:1-8.
[6]CHRISTOPHER J C.A tutorial on support vector machines for pattern recognition[J].Data Mining and Knowledge Discovery,1998(2):121-167.
[7]LOWE D G.Object recognition from local scale-invariant features[C]//Proc.seventh the International Conference on Computer Vision.[S.l.]:IEEE Press,1999:1150-1157.
[8]OLIVA A,TORRALBA A.Modeling the shape of the scene:a holistic representation of the spatial envelope[J].International Journal of Computer Vision,2001,42(3):145-175.
[9]BOSCH A,MUNOZ X,Marti R.A review:which is the best way to organize/classify images by content?[J].Image and Vision Computing,2007,25(6):778-791.
[10]Principal component analysis:Wikipedia[EB/OL].[2012-10-13].http://en.wikipedia.org/wiki/Principal_component_analysis#cite_note-0.
[11]PEARSON K.On lines and planes of closest fit to systems of points in space[J].Philosophical Magazine,1901,2(6):559-572.
[12]WU J,REHG J M.Where am I:place instance and category recognition using spatial PACT[C]//Proc.CVPR 2008.[S.l.]:IEEE Press,2008:1-8.
[13]LI F F,FERGUS R,PERONA P.Learning generative visual models from few training examples:an incremental Bayesian approach tested on 101 object categories[C]//Proc.CVPR 2004.[S.l.]:IEEE Press,2004:178.
