基于边信息的分布式视频压缩感知的残差重构

胡育涛，钱 慧，余 轮

(福州大学 物理与信息工程学院，福建 福州350002)

传统视频编解码算法(MPEG，H.26x)的复杂度集中在编码端，编码端的复杂度是解码端的5～10倍，适合一些编码端有较强运算能力的场合。但是这种编码器因其编码端的高复杂度很难适用于无线传感器网络，如移动视频摄像等使用小型、低功耗的便携设备中。分布式视频编码(DVC)［1］技术是为了适应低复杂的编码而出现的视频编码框架，它利用视频信号的时间、空间相关性，结合Slepian-Wolf［2］无损编码理论和Wyner-Ziv［3］有损编码理论，把复杂的运动估计、运动补偿技术从编码端转移到解码端。

然而，目前大多数的DVC采用DCT变换编码的方法压缩信息。该种方法通常对非关键帧进行DCT变换，然后利用边信息和非关键帧之间的相关关系压缩视频信号的DCT系数。该种处理方法在对视频信号进行变换后再抛弃冗余数据，因此DCT变换环节存在大量的信号处理冗余。

近几年来，以“边变换边压缩”为思想的压缩感知(Compressive Sensing，CS)［4-5］理论越来越受到人们的关注，是当前信号处理领域的一个研究热点。压缩感知理论认为［6］:只要信号是可压缩的或是在某个变换域是稀疏的，此时可以利用测量矩阵将此高维信号投影到低维空间上，然后利用这些少量的投影值使用求解算法重构出原始信号。压缩感知的显著特点是把变换与压缩有效地结合起来，从而降低编码端的复杂度，提高编码效率。

2009年Baron等人提出了分布式压缩感知的概念(DCS)［7］，它把压缩感知理论扩展到分布式相关信源编码中。分布式压缩感知与传统压缩感知不同，它是建立在信号集“联合稀疏(Joint Sparity Model，JSM)”的假设之上，利用信号间的相关性进行编解码。在视频序列中，同一场景的视频图像之间具有较强的相关性，可以把它们看作是一种特殊的相关信源，Thong T.Do提出的DISCOS［8］和Kang提出的DCVS都属于分布式视频压缩感知(Distributed Compressive Video Sensing)［9］，所不同的是Thong T.Do对关键帧采用帧内编码，非关键帧采用CS编码，而Kang则是两种帧都采用了CS编码。同时，使用当前帧与参考帧差值的稀疏性进行残差重构［10］，也可以使重构质量有所提高。

1 分布式压缩感知

假设长度为N的信号x∈RN，在某个正交基Ψ(如小波基、DCT基)下是稀疏或是可压缩的，则x可表示为x=ΨTθ，其中θ是信号x在正交基下的变换系数，如果θ大于0的个数为K，若K≤N，则称θ为K稀疏。如果存在一个与Ψ不相关的测量矩阵Φ(M×N)，那么根据式(1)可得到x的测量值y。编码见式(1)

解码见式(2)

式中:y是1个M×1的向量(M≪N)，可定义测量率MR=M/N。

解码端根据接收到的测量值y，根据式(2)解l0范数优化问题得到重构系数θ，其中求解l0范数优化问题的本质是一个NP难的问题，计算复杂，求解较难，因此Donoho［4］将此问题用l1范数进行求解，求解方法有贪婪追踪法(OMP［11］)、梯度投影法(GPRS［12］)等，然后根据求得的θ反变换后得到原始信号X。同时S.Mun等使用平滑投影LandWeber算法(Smoothed Projected LandWeber，SPL)［13］取得较好的效果。

分布式压缩感知(DCS)理论建立在信号群的“联合稀疏”的概念上，其主要思想是在编码端利用联合稀疏模型对每个信号进行独立观测和编码，取得较少的观测数量，而在解码端利用各个信号间的相关性进行联合解码。Baron在DCS中定义了3种不同的联合稀疏模型［7］，分别适用于3种不同场合，其中JSM-3更适合视频信号。

针对JSM-3的描述如下

式中:zC=ΨθC代表公共部分;zUj=ΨθUj代表了每个信号的特有部分。在这里，信号的公共部分不一定在基Ψ上稀疏，而特有部分在基Ψ上稀疏的，因此，在解码时需要利用它们之间的共有公共部分压缩信息，然后进行联合解码，如果两个信号之间的相关性越强，那么联合重构出的效果也会越好。本文通过构建两个相关性很强的视频信号用以重构原始的视频信号。

2 基于边信息的分布式视频压缩感知的残差重构

2.1 残差重构的基本思想

2.2 边信息对重构效果的影响

边信息产生方法有直接平均值、前向运动估计、后向运动估计，双向运动估计等。本文产生边信息的方法是运动补偿内插法［14］，它在内插过程中，利用前后相邻(Xi-1，Xi+1)已解码图像，通过一系列的操作使运动矢量尽可能接近运动目标的真实运动轨迹，使产生的边信息(Yi)更接近目标帧。

本文对视频信号采用基于块的CS测量，块大小为32×32，采用独立同分布的高斯随机矩阵ΦB作为测量矩阵，分别用前一帧、后一帧、平均值、运动补偿内插［14］作为边信息得到各个块的残差重构，其重构信号的PSNR如图1所示。虽然运动补偿内插法生成的边信息与原始视频信号相似性更高，但从图中可以看出此方法的边信息重构的效果在有些块上会比其他方法的边信息重构的效果差，为此在编码端利用简单的“块相似性判断”决定每个块使用哪种方法生成边信息，从而提高重构质量。通过对运动补偿内插产生的边信息进行优化，这样能使优化后的边信息与原始视频帧的相关性更强，使它们之间的差值更加稀疏，从而使重构的效果更好。

图1 foreman.cif的第2帧，CS块采样率MR=50%，不同方法的边信息得到各个块的重构效果比较

2.3 提出的视频框架

通过上面的分析，本文提出一种新的基于边信息的分布式视频压缩感知的残差重构方案，如图2所示。

2.3.1 编码端

依据DVC的基本思想，对关键帧采用传统的帧内编码，而非关键帧采用基于块的CS测量得到测量值yj。其中在“块相似性判断”部分，对相邻视频块间进行简单的相似性判断，即对当前非关键的第i帧的第j块(xi，j)与前(xi-1，j)、后(xi+1，j)帧的相应块及其平均值((xi-1，j+xi+1，j)/2)分别进行差值运算，设定一个阈值T，根据3个差值中是否存在最小值小于T，发送一个标志位作为解码端边信息的优化，在本文中定义标志位flag的值为［0，1，2，3 ］分别表示与xi，j最相似的块不存在或者是xi-1，j，xi+1，j，(xi-1，j+xi+1，j)/2。

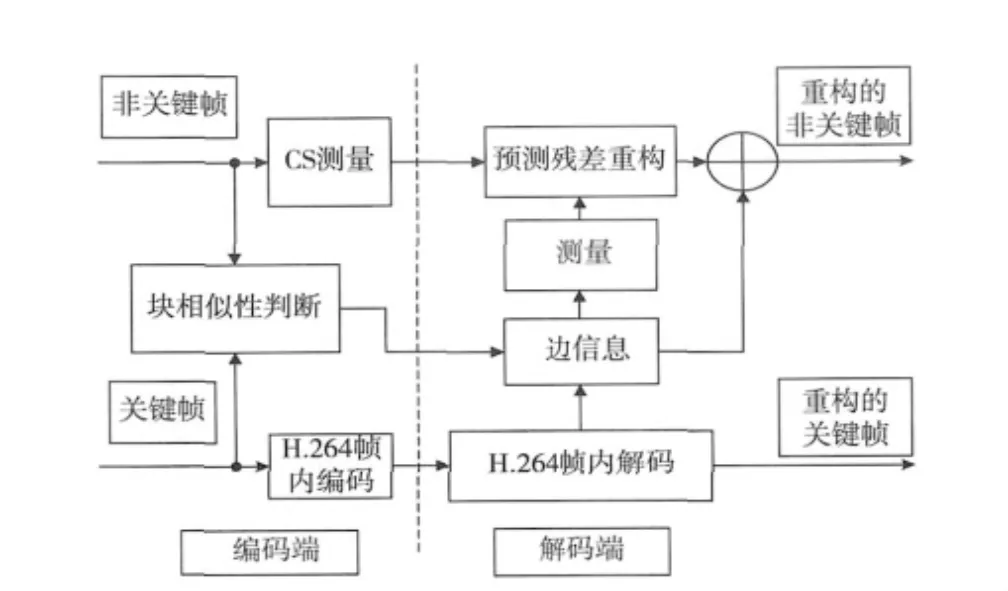
图2 基于边信息的分布式视频压缩感知的残差重构框架

2.3.2 解码端

根据收到的标志位(flag)对运动补偿内插法产生的边信息进行优化，优化方法为

式中:x'i-1，j，x'i+1，j分别表示当前预测帧块通过帧内解码的前、后帧块，这样就得到了优化后的预测帧，它与原始帧有更好的相关性。

对优化后的边信息进行基于块的测量，对于第i帧的第j块有测量值，因此，可以得到随机投影域的残差yri，j，即

式中:xri，j表示原始视频帧块xi，j与预测块之间的差值;yi，j为所接收到的测量值，但是在这里xi，j是未知的。最后利用SPL算法得到重构的预测差值xri，这样就得到了对原始帧的估计，即

具体的解码算法步骤为:

1)根据已解码的关键帧，利用运动补偿内插法生成初始边信息;

2)利用式(4)进行边信息优化;

3)对每个块j有

5)利用SPL算法得到重构的预测差值xr;

3 仿真实验结果

为了验证本文所提出的压缩编码方法对边信息的处理能力，本文选取视频测试序列运动细节较多的foreman.cif和运动细节较少的coastguard.cif各100帧，视频图像组GOP=2，其中关键帧为奇帧，非关键帧为偶帧，选择块的大小为32×32，对于测量矩阵采用独立同分布的高斯随机矩阵ΦB，使用DCT作为CS的变换基，CS的重构方法为SPL算法，使用峰值信噪比(PSNR)来衡量重构的视频质量。图3显示了本文方法与DISCOS［8］和DCVS［9］的方法得出的不同观测率下恢复的非关键帧性能的比较，从图中可以看出本文提出的方法在运动细节较为丰富的foreman.cif中较之DISCOS重构质量有所下降但对于DCVS方法却有很大的提高，在运动细节较少的coastguard.cif上性能比DISCOS的质量提高了4～6 dB，这是因为在foreman.cif中得到的边信息与非关键帧的相关性较低，而coastguard.cif中它们之间的相关性较高。

图3 本文方法与DISCOS，DCVS的方法进行性能对比

4 结束语

本文提出了一种基于边信息的分布式视频压缩感知的残差重构方案，利用边信息与原始帧之间残差值的稀疏性来降低采样率，并使用一种简单、有效的残差重构方法。实验证明该方法对运动细节较少的视频有较大的提高。在后面的研究中，如何进行观测值的量化和编码将是重点。

［1］GRIOD B，ARON A，RANE S.Distributed video coding［J］.Proceedings of the IEEE，2005，93(1):71-83.

［2］SLEPIAN J D，WOLF J K.Noiseless coding of correlated information sources［J］.IEEE Trans.Information Theory，1973，19(4):471-480.

［3］WYNER A D.Recent results in the shannon theory［J］.IEEE Trans.Information Theory，1974，20(1):2-10.

［4］DONOHO D L.Compressive sensing［J］.IEEE Trans.Information Theory，2006，52(4):1289-1306.

［5］CANDES E，ROMBERG J，TAO T.Robust uncertainty principles:exact signal reconstruction from highly incomplete frequency information［J］.IEEE Trans.Information Theory，2006，52(2):489-509.

［6］石光明，刘丹华，高大化，等.压缩感知理论及研究进展［J］.电子学报，2009，37(5):1070-1081.

［7］BARON D，WAKIN M B，DUARTE M，et al.Distributed compressed sensing［EB/OL］.［2012-10-02］.http://dsp.rice.edu/publications/distributed-compressed-sensing.

［8］DO T T，CHEN Y，NGUYEN D T，et al.Distributed compressed video sensing［C］//Proc.CISS 2009.［S.l.］:IEEE Press，2009:1393-1396.

［9］KANG L W，LU C S.Distributed compressive video sensing［C］//Proc.ICASSP 2009.Washington DC:IEEE Computer Society，2009:1169-1172.

［10］朱向军，冯志林，王洁，等.运动补偿预测残差稀疏重构的压缩视频传感［J］.电视技术，2012，36(9):7-9.

［11］TROPP J，GILBERT A.Signal recovery from random measurements via orthogonal matching pursuit［J］.IEEE Trans.Information Theory，2007，53(12):4655-4666.

［12］FIQUEIREDO M A T，NOWAK R D.Gradient projection for sparse reconstruction:application to compressed sensing and other inverse problems［J］.IEEE Journal of Selected Topics in Signal Processing，2007，1(4):586-597.

［13］MUN S，FOWLER J E.Block compressed sensing of images using directional transforms［C］//Proc.DCC 2010.［S.l.］:IEEE Press，2009:3021-3024.

［14］ASCENSO J，BRITES C，PEREIRA F.Improving frame interpolation with spatial motion smoothing for pixel domain distributed video coding［C］//Proc.5th EURASIP Conference on Speech and Image Processing，Multimedia Communications and Services.［S.l.］:Slovak Republic，2005:21-26.