校正的Bootstrap方法对概化理论方差分量及其变异量估计的改善*
2013-01-31黎光明张敏强
黎光明 张敏强
(1华南师范大学心理应用研究中心,广州 510631) (2广州大学教育学院心理系,广州 510006)
1 引言
概化理论,又称为方差分量模型,在心理与教育测量实践中有着广泛的应用。Bootstrap方法,也称“自助法”,是一种有放回的再抽样方法,可用于概化理论的方差分量及其变异量估计(Brennan,2001)。
Bootstrap方法是美国斯坦福大学统计系Efron(1979)提出的一种统计方法。这种方法是统计学上的新突破之一(Fan,2003),其实质是模拟了从原始数据(把它看作“总体”)中随机抽取大量样本的过程,既可以用于参数估计,也可用于非参数估计(Cui &Kolen,2008)。使用Bootstrap 方法的基本程序是:以原始数据(样本容量为n
) 为基础,在保证每个观察单位每次被抽到的概率相等(1/n
)的情况下,作有放回的重复抽样,所得样本被称为Bootstrap样本。根据一个 Bootstrap样本计算出相应的统计量,就得到参数的一个估计值。这样重复若干次(记为 B,常设 B = 1000),就形成了一个参数的近似抽样分布。根据这个抽样分布,可以估计出平均值、标准差、相应的百分位数,进而获得参数的标准误和置信区间。在这个过程中,如果频数分布是正态的,可以用参数的标准误直接计算其95%置信区间。如果频数分布不是正态的,可以用第 2.5百分位数和第97.5百分位数来估计其95%置信区间。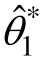
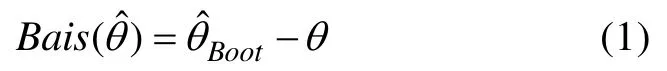


虽然上述 Bootstrap方法过程比较简单,但是如何进行 Bootstrap方法再抽样却是个问题。这是因为对于完全随机的p×i设计存在多种抽样,不同的抽样方法抽取样本不同,可能导致计算出的统计量(如标准误)有别。因此,需要对 Bootstrap方法再抽样进行考虑,包括再抽样策略和未校正与校正策略。
第一,再抽样策略。因为是完全随机的 p×i设计,进行再抽样既要考虑p和i,也要考虑残差项r。根据 Bootstrap再抽样原则,可供考虑的 Bootstrap策略有10种(Wiley,2001),分别是boot-p、boot-i、boot-pi、boot-pr、boot-ir、boot-pir、boot-effects、boot-oneway、boot-individual和 boot-main。前 7种再抽样策略是“单一”的再抽样策略,后3种再抽样策略是“综合”的再抽样策略。其中boot-p表示固定i和r,仅考虑对p抽样; boot-i表示固定p和r,仅考虑对i抽样; Boot-pi表示固定r,对p和i同时抽样; Boot-pr表示固定i,考虑对p和r抽样; boot-ir表示固定p,考虑对i和r抽样; boot-pir表示考虑对p、i和r同时抽样; Boot-effects表示用“概率机制”P来抽取随机效应样本的一种方法(Efron & Tibshrani,1993; Wiley,2001; Othman,1995); boot-oneway是一种再抽样策略,要求对比 p和 i的样本容量,按照较大者进行“单一”的再抽样策略,如 boot-p或boot-i,但不可能是boot-pi (Leucht & Simth,1989)。boot-individual表示对 p使用 boot-p,对 i使用boot-i,对pi使用boot-pi,而boot-main则表示对p和pi使用boot-p,对 i使用 boot-i (Othman,1995)。Wiley (2001)认为boot-effects对于不平衡的数据不适合,因此这种再抽样策略在实践中受到限制。在考虑残差抽样的几种策略(boot-pr、boot-ir、boot-pir)中,r被作为一个随机因素。
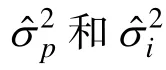

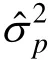

公式(5)和(6)其实与Brennan等人(1987)乘以校正系数估计方差分量等价。
Brennan,Leucht和Othman等人均认为对概化理论方差分量的估计存在“最佳”的Bootstrap策略。但是,Wiley (2001)给出了完全随机的p×i设计下各种再抽样策略下的校正公式推导,否定了这种说话,即对于方差分量估计不存在“最佳”情况。也就是说,如果对原来 Bootstrap方法再抽样策略进行校正,那么所有再抽样策略都能够准确估计方差分量。Wiley (2001)的研究具有极其重要的意义,Wiley从理论上推导出如何对各种再抽样策略进行有效校正。Wiley (2001)认为在完全随机的p×i设计下,虽然 Bootstrap方法进行方差分量点估计不存在“最佳”策略,但对于方差分量变异量的估计情况就不同了。因此,需要探讨未校正的Bootstrap方法和校正的 Bootstrap方法对于估计方差分量标准误和置信区间之间存在的差别。本研究借鉴和改进了Wiley的成果,进一步采用了校正的Bootstrap方法来估计概化理论方差分量的变异量。

根据 Bootstrap方法的实现过程,一些学者(Leucht & Smith,1989; Othman,1995; Brennan,2001; Wiley,2001)已注意到,虽然Bootstrap方法乘以一定校正系数后对方差分量估计有所改善,但存在以下问题:
第一,未见学者对于校正的 Bootstrap方法是否改善概化理论方差分量变异量估计,作出详细讨论。Wiley (2001)注意到校正的Bootstrap方法对于方差分量估计具有等价性(equivalence),这种等价性表现在各种校正的Bootstrap策略估计的方差分量相当一致。但这却不能拓广至方差分量变异量。然而,Wiley的研究仅是比较了各种Bootstrap策略,却没有对校正的与未校正的Bootstrap方法进行比较。
第二,鲜有学者真正意义上对非正态分布数据进行过比较,特别是对校正的和未校正的Bootstrap方法。Brennan、Leucht、Othman和 Wiley等人的研究,用模拟数据进行方法之间的比较,仅限于正态分布数据。但是,非正态分布数据具有常见性,一些考试数据,如选择题,就是0或1记分,是二项分布数据,一些心理测验数据,用Likert形式评分,如 0~4分,就是多项分布数据,缺乏探讨非正态分布数据形式下方法之间的比较,显得不足。
第三,一些学者的研究仍不充分。黎光明和张敏强(2009a)认为,数据分布对概化理论方差分量变异量估计有影响,与 Traditional、Jackknife、MCMC三种方法相比,Bootstrap方法具有方法的“跨分布性”,但是这种性质是建立在 Bootstrap方法“分而治之”策略之下,boot-p、boot-pi、boot-i策略分别估计p、i、pi的方差分量变异量最佳。然而,boot-p、boot-pi、boot-i策略是使用校正的方法好,还是使用未校正的方法好,未作出进一步的讨论和说明。
即使 Bootstrap方法具有方法的“跨分布性”,且具有统一规则,也仅仅解释了如何使用Bootstrap方法的问题。对于Bootstrap的 boot-p、boot-pi、boot-i策略如何选择方差分量标准误和置信区间估计方法,却是一个值得更为深入讨论的问题。Wiley (2001)认为,未校正的Bootstrap方法与校正的 Bootstrap方法在变异量估计上相当。这个结论是粗糙的,从整体而言,并没有完全针对某一种 Bootstrap策略进行深入研究,更忽略了两种方法在方差分量变异量估计上的精确比较。因此,需要更为深入地探讨,在多种数据分布下(如正态分布、二项分布、多项分布和偏态分布),校正的Bootstrap方法估计概化理论方差分量及其变异量是否优于未校正的Bootstrap方法。或者说,跨越不同数据分布,相比于未校正的Bootstrap方法,校正的 Bootstrap方法是否对概化理论方差分量及其变异量估计有所改善。
2 方法
2.1 数据产生
基于 p×i设计概化理论模型,运用蒙特卡洛数据模拟技术产生各种分布数据。数据模拟所使用的软件为R软件,产生的模拟数据包括:正态分布、二项分布、多项分布和偏态分布数据。
2.2 比较标准

2.3 分析工具
分析工具为R软件和HyperbolicDist软件包。借助这些软件或软件包,自编完成研究程序。通过自编的R程序,产生1000批次的模拟数据,直接实现 Bootstrap方法对方差分量及其变异量的估计,HyperbolicDist软件包的作用在于生成服从一定偏度的偏态分布数据。
3 结果
3.1 不同分布数据的方差分量偏差
对正态、二项、多项和偏态分布模拟数据,分别计算校正的和未校正的Bootstrap方法的boot-p、boot-i、boot-pi策略估计的三个方差分量偏差(如表1)。通过比较估计的方差分量偏差,可以看出不同数据分布下不同方法估计方差分量的性能差异。
表1中 vc.p_bias、vc.i_bias、vc.pi_bias分别表示人的方差分量偏差、题目的方差分量偏差、人与题目交互作用(包括残差)的方差分量偏差。adjust和non-adjust分别表示校正的和未校正的Bootstrap方法。boot-p、boot-i、boot-pi表示 Bootstrap方法的三种策略。Normal、Dichotomous、Polytomous、Skewnessed分别表示正态分布、二项分布、多项分布和偏态分布数据。表 1中的数值表示使用Bootstrap方法所得的方差分量偏差,这些偏差是将估计值与参数值相减后获得的,例如,0.0289表示对正态分布数据使用校正的 Bootstrap方法的boot-p策略估计的方差分量为 4.2089,参数值为4.000,两者相减后即为0.0289。又如,−0.0114表示对正态分布数据使用未校正的 Bootstrap方法的boot-p策略估计的方差分量为 3.9886,参数值为4.000,两者相减后即为−0.0114,其它类似解释。
3.2 不同分布数据的方差分量标准误偏差
对正态、二项、多项和偏态分布模拟数据,分别计算校正的和未校正的Bootstrap方法的boot-p、boot-i 、boot-pi策略估计的三个方差分量标准误偏差(如表 2)。通过比较估计的方差分量标准误偏差,可以看出不同数据分布下不同方法估计方差分量标准误的性能差异。
表2中 SE (vc.p)_bias、SE (vc.i)_bias、SE(vc.pi)_bias分别表示人的方差分量标准误偏差、题目的方差分量标准误偏差、人与题目交互作用(包括残差)的方差分量标准误偏差。其它解释同表1。例如,−0.0192表示对正态分布数据使用未校正的Bootstrap方法的 boot-p策略估计的方差分量标准误为 1.0095,参数值为 1.0287,两者相减后即为−0.0192,其它类似解释。
3.3 不同分布数据的方差分量置信区间包含率
对正态、二项、多项和偏态分布模拟数据,分别计算校正的和未校正的Bootstrap方法的boot-p、boot-i、boot-pi策略估计的三个方差分量置信区间包含率(如表 3)。通过比较估计的方差分量置信区间包含率,可以看出不同数据分布下不同方法估计方差分量置信区间的性能差异。
表3中 CI (vc.p)、CI (vc.i)、CI (vc.pi)分别表示人的方差分量置信区间包含率、题目的方差分量置信区间包含率、人与题目交互作用(包括残差)的方差分量置信区间包含率。其它解释同表 1。例如,0.769表示对正态分布数据使用未校正的Bootstrap方法的 boot-p策略估计的方差分量置信区间包含率,其它类似解释。计算80%置信区间包含率的方法是:通过判断参数是否落入10%到90%两分位点对应的方差分量之间,如果某次成功,则包含次数加 1,最后计算落入的总次数,并除以 1000,即为最后的包含率。
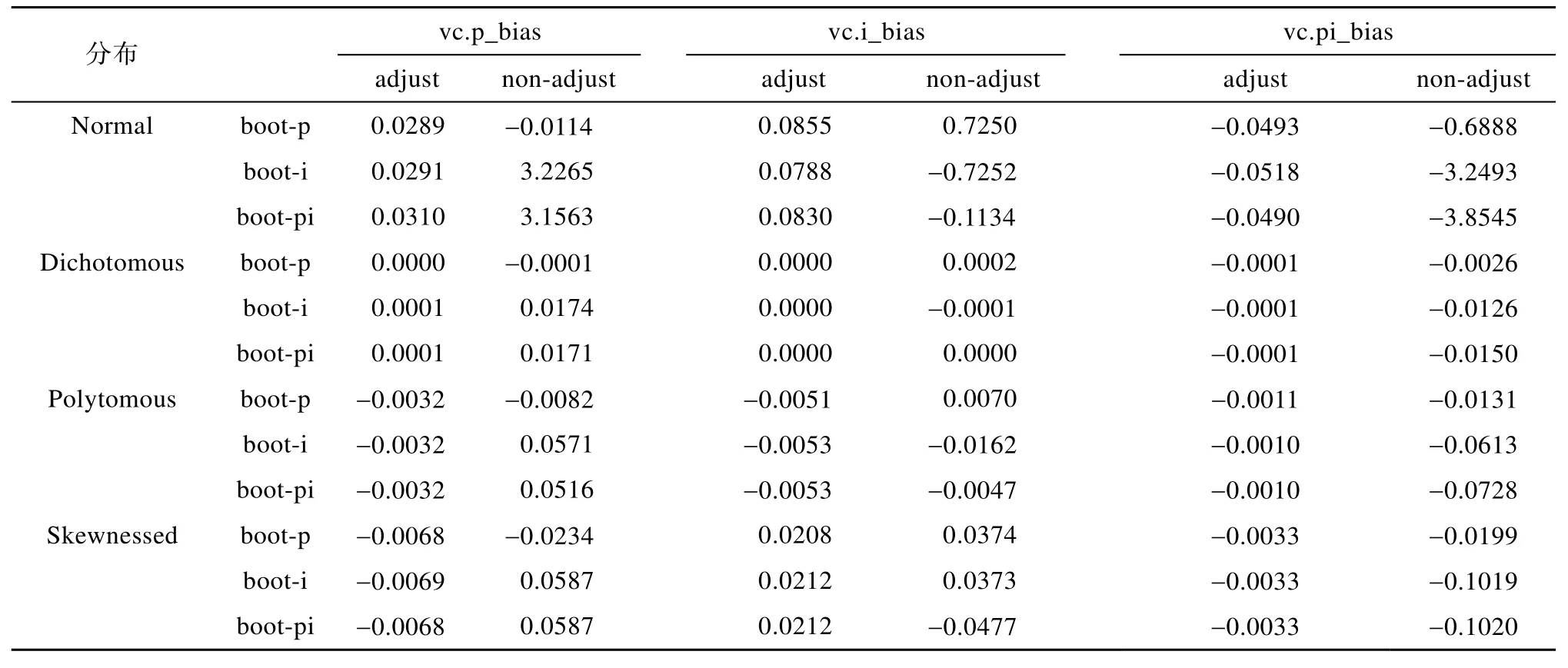
表1 不同分布数据Bootstrap方法估计的方差分量偏差

表2 不同分布数据Bootstrap方法估计的方差分量标准误偏差
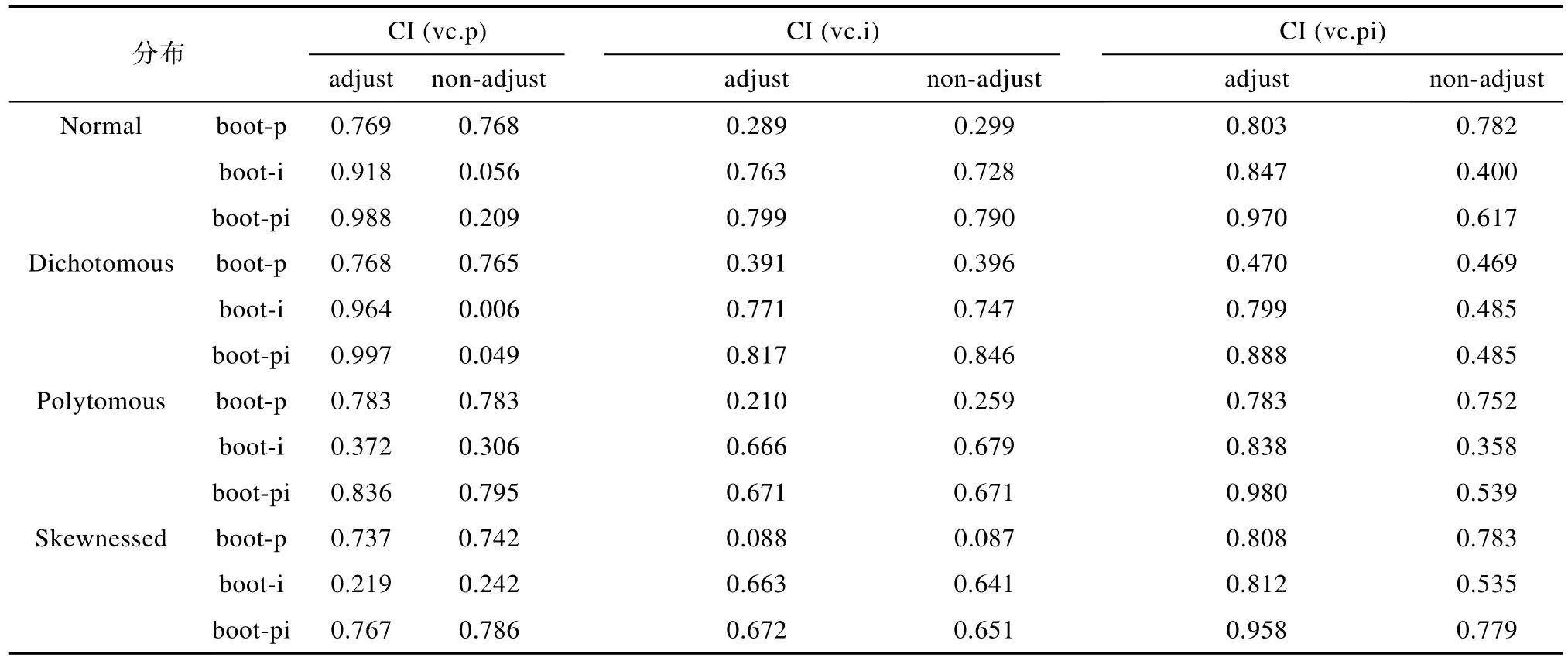
表3 不同分布数据Bootstrap方法估计的方差分量置信区间包含率
4 分析与讨论
4.1 不同分布数据的方差分量偏差分析
根据表 1中四种分布数据 Bootstrap方法的boot-p、boot-i 、boot-pi策略估计的三个方差分量偏差,可以绘出它们对应的偏差图,如图1(a)~(d)所示。
从图 1(a)可以看出,对于正态分布数据,在人的方差分量偏差上,未校正的boot-pi和boot-i策略偏差分别为3.2265和3.1563,相对较大,远离横轴,未校正的boot-p策略偏差为-0.0114,相对较小,几乎接近横轴,校正的boot-p、boot-i、boot-pi策略偏差分别为 0.0289、0.0291、0.0310,相对较小。在题目的方差分量偏差上,未校正的 boot-pi策略偏差相对较小,未校正的boot-i和boot-p策略偏差相对较大,校正的boot-p、boot-i 、boot-pi策略偏差相对较小。在人与题目交互作用(包括残差)的方差分量偏差上,未校正的boot-p、boot-i、boot-pi策略偏差相对较大,校正的boot-p、boot-i、boot-pi策略偏差相对较小。对图 1(a)的分析可知,对于正态分布数据,校正的 Bootstrap方法各种策略估计方差分量较为接近,策略间具有“等价性”,这与 Wiley(2001)的结论一致。

图1 正态、二项、多项和偏态分布数据Bootstrap方法估计的方差分量偏差图
从图 1(b)可以看出,对于二项分布数据,在人的方差分量偏差上,未校正的 boot-p、boot-i、boot-pi策略方差分量偏差相对较大,校正的boot-p、boot-i、boot-pi策略方差分量偏差相对较小。在题目的方差分量偏差上,校正的和未校正的boot-p、boot-i、boot-pi策略方差分量偏差相当,相对较小。在人与题目交互作用(包括残差)的方差分量偏差上,校正的boot-p、boot-i、boot-pi策略方差分量偏差相对较大,校正的boot-p、boot-i、boot-pi策略偏差相对较小。
从图 1(c)可以看出,对于多项分布数据,其解释可参考图1(a)。
从图 1(d)可以看出,对于偏态分布数据,在人的方差分量偏差上,未校正的 boot-p、boot-i、boot-pi策略方差分量偏差相对较大,校正的boot-p、boot-i、boot-pi策略方差分量偏差相对较小。在题目的方差分量偏差上,未校正的 boot-pi策略方差分量偏差相对较大,未校正的boot-p和boot-i策略方差分量偏差相当,校正的 boot-p、boot-i、boot-pi策略方差分量偏差相当,表现出 Wiley(2001)提出的“等价性”。但是,值得注意的是,偏差并没有接近横轴,这与图 1(a)~(c)结果不一致,这说明数据的“偏态性”会影响数据的方差分量估计精度,这是一些研究未注意到的地方(Othman,1995; Wiley,2001; Tong & Brennan,2007),对比校正的和未校正的 boot-p、boot-i、boot-pi在题目上的方差分量偏差,前者仍然小于后者。在人与题目交互作用(包括残差)的方差分量偏差上,未校正的boot-p、boot-i、boot-pi策略偏差相对较大,校正的boot-p、boot-i、boot-pi策略方偏差相对较小。
4.2 不同分布数据的方差分量标准误偏差分析
根据表 2中四种分布数据 Bootstrap方法的boot-p、boot-i、boot-pi策略估计的三个方差分量标准误偏差进行配对样本的 t检验,boot-p、boot-i、boot-pi策略各有12对数据,这样总共有36对数据,对这36对数据进行t检验(张厚粲,徐建平,2004),结果为t
=2.021,p
=0.051,表明差异显著性检验相伴概率处于边缘显著水平(0.050 <p
< 0.100),从总体趋势看,可以认为校正的和未校正的 boot-p、boot-i、boot-pi策略在三个方差分量的标准误偏差存在差异,前者的偏差小于后者的偏差。从表 2可以看出,对于正态分布数据,校正的和未校正的 boot-p策略估计人的方差分量标准误偏差分别为-0.0192和-0.0293,绝对偏差相对较小,而校正的和未校正的boot-i策略估计人的方差分量标准误偏差分别为0.4687和0.4204,校正的和未校正的 boot-pi策略估计人的方差分量标准误偏差分别为 1.0676和 1.0024,绝对偏差相对较大。因此,可以认为,对于正态分布数据,boot-p策略估计人的方差分量标准误最佳。同理,boot-pi策略估计题目的方差分量标准误最佳,boot-p策略估计人与题目交互作用(包括残差)的方差分量标准误最佳,boot-i策略次佳。
在表 2中,依照正态分布数据的分析方法,对于二项和多项分布数据,boot-p策略估计人的方差分量标准误最佳,boot-pi策略估计题目的方差分量标准误最佳,boot-i策略估计人与题目交互作用(包括残差)的方差分量标准误最佳。对于偏态分布数据,boot-pi策略估计人的方差分量标准误最佳,boot-p策略次佳,boot-pi策略估计题目的方差分量标准误最佳,boot-i策略估计人与题目交互作用(包括残差)的方差分量标准误最佳。
根据以上分析,整合四种分布数据,boot-p策略估计SE (vc.p)最佳,boot-pi策略估计SE (vc.i)最佳,boot-i策略估计 SE (vc.pi)最佳,这符合Bootstrap方法“分而治之”策略规则。根据这种“分而治之”策略规则,对于概化理论方差分量标准误估计,应该探索是否校正的方法优于未校正的方法,如果前者更好,应该采用校正的方法。接下来,按照“分而治之”策略规则,使用校正的和未校正的方法,分别分析boot-p策略估计SE (vc.p),boot-pi策略估计SE (vc.i),boot-i策略估计SE (vc.pi),结果如图2(a)~(c)所示。
从图 2(a)可以看出,未校正的和校正的 boot-p策略估计p的方差分量标准误偏差不一致,表明两种方法估计 p的方差分量标准误有差别,校正的boot-p策略的标准误偏差更小。与未校正的方法相比,校正的boot-p策略估计p的方差分量标准误相对更为准确。跨越不同分布,发现偏态分布数据估计的标准误偏差最大,然后是正态分布和多项分布,标准误最小是二项分布。跨越不同分布估计的标准误偏差不同,其原因与数据本身有关,例如,正态分布数据与二项分布数据,其标准误是不同的,二项分布数据是1或0的形式,数据本身较小,求出的方差分量较小,其标准误偏差自然也较小。但是,正态分布则不同,它的数据可能较大(如 20),这样的数据产生的方差分量较大,其标准误偏差也较大,其它分布情况类似。

从图2(b)可以看出,未校正的和校正的boot-pi策略估计 i的方差分量标准误偏差存在差别,特别是正态分布数据(Normal),校正的和未校正的boot-pi策略估计 i的方差分量标准误偏差分别是−0.0023和−0.2720,前者绝对偏差值明显小于后者,其它结果与图 2(a)近似,表明未校正的和校正的boot-pi策略估计i的方差分量标准误偏差表现出不一致,从整体上看,校正的方法要优于未校正的方法。在图 2(c)中,不同数据分布下估计的方差分量标准误偏差也存在差别,正态分布数据两种方法差异较大,其它分布差异则不显著。
未校正的和校正的 boot-p、boot-i、boot-pi策略在估计p、i、pi的方差分量标准误时,结果存在差异,校正的方法相对较好,也考虑到校正的boot-p、boot-i、boot-pi策略在方差分量点估计上要优于未校正的boot-p、boot-i、boot-pi策略。因此,不同的数据分布下使用校正的 boot-p、boot-i、boot-pi策略来估计p、i、pi的方差分量标准误,更为妥当些。
4.3 不同分布数据的方差分量置信区间包含率分析
本研究Bootstrap使用了PC方法来估计方差分量置信区间,并用包含率的大小来估价各种Bootstrap策略的准确性,boot-p、boot-i、boot-pi策略隶属于Bootstrap策略,也是采用了PC方法来估计方差分量置信区间。如果包含率越接近0.800,那么结果越准确。
根据表3的结果,为了对比校正的和未校正的Bootstrap方法在估计方差分量置信区间包含率时的差异,我们作了两种方法方差分量置信区间包含率散点图,如图3(a)~(c)所示。
从图 3(a)和图 3(c)可以看出,校正的和未校正的 Bootstrap方法散点无规律性,表明两种方法数据等级之间存在不一致性,两种方法存在差异。从图3(b)可以看出,校正的和未校正的Bootstrap方法散点几乎在一条直线上,两种方法估计题目的方差分量置信区间包含率差异较小。跨越四种分布数据,分别计算CI (vc.p)、CI (vc.i)、CI (vc.pi)校正的和未校正的 Bootstrap方法的相关系数,其值分别为−0.112 (p
=0.729)、0.996 (p
=0.000)、0.174 (p
=0.589),表明校正的和未校正的Bootstrap方法在CI (vc.p)和 CI (vc.pi)存在差异,与上述散点图结果一致。将校正的和未校正的 Bootstrap方法在 CI(vc.p)、CI (vc.i)和CI (vc.pi)的包含率与0.800相减,所得值表示偏差值,偏差越大,表示偏离参数越大,结果越不可靠。用配对样本T检验比较校正的和未校正的 Bootstrap方法包含率的偏差差异,结果如表4所示。
从表4可知,校正的和未校正的Bootstrap方法在CI (vc.p)、CI (vc.i)和CI (vc.pi)的包含率偏差存在显著性差异且效果量相对较大(t
=3.693,p
≤0.001,d
=0.764),与未校正的方法相比,校正方法的包含率偏差更小,这表明从总体上看,校正的Bootstrap方法在估计方差分量置信区间时,优势更为明显。类似于分析方差分量标准误,对于置信区间估计,Bootstrap方法仍然遵循“分而治之”策略。分析这些策略目的是在分析总(整)体结果之后,对局部的考虑,探讨这些策略是否也服从总体所得到的结果。

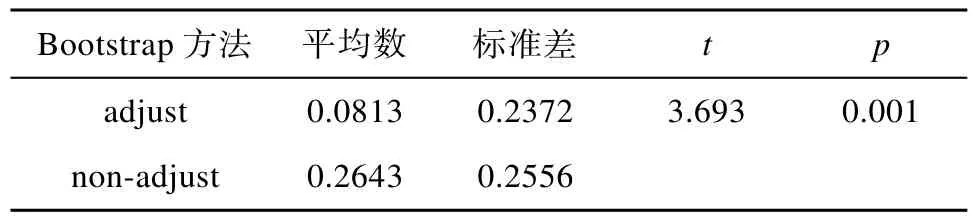
表4 校正的和未校正的 Bootstrap方法包含率偏差的差异显著性检验
与对表2的分析类似,对于表3中的正态和偏态分布数据,boot-p估计CI (vc.p)最佳,boot-pi估计CI (vc.i)最佳,boot-p 估计 CI (vc.pi)最佳,boot-i次佳。对于表3中的二项和多项分布数据,boot-p估计CI (vc.p)最佳,boot-pi估计CI (vc.i)最佳,boot-i估计CI (vc.pi)最佳。综合考虑可认为,跨越四种分布数据,boot-p估计CI (vc.p)最佳,boot-pi估计CI(vc.i)最佳,boot-i估计CI (vc.pi)最佳。
与上述标准误偏差分析类似,在整体分析之后,再考虑“局部”,即根据这种“分而治之”策略规则,对于概化理论方差分量置信区间估计,应该探索是否校正的方法优于未校正的方法,如果前者更好,表明应该采用校正的方法。接下来,按照“分而治之”策略规则,使用校正的和未校正的方法,分别分析boot-p策略估计CI (vc.p),boot-pi策略估计CI(vc.i),boot-i策略估计CI (vc.pi),结果如图4(a)~(c)所示。
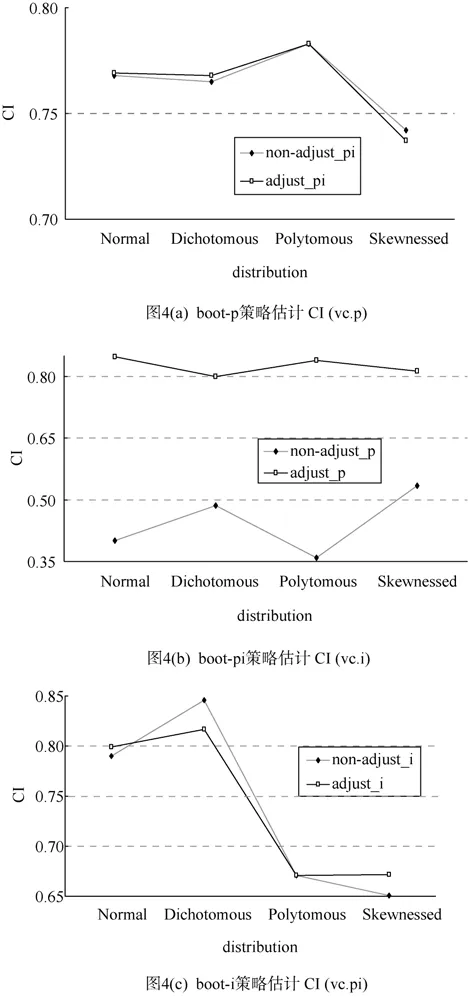
从图4(a)可以看出,boot-p策略估计CI (vc.p),在正态和二项分布数据下,校正的方法与未校正的方法相比,包含率更接近参数值 0.800,表明校正的方法略优于未校正的方法; 在多项分布下,两种方法相当; 在偏态分布下,未校正的方法略优于校正的方法。
从图4(b)可以看出,boot-pi策略估计CI (vc.i),在正态、二项和偏态分布数据下,校正的方法与未校正的方法相比,包含率更接近参数值 0.800,表明校正的方法略优于未校正的方法; 在多项分布下,两种方法相当。
从图4(c)可以看出,boot-i策略估计CI (vc.pi),在正态、二项、多项和偏态分布数据下,校正的方法与未校正的方法相比,包含率更接近参数值0.800,而未校正的方法明显远离参数值 0.800,表明校正的方法明显优于未校正的方法。
5 结论
(1)对于方差分量(点)估计,跨越四种分布数据,与未校正的 Bootstrap方法相比,校正的 Bootstrap方法各种策略估计方差分量较为接近,策略间具有“等价性”,估计的方差分量偏差相对较小。
(2)对于方差分量标准误估计,跨越四种分布数据,从整体趋势看,校正的Bootstrap方法与未校正的 Bootstrap方法估计三个方差分量标准误偏差存在差异,前者的偏差小于后者的偏差。从“分而治之”策略局部看,与未校正的 boot-p、boot-pi和boot-i策略分别估计p、i、pi的方差分量标准误相比,校正的方法相对较好。
(3)对于方差分量置信区间估计,跨越四种分布数据,校正的 Bootstrap方法和未校正的Bootstrap方法包含率偏差存在显著性差异,校正的方法包含率偏差更小,从整体上看,校正的Bootstrap方法优势更为明显。从“分而治之”策略局部看,校正的方法也较好。
(4)对上述结论进一步推论:跨越四种分布数据,从“整体”到“局部”,不论是“点估计”还是“变异量估计”,一致表明:校正的Bootstrap方法要优于未校正的Bootstrap方法,校正的Bootstrap方法改善了概化理论方差分量及其变异量估计。
Brennan,R.L.(2001).Generalizability theory.
New York:Springer-Verlag.Brennan,R.L.(2007).Unbiased estimates of variance components with bootstrap procedures.Educational and Psychological Measurement,67
(5),784–803.Brennan,R.L.,Harris,D.J.,& Hanson,B.A.(1987).The
bootstrap and other procedures for examining the variability of estimated variance components in testing contexts
(ACT Research Report Series87-7).
Iowa City,IA:American College Testing Program.Cui,Z.M.,& Kolen,M.J.(2008).Comparison of parametric and nonparametric bootstrap methods for estimating random error in equipercentile equating.Applied Psychological Measurement,32
(4),334–347.Efron,B.(1979).Bootstrap method:Another look at the jackknife.Annals of Statistics
,7
,1–26.Efron,B.(1982).The jackknife,the bootstrap and other resampling plans
.SIAM CBMS-NSF Monograph 38.Efron,B.,& Tibshrani,R.J.(1986).Bootstrap methods for standard errors,confidence intervals,and other measures of statistical accuracy.Statistical Science,1
, 54–57.Efron,B.,& Tibshrani,R.J.(1993).An introduction to the Bootstrap
.New York.Chapman and Hall.Fan,X.T.(2003).Using commonly available software for bootstrapping in both substantive and measurement analyses.Educational and Psychological Measurement,63
(1),24–50.Gao,X.H.(1992).Generalizability of a state-wide science performance assessment.
Unpublished doctorial dissertation.University of California.Leucht,R.M.,& Smith,P.L.(1989).The effects of bootstrapping strategies on the estimation of variance components.
Paper presented at the annual meeting of the American Educational Research Association,San Francisco,CA.Li,G.M.,& Zhang,M.Q.(2009a).A Cross-distribution study:Estimating the variability of estimated variance components for Generalizability Theory.InThe 1st psychology doctoral forum of china collection of summaries
(pp.290–294).Beijing:Beijing Normal University.[黎光明,张敏强.(2009a).一项跨分布研究:基于概化理论的方差分量变异量估计.见首届全国心理学博士学术论坛论文集(pp.290–294).北京:北京师范大学.]
Li,G.M.,& Zhang,M.Q.(2009b).Estimating the variability of estimated variance components for Generalizability Theory.Acta Psychologica Sinica,41
(9),889–901.[黎光明,张敏强.(2009b).基于概化理论的方差分量变异量估计.心理学报,41(9),889–901.]
Othman,A.R.(1995).Examining task sampling variability in science performance assessments.
Unpublished doctoral dissertation,University of California,Santa Barbara.Tong,Y.,& Brennan,R.L.(2007).Bootstrap estimates of standard errors in generalizability theory.Educational and Psychological Measurement,67
(5),804–817.Wiley,E.W.(2001).Bootstrap strategies for variance component estimation:Theoretical and empirical results.
Unpublished doctoral dissertation,Stanford University,Stanford,CA.Zhang,H.C.,& Xu,J.P.(2004).Modern psychological and educational statistics.
Beijing,China:Beijing Normal University Press.[张厚粲,徐建平.(2004).现代心理与教育统计学.北京:北京师范大学出版社.]
