数学学业不良初中生的工作记忆特点：领域普遍性还是特殊性?*

2013-01-31丹1李其维邓赐平

心理学报 2013年2期

蔡丹1李其维邓赐平

(1上海师范大学教育学院, 上海 200234) (2华东师范大学心理与认知科学学院, 上海 200062)

1 问题提出

在初中数学学业任务所涉及的认知加工研究领域中, 研究者虽然较为一致地肯定数学学业不良会在某些认知机制上存有缺损, 但究竟其缺损发生在哪一部分, 各种研究却众说纷纭, 数学学业不良的核心缺陷尚未得到确认已成为不争的事实(Geary,2004; Mazzocco & Mayers, 2003; Raghubar, Barnes,& Hecht, 2010; de Smedt et al., 2009)。数学学业不良可能因其所依赖的认知缺陷不同还可进行亚类型的进一步细分, Geary (2004), Geary, Hamson和Hoard (2000)将数学学业不良分为语义记忆型、程序型和视觉－空间型; Mazzocco和Mayers (2003)的研究支持了语义记忆型数学学业不良的独立性,但却认为对另外两种亚类型的明确鉴别至少在目前是相当困难的。因此不少研究(李清, 2009; 左志宏,2006)将数学学业不良仅区分为两类, 单纯型(不区分程序型和视觉－空间型)数学困难和混合型(即数学与阅读困难共存的语义记忆型)数学困难。除此之外, 按照数学学习的内容领域来区分数学学业不良逐渐成为一种趋势(陈英和, 2009; 赵燕, 蔡笑岳, 2010)。

工作记忆是一个容量有限的存储加工系统(Baddeley, 1992)。近年来, 中央执行系统、视觉－空间模板及语音环路组成的工作记忆三成分在学业成就中的作用受到越来越多研究者的关注。在数学学习领域, 多位研究者支持三个子系统在其中发挥了重要作用(Andersson, 2010; Fürst & Hitch, 2000;Lee & Kang, 2002; Kyttälä, Aunio, & Hautamäki, 2010;Simmons, Willis, & Adams, 2012)。中央执行系统在工作记忆中起到监控和协调作用, 它在工作记忆模型中占据核心地位。近来, 有关中央执行功能对数学学习影响的研究层出不穷。研究者认为(王恩国,刘昌, 2005), 所有中央执行功能研究都基于两个假设：第一个假设是, 主体在必须成功地协调完成初级任务和次级任务时, 他们只能减少执行加工活动。在负荷任务要求高的加工条件下, 加工协调必须由执行系统来完成, 这些调节主要包括：抑制干扰信息, 选择性注意这两个主要内容。第二个假设是, 面对大量的认知任务, 由于有限的认知加工资源, 被试的成绩会随着任务量和任务难度增加而降低。这些限制是由于长时记忆中信息储存不足和注意能力有限造成的。根据这一思路, 国外学者对数学学业不良儿童的中央执行功能研究目前主要集中在三个方面：项目抑制控制、选择性注意以及和基本数学事实的提取(左志宏, 2006)。中央执行功能对数学学习的影响是毋庸置疑的。但数学学业不良学生究竟在哪一方面的执行功能产生缺损与不足, 不同类别的数学学业不良的中央执行功能是否具有相同的缺损模式, 这些问题仍然值得进一步加以探讨。

除中央执行系统外, 初中生的数学学习与工作记忆的两个附属系统—— 语音环路和视觉－空间模板也存在不同程度的关联。然而, 各种研究却没有统一数学学业不良儿童在视－空模板及语音环路这两个系统中分别缺损的程度, 不同研究支持着不同的立场(Krajewsk & Schneider, 2009; Meyer,Salimpoor, Wu, Geary, & Menon, 2010)。Passolunghi和Siegel (2001)发现, 数学学业不良儿童在多项工作记忆任务(分别涉及数字信息加工和句子加工)上成绩低于对照组, 他认为数学学业不良儿童存在工作记忆的广泛损害。同时, Passolunghi和 Siegel(2004), Passolunghi, Vercelloni和 Schadee (2007)在2001年研究的基础上, 进一步跟踪了数学学业不良的儿童在一年来的发展变化, 结果显示：数学学业不良儿童仍然在工作记忆上具有广泛的缺损。但是, 这些儿童在言语速度以及计数速度的任务上并没有表现出异常, 这些任务都涉及到语音环路的功能。在 Keeler和 Swanson (2001)的研究中也指出,学习困难儿童解决数学应用题的正确率与语音加工和言语工作记忆成绩均有显著相关; 言语工作记忆和视－空工作记忆能力均是数学困难儿童数学成绩的重要预测因子。此外, Swanson和Sachse-Lee(2001)以数学学业不良儿童为被试探讨了工作记忆所包含的两个附属系统和解决数学学习任务能力之间的关系, 结果发现：数学学业不良儿童在应用题解决的准确性、语音加工、一般领域的工作记忆和言语工作记忆等方面都劣于同龄儿童; 言语和视－空工作记忆是独立于语音加工之外, 对解题准确性有重要影响的变量。这一结论说明了工作记忆两个从属系统是导致数学学业不良的明显因素。在上世纪90年代的研究(Cornoldi, Vecchia, & Tressoldi,1995; McLean & Hitch, 1999)中较为一致的结论认为, 数学学业不良儿童视－空工作记忆受损而语音环路正常, 并特别强调视－空工作记忆在数学活动中的重要性。但对这一问题的近期研究则表现出了不同的观点。Kathleen和Swanson (2001)认为, 数学学业不良既与视觉－空间工作记忆广度有关又与言语工作记忆广度有关, 而且, 他们认为数学计算更多依赖的是言语工作记忆, 而不是视觉－空间工作记忆。

国内也有一些学者在工作记忆对数学学业的作用问题上产生了一些重要的研究观点。如, 王恩国、赵国祥、刘昌、吕勇和沈德立(2008)认为数学学业不良在计算广度上的缺损主要是由于语音环路的影响, 而语文困难的视空间工作记忆是完好的。刘昌(2004)研究了数学学业不良儿童的认知加工机制。他认为数学学业不良几乎完全是由于数字工作记忆能力下降引起的, 而与空间工作记忆能力下降无关, 而由数字工作记忆下降引起数学学业不良的更深层次原因可能在于较差的语音加工速度与中央执行功能二者的共同影响。宋广文、何文广和孔伟(2011)将小学生应用题难度进行分类, 研究发现语音环路只影响高难度数学应用题, 而视觉－空间模板对低、中、高难度的数学应用题解决都具有重要影响。俞国良和曾盼盼(2002)对数学学习不良儿童视觉－空间表征与数学问题解决进行研究时发现, 数学学业不良儿童和一般儿童使用视觉－空间表征策略的程度没有显著差异, 但数学学业不良儿童的解题正确率以及使用图式表征策略的程度显著低于一般儿童, 使用图像表征策略的程度则显著高于一般儿童。在解题正确率和图式表征策略这两个变量上, 数学学业不良儿童和一般儿童的年级发展趋势是相同的, 都随年级的升高而提高, 而且转折点似乎发生在四、五年级之间。但是, 在图像表征策略的使用上, 两类儿童的年级发展趋势却不相同, 一般儿童使用图像表征策略的程度有随年级的升高而下降的趋势。数学学业不良儿童和一般儿童的空间视觉化能力都随年级的升高而提高, 两类儿童之间该能力没有显著差异。张明和隋洁(2003)对分散注意条件下探讨学习困难和优秀的学生, 两者比较研究发现, 在不同干扰条件下, 学习困难学生视觉－空间工作记忆均比优秀学生差; 干扰任务不仅影响学习困难学生的视觉－空间工作记忆加工能力, 也影响他们的存储能力。这说明数学学业不良学生不能有效抑制外界干扰可能是他们视觉－空间工作记忆存在缺陷, 这是导致数学困难的主要原因之一。视－空间工作记忆有缺陷是各类学习困难学生普遍存在的问题。

综上所述, 研究都认可视觉－空间模板和语音环路的作用, 但两者分别对哪一类数学学业不良学生有预测作用, 是否数学学业不良是两者的共同作用, 目前尚无定论。主要的三种观点是：第一, 语音环路与视－空模板两个系统均存在缺损; 第二,语言环路具有缺损而视－空模板正常; 以及第三,视－空模板缺损但语音环路没有发现异常。

总体而言, 虽然数学学业不良领域已有较多研究者关注, 也有大量研究探讨了工作记忆与数学学习之间的关系。但可能由于目前数学学业不良的筛选与分类标准不统一, 因此, 数学学业不良的核心缺损模式至今仍尚无定论。本研究针对目前所面临的争论焦点, 将进一步以 Baddeley工作记忆模型作为主要的认知理论模型, 将数学学习根据课程内容的不同领域进行划分, 系统探讨伴有特定内容领域的数学学业不良初中生的认知行为特点及发展规律, 突出工作记忆在初中数学学业中的特异性表现机制。全文包括两个研究：

研究一：探讨数学学业不良初中学生的特异性工作记忆的发展模式。研究将筛选数学学业不良学生作为实验组, 并选取智力、年龄、性别等相匹配的初中生作为对照组。根据国家数学课程标准, 将数学学习分为数与代数、空间与几何两大类, 分别探讨具体内容领域数学学习的认知加工机制。由于数学学业不良涉及面广, 类型多样, 但很少有研究以特异性课程内容作为划分依据来分类具体的数学学业不良类型。以往笼统的划分可能也是造成数学学业不良在工作记忆等认知过程缺损模式的特征问题上产生争论的一个原因。

研究二：在空间与几何领域, 进一步选取初一学生具体的数学学习任务——轴对称与中心对称图形。探讨在解决具体课堂教学知识点时所涉及到的工作记忆加工成分。这一研究将为研究一代数与几何学习的工作记忆特征在一定程度上进一步提供支持证据。

2 研究一工作记忆在初中代数与几何任务中的特异性表现

2.1 研究目的

由于代数和几何学习可能涉及不同的认知加工过程, 下面的研究将把数学学习进一步分类为数与代数学习, 空间与几何学习, 探讨工作记忆的三成分对这两类学校最常见的数学任务解决过程的影响。研究所要探究的主要目的是：工作记忆各成分在数学学习中扮演的角色是具有领域普遍性还是特异性。如果工作记忆多重成分对各类数学任务均具有明显作用, 那就表现出普遍性特征; 如果工作记忆各成分对各类数学任务的作用不一致, 那各个成分就可能具有领域特异性特征。

2.2 研究过程

2.2.1 被试筛选

被试来自上海普通中学预初年级(六年级)、初一(七年级)、初二(八年级)学生。全体学生参加数学标准化测验, 每次测验为60分钟。并且收集最近三次期中、期末数学考试成绩, 将成绩转换为标准分数。

实验组的筛选条件为：数学标准化测验的标准分位于最后20%, 并且学校最近三次期中、期末考试成绩标准分低于 20%, 两者同时符合条件的学生。

对照组的筛选条件为：数学标准化测验的标准分处于最高的20%, 并且学校最近三次期中、期末考试成绩标准分处于最高的20%, 两者同时符合条件的学生。

排除标准：根据学习动机诊断测验(MAAT), 排除学习动机低于2个标准差的学生。同时, 为了排除智力缺陷的学生, 首先根据班主任、数学任课教师日常观察推荐, 再结合瑞文高级渐进矩阵测试,排除智商分数处于80以下的学生。

最后共筛选两组学生111名, 其中数学学业不良学生 55名, 为实验组; 数学优秀组学生 56名,为控制组。男生48名, 女生63名。平均年龄11.97岁。被试情况见表1。

表1 被试情况表

2.2.2 数学学业成绩

数学学业成绩为标准化数学测验分数和学校近三次期中、期末考试成绩的平均分。代数成绩的计算方法如下：逐题分析数学标准化测验题册内的题目, 根据《国家数学课程标准》(2003)划分数与代数领域的依据, 逐条对照知识点双向细目表。计算每位学生在数学标准化测验中代数题答对正确数。几何成绩计算方法同代数。统计与概率部分在此研究中不作为单独的内容领域分类探讨。

2.2.3 工作记忆成绩

工作记忆包含三个成分,每个成分设计两个实验任务, 实验程序采用E-prime 1.1程序编制, 测试在Pentium 4计算机上单独完成(CPU 1500 MHz)。6个实验任务简述如下：

信号停止任务(Stop-signal), 测查中央执行系统功能。信号停止任务研究借鉴 Logan和 Cowan(1984)经典的任务范式, 刺激信号采用“×”和“÷”两个数学符号, 反应刺激在屏幕上停留的最长时间是2000 ms。在信号停止任务中, 在部分反应刺激出现之后的一小段时间间隔, 会出现一个停止刺激的信号, 反应刺激与停止刺激间的时间间隔被称为SOA (Stimulus Onset Asymmetry)。在 SOA 之后, 可能会出现“嘟”的声音, 这是一个停止信号。本实验设置了5个不同的SOA条件, 分别为SOA为10 ms(简称 SOA10)、70 ms (简称 SOA70)、150 ms (简称SOA150)、230 ms (简称 SOA230)、300 ms (简称SOA300)。信号停止任务练习阶段有停止信号的 5次, 每个SOA条件各出现一次。正式测试阶段全部被试需要接受反应200次, 两种刺激信号各100次。其中有停止信号的50次, 每种SOA的条件下各10次, 两种符号各占50%。

Flanker任务, 测查中央执行系统功能。其中刺激情况(有无靶刺激和干扰情况)条件为组内变量,组别与年级类别为组间变量。有无靶子刺激条件有两个水平：有靶子刺激和没有靶子刺激。干扰情况有三种：两侧有干扰、两侧无干扰以及中性刺激。因变量为被试反应的正确数及其反应时。选取数字符号“5”作为靶子刺激, 其它数字为干扰刺激。根据有无靶子刺激以及干扰情况的匹配, 共有6种刺激情况。所有的刺激都呈现于一个浅绿色的23 cm ×17 cm的长方形背景框的中央。在每一个刺激呈现之前, 背景框中都会出现一个2 cm × 2 cm大小的“＋”号, 提醒被试目标刺激即将出现, “＋”提醒刺激停留的时间长度为200 ms。目标刺激呈现的时间200 ms。从目标刺激呈现开始, 被试就可以作出反应, 被试需要在 1500 ms内作出反应, 其中前 200 ms是有刺激呈现的状态, 后1300 ms是没有刺激呈现的。被试反应后则等待下一次的“＋”出现。Flanker任务练习阶段包括所有6种刺激情况, 每种情况各出现3次, 总共有18次。正式测试阶段反应共288次。靶子与非靶子各占50%。有干扰的情况有120次, 中性的情况也是120次(非靶中性96次,非靶干扰24次, 靶子中性24, 靶子干扰96次), 无干扰的情况(单个刺激)是48次。最后将这6种情况反映正确率转换成标准分, 其平均值即作为Flanker任务的成绩。

N-back任务, 测查视觉－空间模板。任务条件具有三个水平, 分别是0-back、1-back和2-back, 采取被试内设计; 组别和年级是被试间变量。施测的材料选取三角形、圆形和正方形三种实心的黑色几何图形。在0-back的任务中, 被试只要对刺激图形作出选择性反应即可。在实验中, 要求被试一看到三角形就按 L键, 其余的图形(包括圆形和正方形)都按A键。在1-back任务中, 要求被试对当前看到的图形与上一个作比较, 判断是否一致。在2-back任务中, 要求被试对当前看到的图形与上二个(前面再前面一个)图形比较, 判断是否一致。图形刺激呈现500 ms, 被试的判断时间有2000 ms。

九格图形空间位置任务, 测查视觉－空间模板。任务难度有二个水平, 简单空间任务和复杂空间任务。测验的材料是3×3 九格图, 简单空间任务只在九格图中出现图形刺激 “○”, 它本身不具有空间信息, 只在九格图中的不同位置产生空间信息;复杂空间任务刺激图形包括“＜”、“＞”、“《”、“》”、“≤”以及“≥”等符号, 这些符号不仅在九格图中不同位置产生空间信息, 它们本身还具有左右的方位信息, 以此加大了空间工作记忆的负荷。在计算机白色屏幕上呈现 3×3九格图, 在简单空间任务中, 被试需要判断先后出现在九格图中的刺激“○”是否在同一个位置, 随着难度的加大, 刺激的个数逐渐增多, 最简单的是一个刺激, 最多有 6个刺激。在复杂空间任务中, 被试不仅要判断先后出现在九格图中的刺激是否在同一位置, 而且要判断先后的图形是否完全一致。先后两次刺激呈现时间都是 1000 ms, 目标刺激和反应刺激中间插入500 ms屏蔽刺激, 为一个空白的九格图。被试在第二次反应刺激呈现后即可作出判断, 在反应刺激呈现1000 ms消失后, 被试仍有2000 ms的时间作出反应。计算机记录被试的判断以及反应时间。

数字广度, 测查语音环路。主试与被试一对一口头测试的方式, 主试以每秒2个数字的速度大声朗读数字, 每组数字的长度是 2～8个, 学生的任务在听完主试报数后, 将所听到的数字倒过来复述。

句子广度, 测查语音环路。任务根据Daneman和Carpenter (1980)经典的阅读广度任务改变。屏幕上呈现一句句子, 句子通常包含5～9个汉字。例如：“北京是中国首都”。每句句子的最后一个名词为目标刺激, 即要求被试记住每句句子的最后一个词语,如“首都”。与此同时, 要求被试5秒内判断此句句子逻辑是否正确, 并作出按键。呈现完一定数量的句子后, 屏幕中出现“？？？”作为回忆线索, 让被试回忆目标刺激并出声报告。随着难度加大, 呈现句子的数量会逐渐增多, 至少是 2句句子, 即句子广度为2, 最多广度为7。在操作过程中, 被试在接受指导语后进入练习阶段, 共有3组广度为2的句子。练习结束后, 主试根据被试练习的正确率来判断被试是否真正明白指导语, 再进入正式测试阶段。正式实验时, 主试在记录表上记录被试的反应,但不记录判断正确率。报告完之后按任意键进入下一组测试。

选取各实验任务的指标的平均值, 计算该项任务的得分。再将实验组和对照组的原始分转换为

分数。由于实验组和对照组在任务表现中分布可能是“双峰分布”而非呈现标准正态分布。在计算标准

分数时, 不能将两组学生的成绩简单混合计算。因此, 首先计算对照组学生在各项敏感性指标的正态分布

分数, 据此分布的平均数和标准差计算实验组各项指标的Z分数(蔡丹, 2010)。

2.3 研究结果

2.3.1 两组学生在工作记忆各任务中的表现

比较实验组与对照组学生在6个工作记忆任务中的表现(表 2)。结果发现在测查中央执行系统的信号停止任务, 测查视觉-空间模板的 N-back任务, 以及测查语音环路的句子广度和数字广度任务中, 两组学生的表现具有极其显著的差异。说明与对照组相比, 实验组学生在工作记忆中三个成分均存在一定程度的缺损。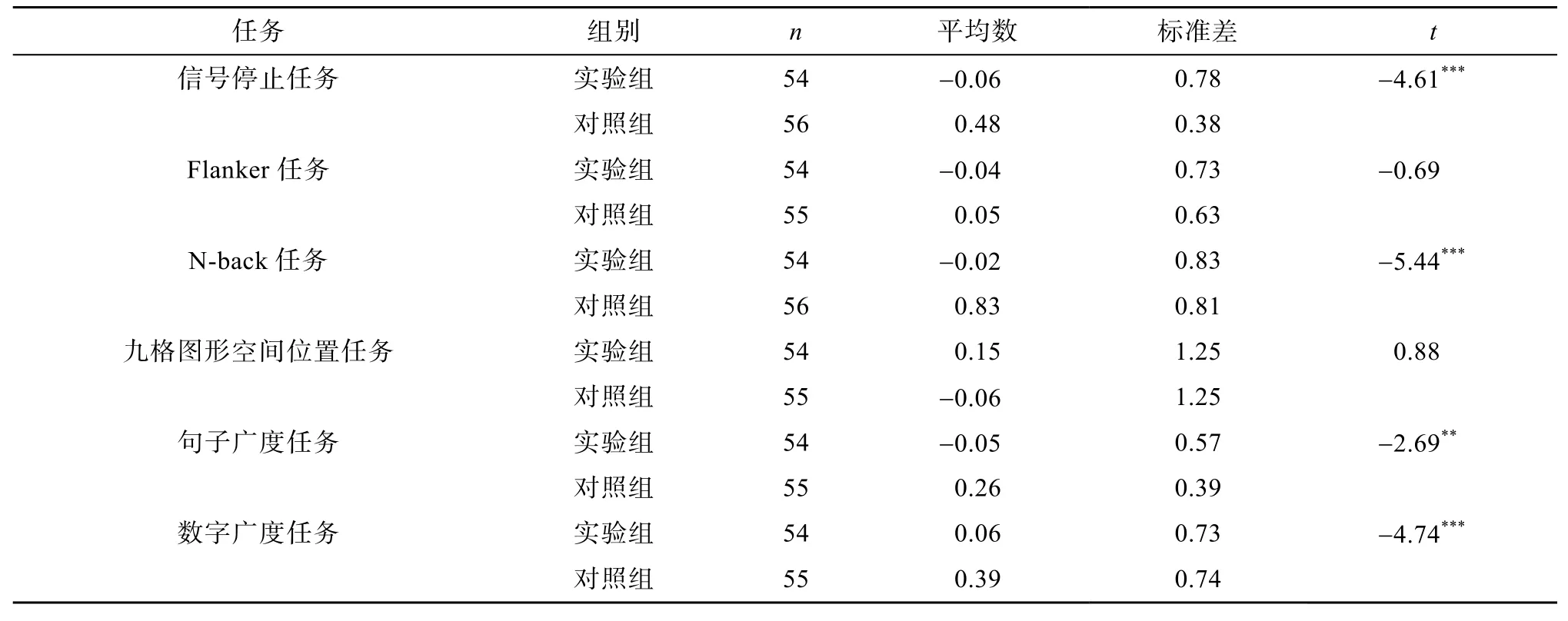

表2 两组学生工作记忆成绩比较

2.3.2 工作记忆在各类数学学习中的作用

分别就数学总分、数与代数、空间与几何三个部分, 分别探讨工作记忆与各种数学学习类型的关系。(1)

数学总分与工作记忆的关系

采用Stepwise逐步回归法, 分别用工作记忆6个任务指标预测全体学生以及预初、初一、初二年级学生的数学标准化成绩(表3)。

回归分析显示, 有三项任务对初中生数学学业成绩预测显著, 分别是N-back任务、数字广度任务和信号停止任务。这三项任务分别属于视觉－空间模板、语音环路和中央执行系统。这提示着, 工作记忆各成分对初中生数学学业成绩均起到重要的影响作用。三项任务总共能解释41%数学成绩的变异。对预初年级学生而言, 同样有三项任务预测了数学学业总分, 分别是数字广度任务、信号停止任务以及 N-back任务。这三项任务同样各自属于工作记忆的三个成分, 预初年级与初中全体学生的工作记忆机制作用不同的是, 三项任务预测的重要性程度发生变化：视觉－空间模板的地位在预初年级略有下降。但是, 这三项指标的共同的解释力度较高, 总共有 51%的解释能力。对初一学生而言, 分别有 N-back任务、信号停止任务以及句子广度任务进入了回归方程。这三项任务同样分别属于视觉－空间模板、中央执行系统以及语音环路三个成分。上述三项指标解释初一数学学业成绩的作用效果非常好, 达到 59%的解释力度。对初二学生而言, 只有N-back一项任务进入回归方程。也就是说,初二学生的数学学业成绩最重要的是视觉－空间模板的参与。单个因子的预测能力达到21%。其余两个工作记忆成分均不显著。

表3 工作记忆各指标对初中生数学总分影响的逐步回归分析

(2)

空间几何学习与工作记忆的关系

采用Stepwise多元逐步回归方法, 分别将工作记忆6个任务指标预测全体学生以及预初、初一、初二年级学生的几何学习成绩(表4)。

回归分析显示, 有两项任务对初中生几何学习成绩预测显著, 分别是N-back和信号停止任务。这两项任务分别是视觉－空间模板以及中央执行系统的任务。这提示初中几何成绩主要受到视－空工作记忆以及中央执行系统的影响, 而没有语音环路的作用。两项指标能解释20%几何学习成绩。对于预初年级的几何学习, 只有 N-back一项任务进入了回归方程, 也就是说, 只有视觉－空间模板能对预初年级的几何学习起关键影响作用, 该因子单独预测力达到28%。对于初一的几何学习, 和全体学生一样, 有 N-back和信号停止任务两项指标预测了几何成绩, 这同样属于视－空模板以及中央执行系统的作用, 它们两项能解释 37%几何学习的变差。初二的几何学习并没有任务进入回归方程, 在本实验中没有特别的因子对初二几何学习起到重要预测作用。所有年级的几何学习均没有显示出语音环路的显著作用。

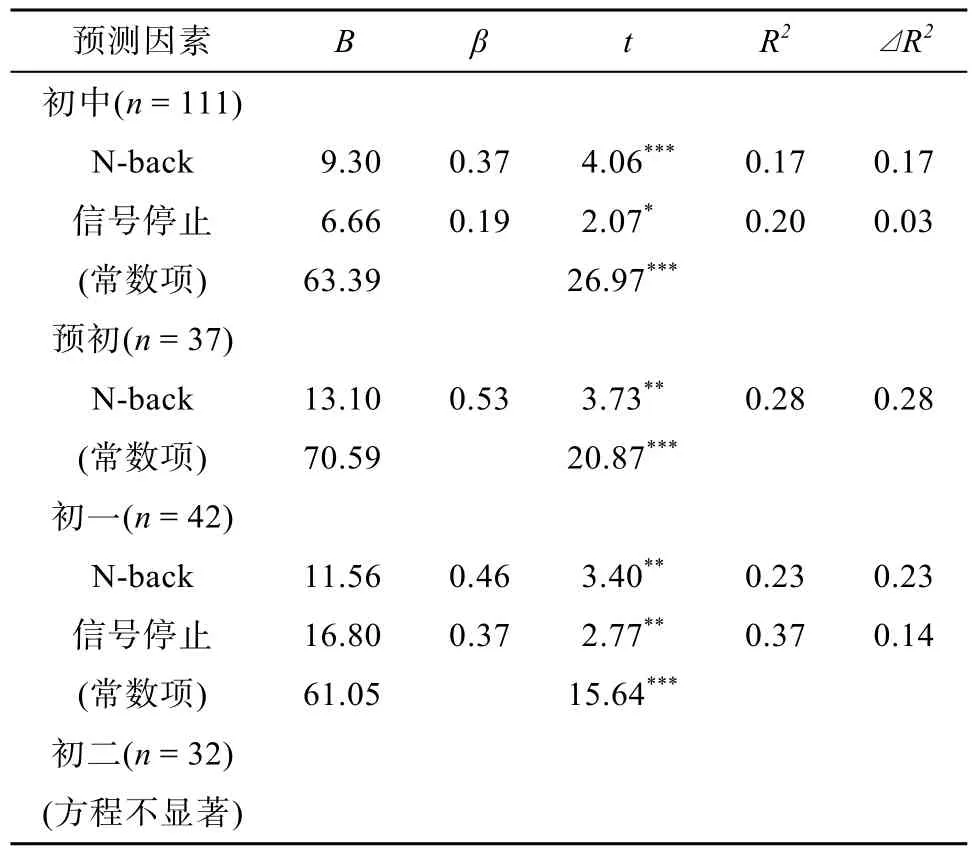
表4 工作记忆各指标对初中生几何成绩影响的逐步回归分析

(3)

代数学习与工作记忆的关系

采用同样的Stepwise多元逐步回归方法, 将工作记忆6个任务指标预测全体学生以及预初、初一、初二年级学生的代数学习成绩(表5)。

表5 工作记忆各指标对初中生代数成绩影响的逐步回归分析

工作记忆对代数学习影响的回归分析结果显示, 有三项指标对初中生代数成绩预测显著。它们是数字广度任务、N-back任务以及信号停止任务。这三项任务分别是语音环路、视觉－空间模板以及中央执行系统的指标。说明初中代数学习需要工作记忆各个成分的参与。然而, 与初中数学总成绩所不同的是, 语音环路第一个进入了代数学习的回归方程, 并且单个因素的

变化率达到17%, 也就是说, 语音环路在代数学习中的作用比综合数学学习更显著。预初年级学生的代数学习有两项指标进入回归方程, 分别是数字广度和信号停止任务。这是语音环路和中央执行系统的任务。两项指标共同解释的

达到 40%。初一学生的代数学习有三项指标进入回归方程, 分别是信号停止任务、N-back任务以及句子广度任务, 这三项同样涉及到工作记忆的三个成分。而这三项指标对初一代数影响非常大,累积能够解释66%的代数成绩方差变异。初二学生只有一项指标显著预测了代数学习, 即 N-back任务, 主要是视觉－空间模板的作用。单个因子解释率为14%。

视觉－空间模板以及语音环路是否确实在初中空间几何任务中具有普遍性及特异性的双重功能, 研究二将选取初一学生具体的学习任务, 进一步求证这一结论。

3 研究二工作记忆在初一年级轴对称与中心对称空间任务中的特异性表现

3.1 研究目的

图形的轴对称和中心对称是《国家数学课程标准》(2003) (以下简称课标)中规定初一学生所需掌握的知识点, 这一知识点的分类属于空间与几何的领域。这一部分所选取的研究对象是尚未正式接受“轴对称和中心对称图形”这一知识点课堂教学的学生。实验中先根据课标所要求的教学目标, 对他们当堂讲解轴对称和中心对称图形的知识点, 讲解完毕后立即对学生掌握情况进行测试。研究目的是证实初一学生在解决某一具体空间与几何学业知识点时, 是否同样符合研究一所得到的视觉－空间模板以及语音环路在空间几何任务中具有普遍性及特异性的双重功能。

3.2 研究方法

3.2.1 被试筛选

参与研究一的全体初一年级学生, 共42名。由于1名学生未完成全部测试, 有效被试共 41名。其中数学学业不良组(实验组)学生22名; 数学优秀组(对照组)学生19名。男生12名,女生29名。平均年龄149.9个月(约12岁6个月)。

3.2.2 测试工具轴对称与中心图形任务成绩：

“图形的轴对称与中心对称”这一知识点是国家数学新课标以及上海市初一数学教学大纲中要求学生在初一掌握的知识点。测试任务采用自编的轴对称和中心对称测试。测试共分A/B两套, 两套测试内容一致,题目顺序安排不一样。以免被试之间交流。

本实验分为知识点讲解, 例题讲解和正式测试三个部分。正式测试一共有42个图形, 答题时间为15分钟。答题结束后收集题本, 并发送小礼物。

统计每名被试在轴对称图形和中心对称图形两部分任务中的答对数(击中), 以及答错数(虚惊,不是对称图形认为是对称图形)。答对数减去答错数为该任务的得分。

工作记忆成绩：

同研究一。

3.3 研究结果

3.3.1 两组学生在轴对称与中心对称任务得分的比较

分别比较实验组和对照组学生在轴对称图形任务中的答对数、答错数以及总分(表6)。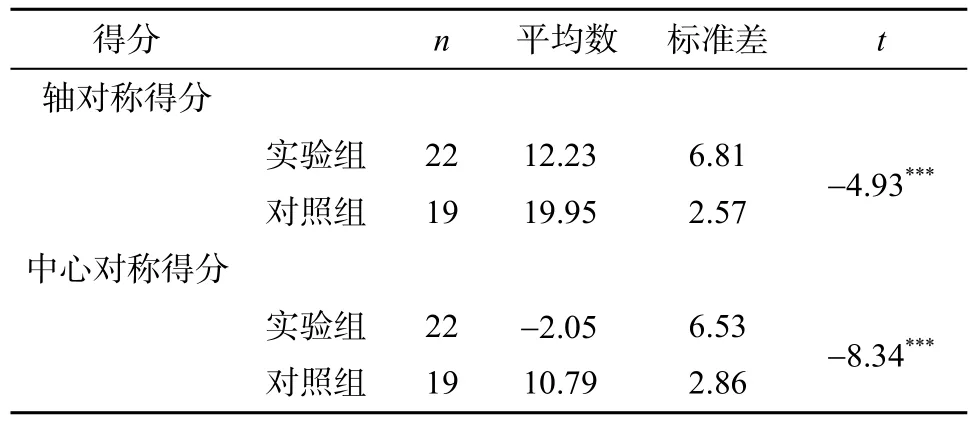

表6 两组学生轴对称图形得分比较

结果表明, 实验组学生和对照组学生在轴对称图形测试中的成绩无论是答对数(

=−3.97,

＜0.001)、答错数(

=3.76,

＜0.01)以及总分(表 6)都具有极其显著的差异。实验组学生和对照组学生在中心对称图形测试中的成绩无论是答对数(

=−6.59,

＜0.001)、答错数(

=4.85,

＜0.001)以及总分(表 6)都具有极其显著的差异。实验组答对数和总分明显低于对照组, 而答错数明显多于对照组。

3.3.2 轴对称与中心对称图形任务与工作记忆的关系

我县其中部分的建筑保留60、70年代的建筑。其中局部新建新式的建筑呈点状布置。个别的住户也对建筑的局部也进行了加固改造，整个村落的建筑形式以砖混形式为主，木质结构的建筑现在已不满足居民需求，在不久将逐步改造维修。随着生活水平的提高，现状的住户环境仍然需要提高，公共设施需要改善，村貌需要整体的协调型设计。

(1)

轴对称图形任务与工作记忆的关系

采用Stepwise逐步回归法, 将上述6个工作记忆任务衡量指标作为自变量, 轴对称得分作为预测变量, 分析轴对称图形与工作记忆的关系(表7)。

回归分析显示, 有二项任务对初一学生轴对称图形的成绩具有显著预测作用, 它们是信号停止任务和N-back任务。这两项任务中, 前者是中央执行系统测查任务, 后者视觉－空间模板任务。这提示着, 工作记忆三个成分中, 中央执行系统以及视觉－空间模板对轴对称的成绩起到重要的影响作用。这二项任务总共能解释 29%轴对称图形成绩的变差。语音环路对轴对称图形的预测作用不明显。

表7 工作记忆任务对轴对称图形得分影响的回归分析

(2)

中心对称图形任务与工作记忆的关系

采用Stepwise逐步回归法, 将6个工作记忆指标作为自变量, 中心对称得分作为预测变量, 分析中心对称图形任务的成绩与工作记忆的关系(表8)。

表8 工作记忆任务对中心对称图形得分影响的回归分析

回归分析显示, 有二项任务对初一学生中心对称图形的成绩具有显著预测作用, 它们是 N-back任务和信号停止任务。这二项任务中, 前项任务是视觉－空间模板的测查任务, 后项任务是中央执行系统任务。这提示着, 工作记忆三个成分中, 视觉－空间模板以及中央执行系统对中心对称的成绩起到重要的影响作用。这二项任务总共能解释59%中心对称图形成绩的变差。语音环路系统对中心对称图形的预测作用不明显。

4 讨论

4.1 中央执行系统在数学学习中具有领域普遍性作用

研究分为两部分考察了各类数学学习的工作记忆作用机制。总体而言, 研究结果从实证角度上支持了工作记忆各个成分对数学学习有着彼此不同的作用。

研究结果显示, 中央执行系统对初中总体的数学学习(包括代数和几何)均起到重要作用, 这提示中央执行系统的作用机制具有领域普遍性。研究二中发现中央执行系统对轴对称和中心对称图形任务有重要的作用。结果支持了中央执行系统在数学学习任务中的领域普遍性作用的假设(Andersson &Lyxell, 2007; St Clair-Thompson, 2011; McLean &Hitch, 1999; Passolunghi & Siegel, 2001, 2004;Swanson & Beebe-Frankenberger, 2004; )。

结果显示, 信号停止任务是中央执行系统对数学学习影响的敏感指标。信号停止任务主要是考察学生加工速度以及抑制控制的能力。也就是说, 潜在的加工速度和抑制控制对数学学习各个领域均有着重要作用。抑制过程的缺陷会对数学问题解决带来很多阻碍。Passolunghi和 Siegel(2001)对数学学业不良和优秀的学生进行比较发现, 数学学业不良学生工作记忆的缺陷主要在于抑制控制能力, 他们无法忽视与解题无关的信息而继续保持相关信息的操作。数学学业不良的学生容易在工作记忆任务上表现出更多无意识的冲动错误, 他们在解决问题的过程当中, 无法长时间从事相关活动而压制分散信息。蔡丹、李其维和邓赐平(2010)也提出, 工作记忆的个体差异本质在于中央执行系统的作用, 而中央执行系统核心就是注意控制能力。

分别考察轴对称图形以及中心对称图形两组的差异, 可以发现初一两组学生在中心对称图形的差异比轴对称图形更大。这可能是由于轴对称主要是翻折产生重合, 中心对称是围绕一个中心旋转180度产生重合, 中心对称任务需要更多的空间想象能力。根据几何思维发展的特点, 直观性水平是学生几何学习最初的概念形式(徐速, 2006), 学生根据几何图形的外表形状来确认和操作几何对象。这同样符合在轴对称的任务上, 学生只要将图形一分为二, 如果另一半的图形在外表上与另一半一样,只是位置相反, 就可以判断为轴对称图形。然而在中心对称图形中, 学生无法在平面中直接判断, 必须有一个旋转的过程, 心理旋转需要较多空间工作记忆的负荷(Hyun & Luck, 2007)。因此, 所需负荷较少的轴对称图形任务相对会比中心对称任务更简单, 两组学生的个体表现差异也会更小。

中央执行系统的缺损对各领域数学学习的影响还表现在无法将已有的知识基础整合到现有的信息中去, 这是语义记忆信息提取的困难(Gathercole & Pickering, 2000; Monette, Bigras, &Guay, 2011; Swanson & Beebe-Frankenberger, 2004)。这些个体很难在上课的时候进行加工与存储并行的操作, 这需要较高的工作记忆要求。因此, 当个体处于中央执行系统能力缺陷时, 他将面临数学学习成绩提高的认知瓶颈, 今后对中央执行系统功能的提高开展干预和补救是十分必要的, 否则数学学业不良学生难以在课堂上高效地完成老师所要求的数学任务。

4.2 视觉－空间模板和语音环路系统在数学学习中的特殊作用

研究结果显示, 视觉－空间模板在数学学习中的作用非常重要, 无论在数学总成绩, 还是在几何、代数领域均表现出普遍的意义, 并且在空间与几何任务中的作用比代数部分更显著(Andersson &Lyxell, 2007; McLean & Hitch, 1999; 王恩国等,2008)。从结果来看, 视觉－空间模板对初中三个年级的数学总分、几何成绩和代数成绩预测均非常显著, 这个结果支持了视觉－空间工作记忆在数学学习发挥着领域普遍性的观点, 它与各类数学学习均有着密切关系(McLean & Hitch, 1999)。而不支持研究者认为数学学业不良与视－空间工作记忆能力下降无关的结论(Wilson & Swanson, 2001; 刘昌,2004)。这一结果在研究二对初一轴对称和中心对称图形任务的研究中同样得到证实。

结果发现, N-back任务是视-空模板对数学学习影响的敏感指标。Reuhkala (2001)认为, 视觉－空间工作记忆涉及静态与动态两种能力, 静态的视－空能力主要可以通过工作记忆的双任务范式加以衡量, 在本实验中所采用的 N-back任务以及九格图形空间位置任务都属于静态的视－空能力。这也与 Owen, McMillan, Laird和 Bullmore (2005)对N-back任务的元分析研究结果一致, 以 N-back任务作为工作记忆测查工具的研究越来越多, 通过改变刺激材料, 可以获取在线的视觉－空间工作记忆信息, 也可以获取言语听觉工作记忆信息。N-back任务用于考察数学学习困难学生的认知缺损机制具有如下几个优势在于：首先, N-back任务受到更少混杂信息干扰, 能较纯净地要求个体保持工作记忆信息; 其次, n个任务允许系统操纵工作记忆负荷, 由于工作记忆负荷的改变, 导致数困生表现成绩的变化, 所产生的差异可解释为工作记忆负荷高低的特殊加工作用。本研究中, 2-back任务所需的空间负荷较1-back任务大, 任务更难, 被试需要在呈现当前图形时, 首先提取前二个图形与之匹配,与此同时, 还必须记住当前图形刺激和上一个图形刺激, 以备下一个和再下一个刺激呈现时提取出来与这两个进行比较。因此, 对于数学学习困难学生而言, 在高负荷条件下, 表现出工作记忆的能力的相对不足。研究证明了在一般情况下, 个体工作记忆的高低并不能表现在完成一般任务的好坏上(如,本实验中的0-back), 但是如果对任务进行干扰, 或者加大操作任务所需的工作记忆负荷量, 那么工作记忆能力高的个体便能表现出很好的对抗干扰能力, 从而更好完成任务。

本研究发现语音环路只在代数和综合数学中显示出重要作用, 而在几何学习成绩中作用不明显,支持了语音环路在数学任务中的领域特殊性的作用(Passolunghi & Siegel, 2004; Simmons et al., 2012;Zheng, Swanson, & Marcoulides, 2011; Wilson &Swanson, 2001)。具体考察语音环路对各年级各数学任务的作用发现：在初中三个年级的数学总成绩以及代数成绩中, 语音环路作用显著, 在预初和初一年级的数学总分和代数成绩中, 语音环路也具有重要地位。但是, 在几何成绩中, 任何一个年级均没有显现语音环路的作用。这表明, 语音环路对数学学习的影响主要通过数与代数产生作用, 而不是在各个领域均体现优势。在比较语音环路对代数和数学总分影响作用时也可以发现, 语音环路在代数成绩中的影响力更高。具体体现在代数学习中, 语音环路任务在初中总成绩和预初年级的代数成绩中均第一位进入回归方程, 而在数学综合成绩中只有预初年级的语音环路第一位进入回归方程。此外,在比较了代数和几何的作用机制后发现, 尽管视觉－空间工作记忆在两种数学内容领域中均起到重要作用, 然而, 当语音环路系统在数与代数部分起作用后, 视觉－空间模板的作用略显下降。表现在空间与几何任务中, N-back任务作为视－空模板几乎都第一位进入回归方程, 解释的方差变异量也较高。而在数与代数任务上, 语音环路系统在初中全年级和预初年级的代数成绩中首个进入回归方程,具有最大的解释力, 视－空模板任务的相对解释力下降。这一结果从另一个侧面证明了语音环路在数学学习中的领域特殊性功能, 支持了前人结论(Passolunghi & Siegel, 2004; Wilson & Swanson,2001; Zheng et al., 2011)。Passolunghi和 Siegel研究了数学学业不良的学生, 尽管他们在中央执行系统中的缺损具有普遍性, 但是在涉及语音环路系统的言语速度和计数速度等数学任务中, 没有发现语音环路功能的缺损。

研究证实了视－空工作记忆是独立于语音环路和中央执行系统而单独起作用的一个领域普遍性成分(Krajewski & Schneider, 2009; Reuhkala,2001)。由于视－空工作记忆的缺陷, 导致了学生暂时存储与数学有关的视－空信息受到局限, 数学学业不良的学生没有更多的“空间”收集数学任务中的细节特征。因此, 视觉－空间模板会在几何学习、代数学习中均起到重要的作用。语音环路在数学学习中的作用机制一直受到研究者激烈的讨论, 通过本研究的实证探讨, 结果支持语音环路在代数学习中确占有一席之地(刘昌, 2004)。正如研究者Kathleen和Swanson (2001)认为的, 数学学业不良既与视觉－空间工作记忆广度有关又与言语工作记忆广度有关, 但是关于数学计算的缺陷更多是由于言语工作记忆。然而, 随着任务性质和要求的不同, 语音环路所起的作用也具有特殊性, 其作用主要体现在数与代数的学习部分, 而对空间与几何学习影响不显著。语音环路的受损将直接导致学生无法将数学信息通过语音记忆传输到高级处理水平。执行系统的作用是将当前的语音信息融合到已有的字词、数字知识中, 语音环路的工作是进一步对这些信息进行分析并存储在语音短时记忆中, 以便及时腾出必要的资源给下一个信息占用。由于空间与几何任务更难以将内容转换为语音信息, 更重要的是视觉与空间能力的实现, 因此语音工作记忆对几何任务的影响就不明显了。

4.3 不同年级初中生数学学习的工作记忆特点

在各个年级由于数学任务要求的不同, 对工作记忆也会有着不同的要求。研究分析了数学学习在三个年级的工作记忆作用机制的区别后发现, 预初年级学生数学学习的工作记忆要求从高到低依次是：语音环路系统、中央执行系统、视觉－空间模板; 初一数学学习的工作记忆要求依次是：视觉－空间模板、中央执行系统和语音环路; 初二只发现视觉－空间模板在数学学习中起到重要作用。从数学成绩影响因素结果中, 我们可以推断数学任务随着年级的增高, 视觉－空间模板的作用会逐步突显出来, 语音环路的作用会逐渐降低。这一结果在考察代数学习成绩所需的工作记忆特点中得到再次验证, 在预初年级代数学习中, 语音环路起最重要的预测作用, 中央执行系统其次。到了初一的代数学习, 视觉－空间模板的作用上升到第二位, 而语音环路的作用下降至第三位。到了初二的代数学习,只有视觉－空间模板的 N-back任务单独产生显著的预测作用。结果说明初中不同年级数学学习具有不同的认知要求, 从另一侧面也可以推断, 工作记忆各系统在初中发展的成熟度, 将直接影响数学学习成绩。在分析语音环路在数学学习中的具体作用后将不难理解年龄越高, 需要语音工作记忆参与的成分相对降低的结论。研究证明, 语音环路在数学计算、心算等基础数学任务中具有重要作用(Fürst& Hitch, 2000; Simmons et al., 2012), 或者在阅读或理解数学题目时发挥作用(Passolunghi et al.,2007), 这些能力主要在低年级学生的数学学习中显得比较重要, 语音工作记忆的缺陷将导致学生一边计算一边遗忘的情况, 从而抑制了学生有效地解答数学题目。研究也证实了在低年级数学任务中,语音复述占据了大量的语音工作记忆容量, 而高年级在完成数学题目时, 计算、心算等这些基础能力已经较少占据工作记忆资源, 因此随着年龄逐渐提高, 语音环路的作用可能会随着数学任务的要求而逐渐降低(Meyer et al., 2010; Krajewski & Schneider,2009)。相反随着年级的提高, 数学题目更需要抽象的空间加工能力, 因此, 视觉－空间模板的作用就更为明显了。

5 结论

工作记忆在数学学习中总体表现出领域普遍性特征, 但三个成分在不同年级的数学任务中有独特的作用。

首先, 中央执行功能总体在初中生数学学习中表现出普遍性的作用机制, 数学学习困难的学生在中央执行系统中的缺损也尤为明显。

其次, 视觉－空间模板在综合数学、数与代数、空间与几何等内容上均表现出积极的作用。相比较代数学习, 视觉－空间模板在解释几何任务中的作用强度更大。将几何任务进一步细分为轴对称与中心对称图形的任务后, 视觉－空间模板的作用就更为突显出来。这点充分说明了视觉－空间模板尽管在各种数学任务上都有作用, 但如果任务涉及到空间与几何部分, 视－空工作记忆将发挥极大的作用。随着年级升高, 视觉－空间模板的作用更能突显出来。

再次, 语音环路系统的作用表现具有领域特殊性。语音环路在综合数学以及数与代数部分作用十分明显, 并且解释力度强大, 而在空间几何任务中则并不表现明显的作用。

Andersson, U.(2010).Skill development in different components of arithmetic and basic cognitive functions:Findings from a 3-year longitudinal study of children with different types of learning difficulties.

Journal of Educational Psychology, 102

, 115‒134.Andersson, U., & Lyxell, B.(2007).Working memory deficit in children with mathematical difficulties: A general or specific deficit?

Journal of Experimental Child Psychology,96

, 197‒228.Baddeley, A.D.(1992).Working memory.

Science, 255

,556‒559.Cai, D.(2010).

A study on the cognitive processing features of junior students with mathematics learning disabilities,based on the theory of working memory

.Unpublished doctorial dissertation, East China Normal University.[蔡丹.(2010).

初中生数学学习困难的认知加工特点: 基于工作记忆的研究

.博士学位论文, 华东师范大学]Cai, D., Li, Q.W., & Deng, C.P.(2010).An exploration of individual difference theories of working memory.

Psychological Development and Education, 26

(2),205‒209.[蔡丹, 李其维, 邓赐平.(2010).工作记忆新探: 基于个体差异的研究.

心理发展与教育, 26

(2), 205‒209.]Chen, Y.H., & Wang, M.Y.(2009).The relationship between executive functions and arithmetical cognitive strategies of children.

Psychological Science, 32

(1), 34‒37.[陈英和, 王明怡.(2009).儿童执行功能与算术认知策略的关系.

心理科学, 32

(1), 34‒37.]Cornoldi, C., Dalla Vecchia R, & Tressoldi, P.E.(1995).Visuo-spatial working memory limitations in low visuo-spatial high verbal intelligence children.

Journal of Child Psychology and Psychiatry, and Allied Disciplines,36

(6), 1053‒1064.Daneman, M., & Carpenter, P.A.(1980).Individual differences in working memory and reading.

Journal of Verbal Learning and Verbal Behavior, 19

, 450‒466.De Smedt, B., Janssen, R., Bouwens, K., Verschaffel, L., Boets,B., & Ghesquière, P.(2009).Working memory and individual differences in mathematics achievement: A longitudinal study from first grade to second grade.

Journal of Experimental Child Psychology, 103

, 186‒201.Fürst, A.J., & Hitch, G.J.(2000).Separate roles for executive and phonological components of working memory in mental arithmetic.

Memory and Cognition, 28

, 774‒782.Gathercole, S.E., & Pickering, S.J.(2000).Working memory deficits in children with low achievements in the national curriculum at 7 years of age.

British Journal of Educational Psychology, 70

, 177‒194.Geary, D.C.(2004).Mathematics and learning disabilities.

Journal of Learning Disabilities, 37

, 4‒15.Geary, D.C., Hamson, C.O., & Hoard, M.K.(2000).Numerical and arithmetical cognition: A longitudinal study of process and concept deficits in children with learning disability.

Journal of Experimental Child Psychology, 77

,236‒263.Hyun, J.-S., & Luck, S.J.(2007).Visual working memory as the substrate for mental rotation.

Psychonomic Bulletin &Review, 14

(1), 154‒158.Kathleen, W.M., & Swanson, H.L.(2001).Are Mathematics Disabilities Due to a Domain-General or a Domain-Specific Working Memory Deficit?

Journal of Learning Disabilities,34

(3), 237‒248.Keeler, M.L., & Swanson, H.L.(2001).Does strategy knowledge influence working memory in children with mathematical disabilities?

Journal of Learning Disabilities,34

(5), 418‒434.Krajewski, K., & Schneider, W.(2009).Exploring the impact of phonological awareness, visual-spatial working memory,and preschool quantity-number competencies on mathematics achievement in elementary school: Findings from a 3-year longitudinal study.

Journal of Experimental Child Psychology, 103

, 516‒531.Kyttälä, M., Aunio, P., & Hautamäki, J.(2010).Working memory resources in young children with mathematical difficulties.

Scandinavian Journal of Psychology, 51

(1),1‒15.Lee, K.M., & Kang, S.Y.(2002).Arithmetic operation and working memory: Differential suppression in dual tasks.

Cognition

, 63‒68.Li, Q.(2009).

A study on the problem representation of the word-problem of the elementary school students with mathematic learning disability which is based on the PASS theory

.Unpublished doctorial dissertation, East China Normal University.[李清.(2009).

基于PASS理论的小学数学学习困难儿童应用题问题表征研究

.博士学位论文, 华东师范大学.]Liu, C.(2004).Working memory and processing speed in children with arithmetical difficulties.

Journal of Nanjing Normal University (Social Science Edition),

(3), 81‒88.[刘昌.(2004).数学学习困难儿童的认知加工机制研究.

南京师大学报(社会科学版),

(3), 81‒88.]Logan, G.D., & Cowan, W.B.(1984).On the ability to inhibit thought and action: A theory of an act of control.

Psychological Review, 91

(3), 295‒327.Mazzocco, M.M.M., & Mayers, G.F.(2003).Complexities in identifying and defining mathematics learning disability in the primary school-age years.

Annals of Dyslexia, 53

,218‒253.McLean, J.F., & Hitch, G.J.(1999).Working memory impairments in children with specific arithmetic learning difficulties.

Journal of Experimental Child Psychology, 74

,240‒260.Meyer, M.L., Salimpoor, V.N., Wu, S.S., Geary, D.C., &Menon, V.(2010).Differential contribution of specific working memory components to mathematics achievement in 2nd and 3rd graders.

Learning and Individual Differences, 20

(2), 101‒109.Monette, S., Bigras, M., & Guay, M.C.(2011).The role of the executive functions in school achievement at the end of Grade 1.

Journal of Experimental Child Psychology, 109

,158‒173.Owen, A.M., McMillan, K.M., Laird, A.R., & Bullmore, E.(2005).N-back working memory paradigm: A meta-analysis of normative functional neuroimaging studies.

Human Brain Mapping, 25

, 46‒59.Passolunghi, M.C., & Siegel, L.S.(2001).Short-term memory, working memory and inhibitory control in children with difficulties in arithmetic problem solving.

Journal of Experimental Child Psychology, 80

, 44‒57.Passolunghi, M.C., & Siegel, L.S.(2004).Working memory and access to numerical information in children with disability in mathematics.

Journal of Experimental Child Psychology, 88

, 348‒367.Passolunghi, M.C., Vercelloni, B., & Schadee, H.(2007).The precursors of mathematics learning: Working memory,phonological ability and numerical competence.

Cognitive Development, 22

, 165‒184.Raghubar, K.P., Barnes, M.A., & Hecht, S.A.(2010).Working memory and mathematics: A review of developmental, individual difference, and cognitive approaches.

Learning and Individual Differences, 20

,110‒122.Reuhkala, M.(2001).Mathematical skills in ninth-graders:Relationship with visuo-spatial abilities and working memory.

Educational Psycholog

, 21

, 387‒399.Simmons, F.R.Willis, C., & Adams, A.M.(2012).Different components of working memory have different relationships with different mathematical skills.

Journal of Experimental Child Psychology, 111

, 139‒155.Song, G.W., He W.G., & Kong, W.(2011).Influence of problem representation and working memory span on pupils’ mathematical problem solving.

Acta Psychologica Sinica, 43

(11), 1283‒1292.[宋广文, 何文广, 孔伟.(2011).问题表征、工作记忆对小学生数学问题解决的影响.

心理学报, 43

(11), 1283−1292.]St Clair-Thompson, H.L.(2011).Executive functions and working memory behaviours in children with a poor working memory.

Learning and Individual Differences, 21

, 409‒414.Swanson, H.L., & Beebe-Frankenberger, M.(2004).The relationship between working memory and mathematical problem solving in children at risk and not at risk for serious math difficulties.

Journal of Education Psychology,96

(3), 471−491.Swanson, H.L., & Sachse-Lee, C.(2001).Mathematical problem solving and working memory in children with learning disabilities: Both executive and phonological processes are important.

Journal of Experimental Child Psychology

, 294−321.Wang, E.G., & Liu, C.(2011).On working memory in children with mathematics disabilities.

Advances in Psychological Science, 13

(1), 39‒47.[王恩国, 刘昌.(2005).数学学习困难与工作记忆关系研究的现状与前瞻.

心理科学进展, 13

(1), 39‒47.]Wang, E.G., Zhao, G.X., Liu, C., Lv, Y., & Shen, D.L.(2008).Different types of learning difficult youth have different deficits of working memory.

Chinese Science Bulletin,53

(14), 1673‒1679.[王恩国, 赵国祥, 刘昌, 吕勇, 沈德立.(2008).不同类型学习困难青少年存在不同类型的工作记忆缺陷.

科学通报,53

(14), 1673‒1679.]Wilson, K.M., & Swanson, H.L.(2001).Are mathematics disabilities due to a domain-general or a domain-specific working memory deficit?

Journal of Learning Disabilities,34

(3), 237‒248.Xu, S.(2006).

The study on pupils’ mathematics learning

.Hangzhou: Zhejiang University Press.[徐速.(2006).

小学数学学习心理研究

.杭州: 浙江大学出版社.]Yu, G.L., & Zeng, P.P.(2003).Visual-spatial representations and mathematical problem solving among mathematical learning disabilities.

Acta Psychologica Sinica, 35

(5),643‒648.[俞国良, 曾盼盼.(2003).数学学习不良儿童视觉-空间表征与数学问题解决.

心理学报, 35

(5), 643‒648.]Zhang, M., & Sui, J.(2003).Differences of the visuospatial working memory among students with learning disabilities and excellent students on the divided attention conditions.

Chinese Journal of Applied Psychology, 9

(1), 29‒34.[张明, 隋洁.(2003).分散注意条件下学优生与学困生视空间工作记忆的比较研究.

应用心理学, 9

(1), 29‒34.]Zhao, Y., & Cai, X.Y.(2010).The effect of disciplinary domain knowledge and mathematical achievement on working memory span.

Psychological Development and Education, 26

(1), 70‒76.[赵燕, 蔡笑岳.(2010).学科领域知识和学业成绩对工作记忆广度的影响.

心理发展与教育, 26

(1), 70‒76.]Zheng, X.H., Swanson, H.L., & Marcoulides, G.A.(2011).Working memory components as predictors of children’s mathematical word problem solving.

Journal of Experimental Child Psychology, 110

, 481‒498.Zuo, Z.H.(2006).

A study on the cognitive processing mechanism of pupils with mathematics learning disabilities

.Unpublished doctorial dissertation, East China Normal University.[左志宏.(2006).

小学生数学学习困难的认知加工机制

.博士学位论文, 华东师范大学.]