梁振动问题的MOL数值方法

李麦侠, 曲小钢

(西安建筑科技大学 理学院， 陕西 西安 710055)

0 引言

本文采用直线法(Method of Lines,简称MOL)对空间域进行离散，并利用四阶龙格-库塔方法可以长时间精确计算的特点，实现了对梁振动问题高精度、稳定地求解.

1 MOL数值解法

设在矩形区域G{0≤x≤1;0≤t≤T}内研究如下梁振动方程的初边值问题.

其中,φ1(x)、φ2(x)、g1(t)、g2(t)、g3(t)、g4(t)

是给定函数[4]，φ1(x)、φ2(x)为初值,g1(t)、g2(t)、g3(t)、g4(t)为边界值.

采用直线法对空间导数进行离散[5,6].

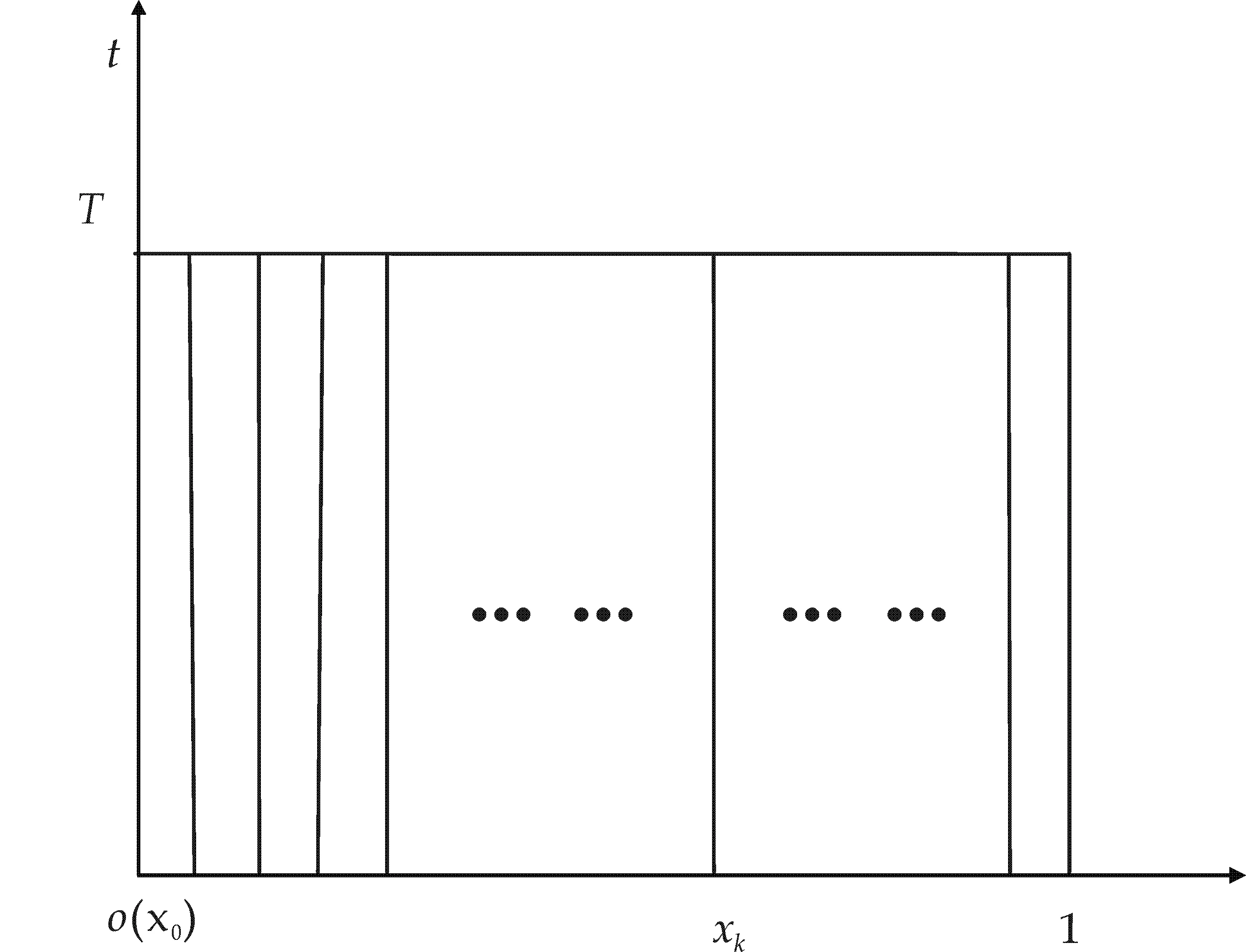
图1 空间变量x的剖分图

假定问题(Ⅰ)有充分光滑解u(x,t),可按直线法思路来求解.在方程(Ⅰ)中令x=xk,并利用如下二阶中心差商：

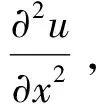
2u(xk+1,t)+4u(xk,t)-2u(xk-1,t)+u(xk,t)-2u(xk-1,t)+u(xk-2,t)]=

4u(xk-1,t)+u(xk-2,t)]

再令uk(t)=u(xk,t),可得方程：

o(Δx4) (k=2,…,N-2)

(5)

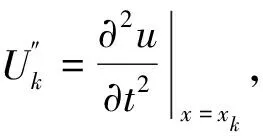
(6)

利用初始条件(2)可得：

(7)

利用边界条件(3)可得：

U0(t)=U(0,t)=g1(t)UN(t)=U(1,t)=g2(t)

(8)

利用边界条件(4)及一阶向前差商可得：

g3(t)

(9)

g4(t)

(10)

具有边界条件 (8)、(9)、(10)的方程组(6)是以o(Δx4)的精确度逼近问题(Ⅰ),此方程组称为直线法方程组.(7)、(8)、(9)、(10)式共同构成了常微分方程组的初边值问题,要得到此方程组的解析解u(xk,t)(k=1,2,…,N-1)相当困难.

由于常微分方程初边值问题数值解的算法已相当成熟,其中龙格-库塔法[7]被证明是具有精度高、收敛、稳定(在一定条件下)、计算过程中可以改变步长、不需要计算高阶导数等优点的一种方法,故本文采用四阶龙格-库塔法求解以上的常微分方程边值问题的近似解u(xk,tj).

下面考虑更一般的一阶常微分方程组的初边值问题：

其四阶龙格-库塔法数值求解公式[8]为：

yi,m+1=yim+(h/6)(ki1+2ki2+2ki3+ki4)

其中

(i=1,2,…,n;m=0,1,2,…)

其中，yim是第i个函数yi在节点tm=t0+mh处的近似值,h为积分步长.

根据上面的计算过程及公式，就可以进行计算机编程，其具体步骤如下：

(1)对直线x=xk时的方程，用二阶中心差商代替x的偏导数，得到线性常微分方程组；

(2)Matlab编程,用龙格-库塔方法求解常微分方程组，得到数值解；

(3)调出数值解且与真值比较[9]，得到误差分析.

按以上的步骤，便可求出线性梁振动方程的数值解.

2 上机实现

利用Matlab语言编写了上述线性二阶常微分方程组边值问题数值解的程序,从而可得到u在t所属区间[0≤t≤T]上的节点{t0=0,t1=Δt,…,tj=jΔt,…,tM=MΔt}上的近似解u(xk,tj)，其中Δt=T/M.

3 收敛性及误差分析

设rk(t)=u(xk,t)-Uk(t)，由Taylor展开式[10,11]得到rk(t)的方程组

(11)

(12)

r2(t)-r1(t)+r0(t)=0,

rN(t)-2rN-1(t)+rN-2(t)=0

(13)

其中,k=0,1,2,…,N;此时0≤x≤1,0≤t≤T.

假定下式[12,13]

(14)

由(11)、(12)、(13)和Cauchy不等式[6]、微分(14) ，得到：

因为I(0)=0，所以

(15)

其次，根据r0(t)=rN(t)=0，得到：

因此，由Cauchy不等式

最终得到如下估计：

4 结束语

本文给出了求梁振动问题的一种新的方法，即直线法.它具有精度高,编程简单,易于计算机实现等特点,特别适用于非线性方程的数值求解,是一种实用有效的数值求解方法.

[1] 倪 平，高仪新.解梁的振动方程的广义方法(I)[J].东北师范大学学报(自然科学版)，1995(4):14-19.

[2] 曾文平.四阶杆振动方程的含参数四层显式差分格式[J].华侨大学学报(自然科学版)，2002,23(2):116-121.

[3] 曾文平.解四阶杆振动方程新的两类隐式差分格式[J].华侨大学学报(自然科学版)，2003,24(2):136-142.

[4] 邹 佩，曲小钢.梁振动问题的拟小波-精细时程积分法[J].陕西科技大学学报(自然科学版)，2011,29(6):140-144.

[5] 彭亚绵，闵 涛，张世梅，等.Burgers方程的MOL数值解法[J].西安理工大学学报，2004,20(3):276-280.

[6] 南京大学数学系.偏微分方程数值解法[M].北京:科学出版社，1979：393-417.

[7] 易晋生，顾安邦，王小松.基于MATLAB的公路桥梁车桥耦合数值计算方法[J].重庆交通大学学报(自然科学版)，2012,31(6):1 101-1 104.

[8] 毋玉芝.四阶龙格-库塔算法的C语言实现[J].焦作大学学报,2001,15(1):55-57.

[9] 单双荣.梁振动方程的多辛Fourier拟谱算法[J].华侨大学学报(自然科学报)，2006,27(3):234-237.

[10] 许士菊，王长华.梁振动方程的一个稳定的有限差分近似[J].吉林化工学院学报，2007,24(1):79-81.

[11] 周良强，陈予怒，陈芳启.梁振动方程的多参数高精度格式[J].安庆师范学院学报(自然科学版)，2010,16(2):62-65.

[12] 戴嘉尊，邱建贤.微分方程数值解法[M].南京:东南大学出版社，2002.

[13] 孙志忠.偏微分方程数值解法[M].北京:科学出版社，2005.