自成像结构光投影及相移的实现方法

吕 岑， 纪明明， 何 晶

(陕西科技大学 电气与信息工程学院， 陕西 西安 710021)

0 引言

光栅投影法是测量三维轮廓的一种非接触式测量方法，它具有分辨率高、非接触性和数据获取速度快等优点，广泛应用于机器视觉、工业过程控制、人体测量医疗诊断和现代制造等方面[1].随着光学技术和计算机技术的兴起与发展，以光栅投影法为代表的光学三维非接触式测量技术得到了广泛发展.

光栅相移法是在20世纪80年代发展起来的，M.Takeda等[2]于1983年提出傅立叶轮廓测量法，V.Srinivasan等[3,4]于1984～1985年提出光栅相移法轮廓测量法.两者都是使用正弦条纹光栅进行投射，利用投射光场中物体表面对光栅调制后相位发生变化来解算物体表面的三维信息.相移法是解算正弦光栅相位信息的有效方法，具有良好的抗噪性，是当今发展最快的光学三维测量方法之一.

本文首先介绍了光栅相移法的原理，其次对相移的实现原理和实现方法做了分析，最后通过实验验证相移方法的可行性.

1 光栅相移法的原理

光栅相移法[5,6]是利用投影多幅光栅图像(每两幅光栅之间有确定的相位差)来解调相位，获得包裹的相位主值.假设投影的光栅为正弦光栅，分N次进行投影，则相邻两幅光栅的相位差为2π/N，令Ii代表第i(i=1,…,N)幅图像上某点的光强.

Ii(x,y)=A(x,y)+B(x,y)cos(φ(x,y)+2πi/N)

(1)

式(1)中：A(x,y)是背景光强；B(x,y)是条纹图的振幅；φ(x,y)是受被测物体表面高度调制的光条纹的相位.相位φ(x,y)对应物体上各点的高度h(x,y)，通过对φ(x,y)的处理就可获得物体的三维信息.

已知光条纹的光强分布时，还有三个参数是未知的，这样为了得到相位，至少需要有三个相互独立的信息提供，当N≥3时，根据式(1)组成的方程组，可以求解得到相位的计算公式：

(2)

为了从相位函数计算被测物体的高度分布，必须将由反三角运算引起的包裹相位恢复成真实相位分布，这一过程称为相位展开(Phase Unwrapping)，即解相位.解相位后，可获得变形光栅条纹中各点的真实相位.由此，可获取被测物体的真实高度信息.

本文以N=4的四步相移法[7,8]为例，即将光栅沿垂直参考面条纹方向在一个周期内移动四次，每次移动四分之一周期的距离，这样可以得到四个相移光栅场，采集到四幅相移图，分别表示为：

I1(x,y)=A(x,y)+B(x,y)cosφ(x,y)

(3)

I2(x,y)=A(x,y)+B(x,y)cos(φ(x,y)+π/2)

(4)

I3(x,y)=A(x,y)+B(x,y)cos(φ(x,y)+π)

(5)

I4(x,y)=A(x,y)+B(x,y)cos(φ(x,y)+3π/2)

(6)

由上述四式，得到相位函数的表达式为：

(7)

在采用干涉型结构光场方法或光栅投影结构光场方法中，这种相移是通过改变参考光波的光程四分之一波长，或横向移动光栅四分之一光栅常数的距离实现的.这就要求采用高精度(其精度至少为0.01微米)的相移器来完成.如果达不到精度要求，将会带来因无法抑制条纹飘移和抖动对测量误差的影响这一致命弱点.

2 投影与相移的实现

根据倾斜平行光照射下光栅自成像原理，本文采用平移照明光源狭缝的方法改变条纹位置，实现相移，并使用短焦距物镜将光栅自成像投影，解决了现有的结构光投影系统的体积大、成本高、相移精度要求高等技术问题.

2.1 实现原理

1836年，泰伯(Talbot)发现用一束单色平面波垂直照明周期为d的光栅时，在光栅后ZT=2md2/λ(m为整数)距离的平面上会出现清晰的光栅像.这一现象就是光栅自成像现象，或称为泰伯效应[9-11].泰伯效应广泛应用于激光校准性校验、长度测量，以及和莫尔条纹相结合实现对透镜焦距、曲率半径、波像差的测量等[12].

假设单色平面光波以倾斜θ角度入射到光栅G1上，则入射光的波场可表示为[11-14]:

exp[(2πi/λ)θ·x]

(8)

紧贴光栅G1后表面的光波场为：

(9)

因此，光栅后任意位置处的菲涅耳衍射场为：

(10)

积分限为±∞的菲涅耳积分产生的无关紧要的常数因子，可以忽略，则剩下的部分为：

(11)

如果距离z为泰伯距离，式(11)可重写为：

(12)

式中：B=exp[(iπ/λ)(2θ·ξ-θ2·zT)]

当平行光倾斜于光轴小角度θ入射时，自成像在垂直于光轴的横向上会产生位移，即条纹发生横向平行移动，其横向位移量为Δx≈ZTθ≈2md2θ/λ，可见条纹的位移，即相移与平行光倾斜角成正比.

如图1所示，狭缝G0置于焦距为f的柱面透镜焦平面上，则中心处狭缝光源经透镜后形成平行于光轴的平光，垂直照射光栅G1，在泰伯距离处得到光栅像G1′；位于距光轴ξ位置处的某个狭缝光源经透镜后形成倾斜角为θ≈tanθ=ξ/f的平面光波，倾斜照射光栅G1时在泰伯距离处得到光栅像G1″，其相对于G1′的位移量Δx为：

Δx=ZTθ=ZTξ/f=2md2ξ/λf=ξ/M

(13)

式中,M=λf/2md2=f/ZT，我们称之为位移(相移)放大率.实际使用时，由于自成像距离一般是几个毫米甚至更小，而透镜焦距是几十甚至几百毫米，故相移(位移)放大率可达几十至几百倍，对精度的要求随之降低几十至几百倍，用一般普通的位移平台即可满足要求.

具体实现过程如下：

(1)平移单狭缝使条纹平移一个条纹间距(2π相移)，此时平行光和光轴夹角为θ.

(2)记录狭缝平移距离H数值(多做几组,求平均值)，可求出θ数值.

(3)狭缝平移D=H/4=fθ/4时,可以实现相移π/2.

(4)同理,可以将单缝扩展成缝等间距为H的整数倍的多缝，提高光栅自成像的亮度，利于提高测量精度.

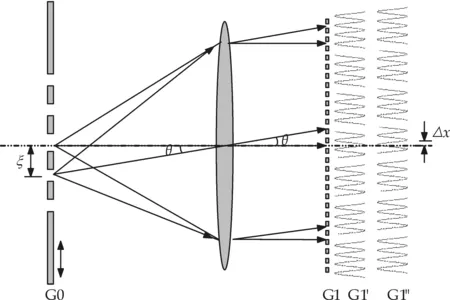
图1 相移的实现原理图

2.2 实现方法

本文所用的实现相移的系统如图2所示.该系统主要包括光源、狭缝、柱面透镜、投影光栅、显微物镜和接收屏.其中光源可以为红色LED光源或激光光源；投影光栅选择光栅常数为30μm的正弦光栅；显微物镜主要用于将投影光栅在物镜焦平面上的自成像投影至待测物体之上，在实验过程中使用放大倍数为40的显微物镜；接收屏用来接收所获得的光栅图.

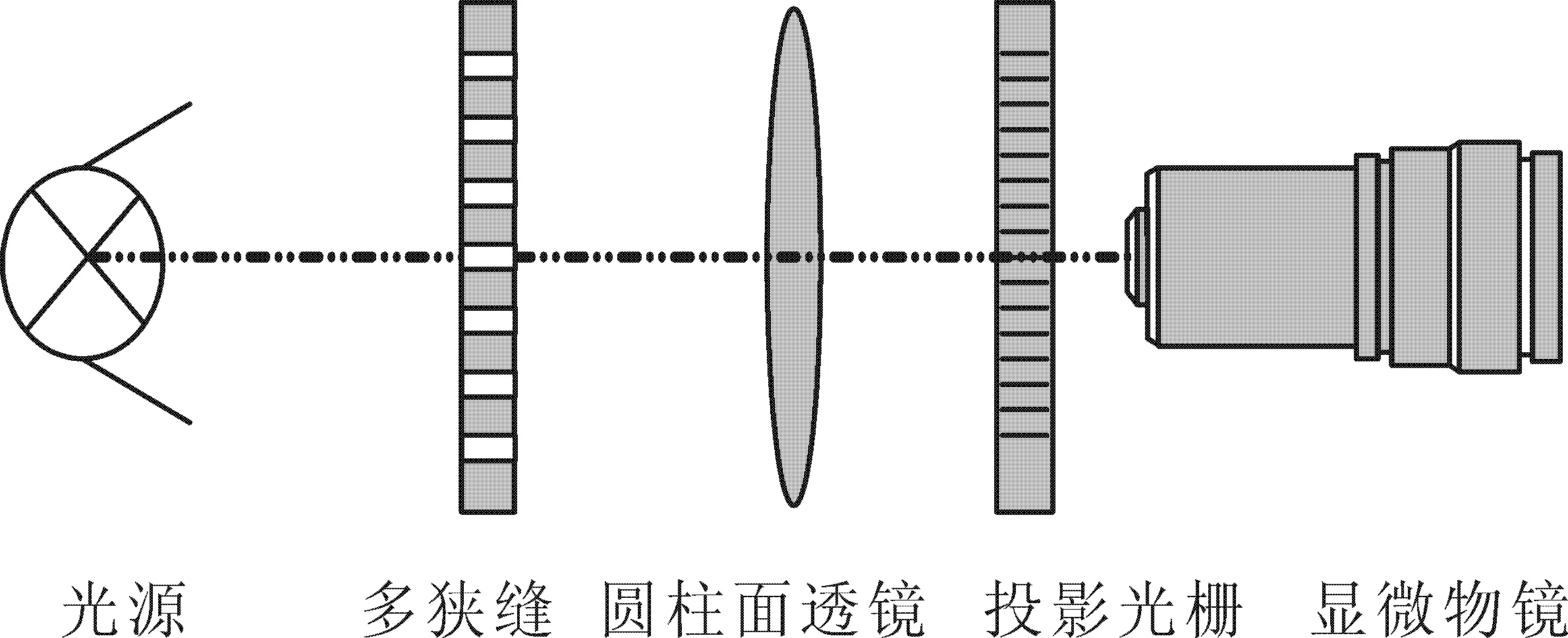
图2 相移的系统结构图

通过实验测量，可计算得D=0.86 mm.也就是说，狭缝移动D，可恰好使得相位平移π/2.同理，可以设计等间距宽的多缝，缝间距是4D.多缝既可以增加条纹的亮度，又可以在平移时实现平移π/2相移.

缝宽的确定原则是满足小于D/2大于0，以满足光的空间相干性.本实验中，可根据实验光路以及条纹对比度确定一个合适的缝宽.在实验过程中，不断改变狭缝的宽度，观察到：当缝宽设计小于0.43 mm时条纹可见度逐渐变大，并经过不断改进，得出在缝宽为0.20 mm时条纹可见度明显增大，说明这个值接近允许宽度.在实验中，选择狭缝的宽度为0.20 mm.

由实验可得光栅投影平移一个条纹狭缝计算值为4D=3.44 mm.平移3.44 mm后，光栅投影的变化如图3所示.

图3 实验验证狭缝平移3.44 mm后光栅投影平移距离变化

从实验观察到，在移动狭缝3.44 mm后，光栅投影平移近似一个条纹.从而可验证3.44 mm与理论值基本相符.同理,通过移动D=0.86 mm,就能满足四步相移.在实际使用过程中，采用多狭缝、光栅、柱面透镜和显微物镜这些体积较小的常用光学元件，使得结构简单、成本低，能缩小整个投影装置的体积，易于实现装置集成化.

3 结论

光栅相移法是光学三维测量中的一项重要技术.本文从光栅投影法的原理出发，给出了一种不需要精密相移装置的相移方法.

通过设置狭缝的宽度和狭缝移动的距离实现相位的移动.由实验结果可以知道，当狭缝的宽度设置为0.20 mm，狭缝移动3.44 mm时，光栅投影移动近一个条纹；当狭缝移动0.86 mm时，可以实现四步相移.这样就不需要使用精密的相移装置，就可以实现相移，解决了现有结构光投影系统的设备复杂的技术问题.

[1] 田爱玲,刘 洋,郭迎福,等,双CCD光栅投影法测量物体三维轮廓技术[J].西安工业大学学报,2009,29(2):108-112.

[2] Takeda M,Mutoh K.Fourier transform profilometry for automatic measurement of 3D object shapes[J].Applied Optics,1983,22(24)：3 977-3 982.

[3] Srinivasan V,Liu H C,Halioua M.Automated phase measuring profilometry of 3D diffuse object[J].Applied Optics,1984,23(18)：3 105-3 108.

[4] Srinivasan V,Liu H C,Halioua M.Automated phase measuring profilometry:a phase mapping approach[J].Applied Optics,1985,24(2)：185-188.

[5] 陈益松,夏 明,林 琳.光栅相移法用于三维人体测量的实验研究[J].纺织学报,2013,34(6):83-87.

[6] 吴双卿.光栅投影三维形貌测量技术的研究[D].四川：西南交通大学，2003.

[7] 蔡长青,贺玲凤.基于四步相移法的相位差值提取方法[J].华南理工大学学报(自然科学版),2011,39(9):93-96.

[8] 盖绍彦,达飞鹏.一种新的相位法三维轮廓测量系统模型及其标定方法研究[J].自动化学报，2007,33(9):68-73.

[9] 方靖岳.光栅大小对琅奇光栅泰伯效应的影响分析[J].红外与激光工程，2010,39(5):23-26.

[10] 陈 然.Talbot效应研究与新进展[J].激光与电子学进展,1996,12(8):17-22.

[11] Yoshiaki Nakano,Kazumi Murata.Measurements of phase objects using the Talbot effect and moire techniques[J].Applied Optics,1984,15(2):2 297-2 299.

[12] 冯 婕,周仁魁,赵建科,等.对Talbot自成像和几何成像关系的分析[J].光子学报.2008,37(11):2 332-2 335.

[13] 罗先刚,陈旭南,姚汉民.部分相干光倾斜照明成像研究[J].微细加工技术，1997,14(4):55-62.

[14] 陈万金,闵春宗.非理想照明条件下的Talbot距离的确定[J].松辽学刊(自然科学版)，1997,10(1):65-69.