轴向运动纸幅－气垫耦合系统平衡态分析∗

李路雷，蔡忠清，惠 升，徐培民

（安徽工业大学机械工程学院，安徽马鞍山 243002）

轴向运动纸幅－气垫耦合系统平衡态分析∗

李路雷，蔡忠清，惠 升，徐培民

（安徽工业大学机械工程学院，安徽马鞍山 243002）

造纸工业中采用正弦气浮干燥器对纸幅进行非接触传输并干燥时，轴向运动纸幅的横向变形与干燥器气垫区域的气体压力是相耦合的。为获得平衡状态下的纸幅变形和气垫区压力分布这两项重要的工艺参数，需要将纸幅和气垫作为一个相互耦合的系统来研究。考虑一维模型，将纸幅近似为恒张力作用下的轴向运动Euler－Bernoulli梁，并设气垫区域的气体压力满足不可压缩非定常流动的连续性方程和N－S方程，建立了纸幅和气垫的控制方程及耦合条件。采用有限差分法和Newton－Raphson法对气垫区的平衡压力和纸幅变形进行数值求解。最后，对纸幅传输速度，纸幅牵引张力等运行参数对所述系统平衡态的影响进行了讨论。

纸幅变形；气垫压力；耦合系统；平衡态

1 引 言

气垫干燥器广泛应用于热处理线上非接触稳定地支承、传输并干燥塑料、纸张等带状制品，以保证带状制品表面涂层质量［1］。作为气垫干燥器的一种，正弦曲线气浮干燥器广泛应用于涂布纸，特别是铜板纸干燥过程［2］。由于纸幅抗弯刚度小且跨度大，在气垫区压力的作用下，不可避免地会发生弯曲变形，甚至产生振动，纸幅的弯曲变形和振动会进一步导致气垫区压力分布不均。因此，纸幅的变形和气垫区压力分布的变化是相互耦合的。传统的针对刚性壁面计算气垫压力分布的附壁边界理论［3］不再适用。为保证纸幅在干燥过程中表面不受擦伤并保持高速稳定运行，必须在考虑纸幅变形的基础上来计算气垫区的压力分布。理论上，这需利用气垫区夹带空气处的连续性条件和平衡条件的微分形式来建模，并联立求解纸幅的控制方程和气垫区的压力方程［4］，即对纸幅－气垫耦合系统进行平衡态分析。这也是进一步对该耦合系统进行动力学分析的基础。

HYUN－Ki CHO［5］以轴向运动的带状制品越过一个压力气垫箱为研究对象，通过弹性理论和流体动力学建立了系统的气弹性力学模型，通过有限差分法对系统平衡态进行求解。然而，由于其研究对象略显简单，并没有考虑相邻气垫区间的压力耦合，因此并不能完全适用于工程中较为常用的正弦曲线气浮干燥器。

磁带驱动器中磁带和其跨度间的单个记录头所组成的耦合系统与纸幅－气垫耦合系统类似，其平衡态的研究主要集中在为确定磁带平衡变形和平衡压力分布的计算方法上。Stahl［6］采用基于磁带和雷诺方程空间离散的有限差分法对流体非定常控制方程进行离散，得到空间节点的一系列常微分方程，并对时间积分，直至达到稳定状态。此种方法虽可经受数值不稳定的考验，但却需要大量计算。Adams［7］则采用有限单元法对磁带和雷诺方程稳态形式离散得到系统的耦合、非线性的代数方程，并采用Newton－Raphson方法进行求解，由于雅可比矩阵是显式的，因此此种方法求解速度得到了提高。Lakshmikuma⁃ran［8］采用节点自动分配的方法来减少非线性方程的数目，从而提高了求解磁带平衡态位形和气体平衡压力的速度，发展了求解系统平衡态并可减小计算工作量的数值求解方法。

本文以正弦气浮干燥器对纸幅进行气浮非接触干燥为背景，以纸幅与两个相对交错布置的气垫箱所组成的耦合系统为研究对象，建立其数学模型，并对系统的平衡态进行分析求解，得到气垫区的压力分布和纸幅的变形，为工程中同类或更为复杂的气垫干燥系统的分析和设计提供理论依据。

2 纸幅－气垫耦合系统建模

在采用气浮干燥器对纸幅进行气浮干燥的生产线上，由于两传送辊之间的纸幅长宽比较大，为便于问题的分析及模型的简化，考虑一维模型，将纸幅视为恒定张力牵引下并以恒定速度轴向移动的Euler－Bernoulli梁，纸幅两端边界可视为铰支，并考虑正弦气浮干燥器的典型布置，建立如图1所示的最简单力学模型。

图1 轴向运动纸幅－气垫耦合系统力学模型示意图

纸幅在恒定牵引张力F的作用下以恒定的速度vp越过由两个相对交错布置的气垫箱所组成的气垫箱组，两气垫箱工作表面与纸幅的初始距离均为δ，气垫箱喷口间距为wa。纸幅在其跨度空间x∈（0，L）上的变形用y（x，t）表示；气体在气垫区域x∈（xLi，xRi）上所形成的气垫压力用pi（x，t）表示，气垫箱工作表面与纸幅间距用hi（x，t）表示。

2.1 纸幅的控制方程

设纸幅截面面密度为m，单位宽度上的抗弯刚度为EI，张力为T，跨度上的压力分布为pp（x，t），则轴向匀速运动纸幅横向振动的控制方程［9］为：

由于pp（x，t）仅在x∈（xL1，xR1）∪（xL2，xR2）上存在，因此，根据单位阶跃函数H（x）的加窗特性［10］，pp（x，t）可表示为：

据此，方程式（1）可进一步表示为：

由于纸幅两端视为铰支，则有边界条件

2.2 气垫区域气体的控制方程

正弦曲线气浮干燥器在工作过程中气垫区气体的流动形态较为复杂。为便于问题分析，引入如下假设：①气体是不可压缩的粘性牛顿流体，且满足流体的连续性方程和N－S方程；②气垫箱足够宽，即气体的侧流可以忽略不计；③气流几乎全部平行于x轴流动，并忽略气流的横向压力梯度，认为气体压力仅是截面位置x的函数；④气浮干燥器在工作过程中，通过压力控制系统的调节控制，气垫箱供应压力保持恒定。

根据以上所作假设，并由流体的连续性方程和N－S方程，在气垫区域x∈［xLi，xRi］上的气体控制方程［5］为：

Qi为流经气垫箱单个喷口的流量：

其中：ρ为空气密度；ν为空气的运动粘度；b为喷口宽度；Cd为喷口的流速系数。

摩擦系数fi取决于流体的流动状态，需以流量Qi的形式来表达，工程中气垫区气体的流动以湍流为主，故摩擦系数fi可表示为［5］：

由图1可知，纸幅的横向变形和气垫层厚度之间有如下耦合条件：

2.3 纸幅和气体控制方程无量纲化

为便于问题的分析以及书写的简洁，以无量纲的形式来表示纸幅和气体的控制方程式（3）～（9），引入独立变量：

通过上述变量及参数的定义，纸幅－气垫耦合系统控制方程可以以无量纲的简洁形式来表示，其中，在∈（0，1）上，轴向移动纸幅的无量纲的动力学方程：

3 平衡态分析

将式（20）、（23）和（25）代入方程式（26）中，气体在气垫区的平衡压力可表示为：

方程式（27）是一阶微分方程，对其求解则需要一个边界条件，这个条件可由附壁边界理论给出，应用Stanton－Jones的厚壁喷口理论［3］，有：

以上就是纸幅－气垫耦合系统的气弹性方程，格林函数法是求解此类带有边界条件非齐次微分方程的有效方法。为构建方程式（22）的格林函数，可将其表示成如下形式

式中：α＝，与纸幅的材料、结构及运行参数有关。

与方程式（29）相关联的格林函数为：

方程式（30）表示在≤有单位集中载荷。

由于方程式（30）是线性非齐次微分方程，故满足叠加原理。将方程式（30）写成一般形式：

根据单位阶跃函数的性质，以及两端简支轴向移动Euler－Bernoulli梁的边界条件（17）、在处的连续性条件及剪力条件，可得方程式（31）的解，即两端简支轴向移动Euler－Bernoulli梁的格林函数［4］为：

格林函数又可称为结构影响系数或柔度，它表示纸幅在处作用一单位集中力时，纸幅在 处的弯曲变形。

由式（29），纸幅的实际变形可以以气垫压力卷积的形式来显示表达：

这样，由于纸幅的实际变形可以以气垫压力卷积的形式来显示表达，通过上述方式，将纸幅的变形嵌入到压力方程中，从而避免弹性方程和压力方程间的迭代联立求解。此外，由于采用这样的方法只有压力被离散化，因此，数值求解系统的平衡态只需要较少的自由度。

4 有限差分法数值求解

4.1 有限差分法离散

为便于对压力方程式（34）进行数值求解，将纸幅在其跨度空间离散化，纸幅跨度区间及其区间节点数如表1所示。表中：总节点数N＝n1＋n2＋n3＋n4＋n5。

表1 节点在纸幅跨度上的分布

与空间节点n所对应的无量纲坐标为：

平衡压力式（34）和式（35）可用前差分方法和梯形公式离散，对于n＝n1＋1，n1＋2，…，n1＋n2－1：

由式（40）、（41）、（45）、（46）中可以看出，不仅气垫区1和气垫区2的气体压力与纸幅相耦合，而且，气垫区1和气垫区2的气体压力通过纸幅的变形同样是相互耦合的。

4.2 Newton－Raphson法数值求解

平衡态的数值求解可采用Newton－Raphson数值方法［11］来计算

是一系列非线性代数方程。计算时从所估计的初始压力开始迭代计算，直至平衡压力偏差在误差所设定的允许范围之内。

4.3 计算实例及讨论

对纸幅－气垫耦合系统的平衡态采用有限差分法和Newton－Raphson法进行数值仿真分析，图1所示纸幅－气垫耦合系统相关参数如下［5］：L＝0.380 m，m＝0.15 kg／m2，EI＝8.64×10－4N·m，T＝30 N／m，vp＝0，xC1＝0.25L，xC2＝0.75L，p01＝690 Pa，p02＝690 Pa，wa＝0.1m，b＝0.003 m，Cd＝0.85，σ＝0.002 m，ρ＝1.21 kg／m3，v＝1.514×10－5m2／s。根据以上参数，数值求解所得到平衡态时气垫区域的压力分布和纸幅在其跨度上的变形如图2、图3所示。

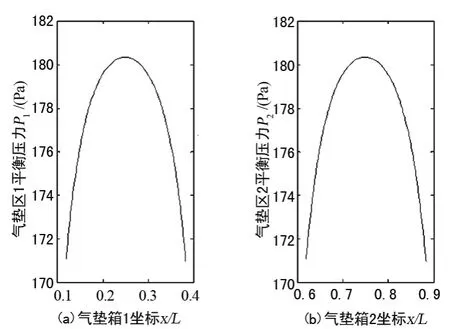
图2 气垫区压力分布

图3 纸幅在其跨度上的变形

由于气垫箱1和气垫箱2的中心位置分别位于纸幅跨度的1／4，3／4处，且平衡态时纸幅的速度为0，因此，图2所示的气垫区1和气垫区2的压力分布均呈现中间高、两端低的趋势，并且关于各自气垫中心对称。由于作用在纸幅跨度上的气垫压力载荷呈反对称分布，因此，图3所示的纸幅弯曲变形呈现为一个完整的正弦波状曲线。

纸幅在运行过程中，其运行速度和牵引张力是两项极为重要的操作参数。下面针对这两项参数对系统平衡态的影响进行分析。由于工程中的气垫箱均呈现对称布置，气垫区1和气垫区2的压力分布基本一致，因此，下文仅给出气垫区1的压力分布。

4.3.1 纸幅速度对系统平衡态的影响

仅改变纸幅传输速度，其他参数保持不变，所得纸幅速度对系统平衡态的影响如图4、图5所示。

图4 纸幅速度对气垫区压力的影响

从图4中可以看出，随着纸幅移动速度的增加，气垫区的压力逐渐减小，并且压力减小的速度急剧增加。从图5中可以看出，随着纸幅移动速度的增加，纸幅的变形逐渐增大。究其原因，从方程式（1）中可以看出，如果运动速度足够大而达到纸幅的临界速度vc，纸幅可能发生压杆失稳现象，因此，随着纸幅速度的增加，纸幅的稳定性变差，相应的变形越来越大。纸幅变形的增大，又会使气垫区高度逐渐增加，从而导致气垫区压力的减小。因此，为便于生产现场纸幅的稳定和气垫区压力的维持，实际操作中，纸幅的移动速度不宜太高。

图5 纸幅速度对纸幅变形的影响

4.3.2 纸幅牵引张力对系统平衡态的影响

改变纸幅牵引张力，其他参数保持不变，所得纸幅牵引张力对系统平衡态的影响如图6、图7所示。

图6 纸幅牵引张力对气垫区压力的影响

图7 纸幅牵引张力对纸幅变形的影响

从图6、图7中可以看出，随着牵引张力的增加，纸幅的变形逐渐减小，而气垫区的压力则逐渐增加。这是因为，纸幅张力的增加提高了系统的刚度，纸幅的变形相应减小，纸幅变形的减小使得纸幅和气垫箱工作表面的间距减小，从而使得气垫区的压力得以提高。因此，生产现场在工艺参数调整时，在保证纸幅强度的条件下适当增加纸幅张力有利于维持气垫区的压力稳定。

5 结 论

以工程中应用较为广泛的正弦气浮干燥器对纸幅进行气浮非接触干燥为背景，对纸幅－气垫耦合系统进行建模，建立了纸幅和气垫区气体的控制方程和边界条件，采用有限差分法对压力方程进行空间离散，并采用Newton－Raphson法对系统平衡态进行数值求解，获得了气垫区的压力分布和纸幅的平衡位形。最后针对纸幅移动速度和纸幅张力对气垫区压力分布和纸幅变形的影响进行了讨论，结果发现减小纸幅牵引速度并提高的纸幅的牵引张力有利于气垫区压力的维持和纸幅稳定性的提高。

［1］ 孙 强，李 俊，刘华飞，等.热镀锌带钢气垫稳定装置气体动力性能研究［J］.工业炉，2011，33（5）：5－9.

［2］ 孙卫国.SCAF干燥器在涂布纸干燥中的应用［J］.中华纸业，2002，23（8）：45－46.

［3］ Chang Y B，Moretti P M.Aerodynamic Characteristics of Pressurepad Air Bars［J］.ASME Journal of Applied Mech－anics，2000，67（1）：177－182.

［4］ Wickert J A.Free Linear Vibration of Self－Pressurized Foil Bearings［J］.ASME Journal of Vibration and Acoustics，1993（115）：145－151.

［5］ Hyun K C.Flow－Include Vibration of a Web Floating Over a Pres⁃sure－Pad Air Bar［D］.Doctoral Dissertation of the Oklahoma State University，2005.

［6］ Stahl K J，White J W，Deckert K L.Dynamic Response of self－Act⁃ing Foil Bearings［J］.IBM Journal of Research and Development，1974（18）：513－520.

［7］ Adams G G.A Novel Approach to the Foil Bearing Problem［J］.Tri⁃bology and Meshanics of Magnetic Storage Systems，ASLE Special Publication，1989（26）：1－7.

［8］ Lakshmikumaran A V，Wickert J A.On the vibration of cou－pled traveling string and air bearing system［J］.Transaction of the ASME，1996（118）：398－405.

［9］ 刘延柱，陈立群，陈文良.振动力学［M］.北京：高等教育出版社，2011.

［10］ 杨育霞，许 珉，廖晓辉.信号分析与处理［M］.北京：中国电力出版社，2007.

［11］ 任玉杰.数值分析及其MATLAB实现［M］.北京：高等教育出版，2007.

The Equilibrium Analysis of Coupling System between Axially Moving Paper and Air Cushion

LI Lu－lei，CAI Zhong－qing，HUI Sheng，Xu Pei－min
（School of Mechanical Engineering，Anhui University of Technology，Maanshan Anhui 243032，China）

The sine curve gas floating dryer is widely applied to transport and dry the paper without contact in paper industry.To the extent that transverse deformation of axial moving paper couples with the air pressure in air cushion area.In order to ob⁃tain these two important process parameters in equilibrium state，it is necessary to regard the paper and air cushion as a cou⁃pling system.In the one－dimensional model considered here，the paper is approximated as an axially moving Euler－Bernoulli beam under tension，and the air pressure in the bearing region satisfies continuity equation andN－Sequation for unsteady in⁃compressible flow，the governing equations and coupling condition for the paper and the air cushion are established.The equi⁃librium pressure in air cushion area and the paper deformation are determined through finite difference method and Newton－Raphson method.Finally，the dependence of the system′s equilibrium state on the transport speed and traction tension is dis⁃cussed.

paper transverse deformation；air cushion pressure；coupling system；equilibrium state

O39

A

1007－4414（2013）04－0017－06

2013－05－28

国家自然科学基金项目（50975003）

李路雷（1989－），男，安徽阜阳人，硕士，主要从事机械动力学研究方面的工作。