无穷电阻网络的分析
2013-01-27田社平陈洪亮
田社平,张 峰,陈洪亮
(上海交通大学电子信息学院,上海 200240)
无穷电阻网络的分析
田社平,张 峰,陈洪亮
(上海交通大学电子信息学院,上海 200240)
无穷电阻网络是一类特殊的电路,它有助于学生理解电路的分析方法。根据该电路的特点,本文总结了其分析方法,包括叠加定理法、等效变换法、网孔法和节点法等,这些方法充分利用了电路的无穷性和对称性。本文的讨论对电路课程的教学具有一定的参考价值。
无穷限电阻网络;等效变换;网孔分析法
0 引言
在“电路分析”课程教学中,无穷电阻网络是一类特殊的电路,其主要特点是具有无穷性和对称性,使得其分析方法具有很大的灵活性和技巧性,从而有助于学生理解电路的分析方法。图1所示为一常见的无限方格电阻电路,其中所有电阻均为1Ω,现要求流过电压源的电流I。许多电路教材或教学参考书或文献都涉及到类似的电路[1~5]。教材中对这类电路的求解主要采用叠加定理。笔者在教学中发现,尽管利用叠加定理求解十分简洁明了,但除此之外,还可采用其他电路分析方法如等效变换法、网孔法和节点法等求解。
为方便起见,本文的讨论中,所有未标示的电阻其阻值均取1Ω。
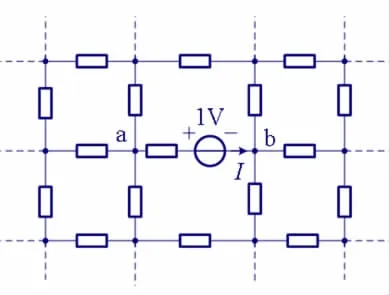
图1 无穷电阻网络
1 应用叠加定理求解
为便于比较,这里首先给出应用叠加定理的求解方法。
将含源支路等效变换为诺顿电路,如图2(a)所示。由KCL可得

为求I1,将1A电流源分解为两个1A电流源的串联,两电流源的连接点伸向无穷远处,如图2(b)所示。
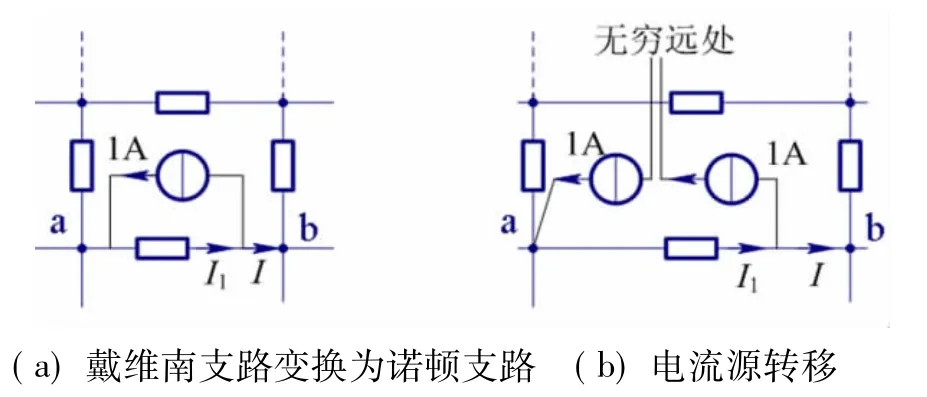
图2 利用叠加定理求解
由叠加定理可知,当左边1A电流源单独作用时,由电阻分布的对称性得到I1的分量为0.25A。同理,当右边1A电流源单独作用时,得到I1的另一分量也为0.25A,因此 I1=0.5A。由式(1)可以得到 I=I1-1=-0.5A。
上述分析方法的关键在于利用了叠加定理和电路的对称性,其解法简洁明了。这是现有教材中的通用解法。
2 应用等效变换方法求解
图1电路还可以采用等效变换的方法来分析。观察该图电路,可以看出其中任一节点都关联4个电阻,因此可将图1电路改画为如图3(a)所示的电路,该电路具有无穷和对称的拓扑结构。假设从ab两端看进去的无穷电阻网络的等效电阻为Re,则由图3(b)可得

其结果为Re=1Ω。这样图3(a)电路可简化为图3(c)所示电路,从而得出
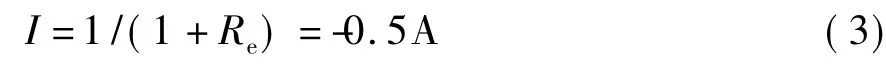
由图3(a)电路的特点,还可提出一种求解方法。由电路的对称性,可知电流I平均分配到与b点相连的3个电阻,这3个电阻的电流同样平均分配到与之相连的3个电阻,…依此类推,由KVL得
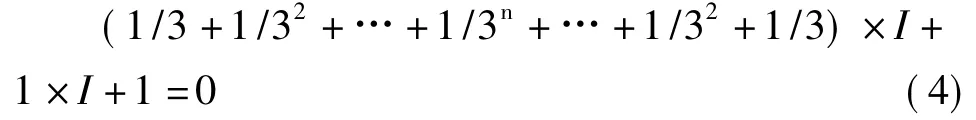
由上式同样可解得I=-0.5A。
上述分析方法的关键在于重画电路的连接方式,等效变换为一种易于分析的电路形式,其解法同样具有简洁、明了的特点。
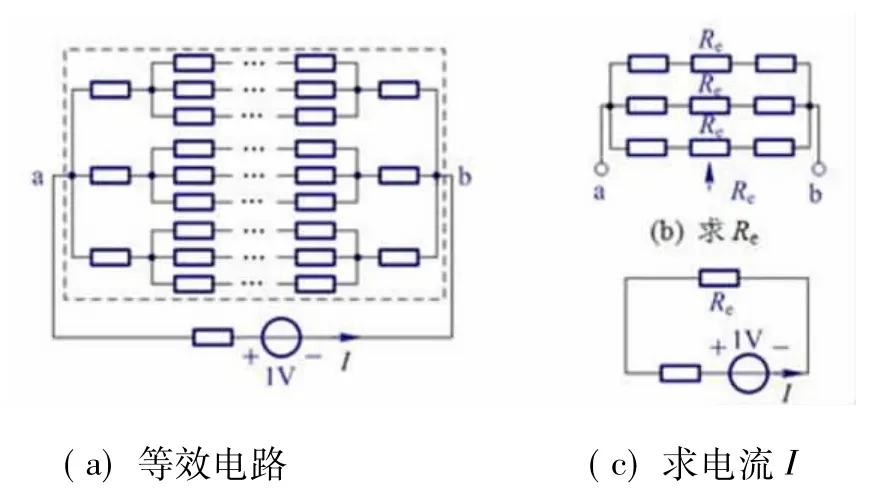
图3 利用等效变换求解
3 利用网孔法和节点法求解
图1电路为一平面电路,采用网孔法或节点法分析时,电路方程将有无穷多个,似乎无法求解。但注意到待求问题为仅需求解戴维南支路上的电流,即如果能求出与该支路关联网孔电流或该支路两端的节点电压,问题就迎刃而解。这里采用与文献[6]类似的方法即采用傅里叶变换进行分析。
采用图4所示的节点标示和网孔电流标示,假设在节点(n,p)和(n+1,p)之间的支路中接有Unp的电压源,参考方向如图中所示。对电压源下方的网孔列写网孔方程,有
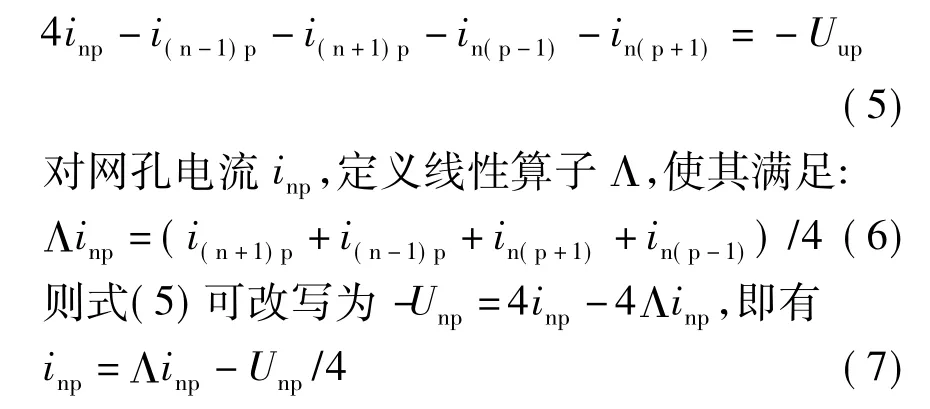
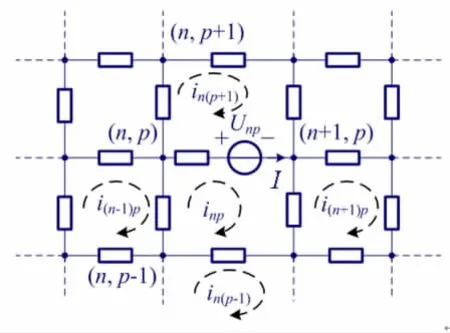
图4 利用网孔法求解
为了求解式(8),假设存在二维函数F(x,y):[π,π]×[π,π]→R,其二维有限傅里叶变换为inp,即为
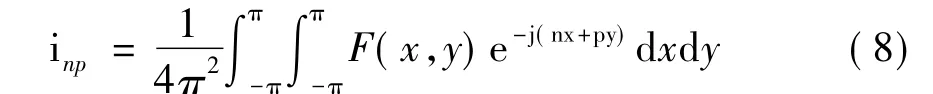
由二维有限傅里叶变换的反演公式,可得
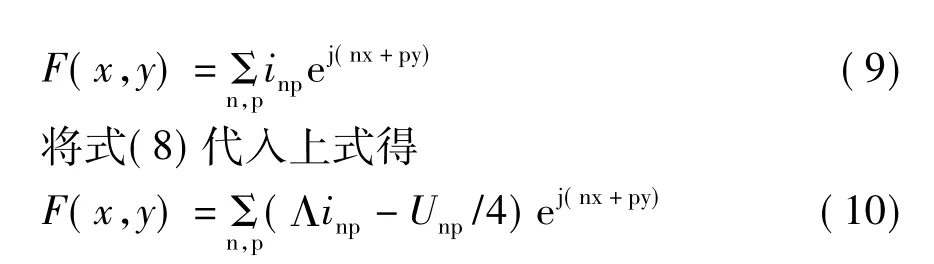
由分析的问题可知,可考虑无穷电阻网络只在节点(0,0)和(1,0)之间施加一电压为1V的电压源,参考方向如图1所示。与该电压源关联的网孔电流为i00和i01,注意到网孔电流均取顺时针方向,因此有

采用手工推导来计算上式较为繁琐,一般可借助于Matlab或Maple计算软件进行辅助计算。本文采用Maple进行计算,得到结果为I=-0.5A。
类似地,也可采用节点法进行分析,由于篇幅所限,不再赘述,这里仅给出最后结果。假设无穷电阻网络只在节点(0,0)和(1,0)之间施加1V的电压源,参考方向如图1所示,节点(0,0)和(1,0)之间的电压为

4 结语
本文讨论了无穷电阻网络的分析,拓展了其分析方法,使之更适合于在教学中加以应用。笔者在教学实践中,认为无穷电阻网络具有如下特点。
(1)趣味性—该电路是一实际中不可能存在的电路,但由于其具有无穷性和对称性的特点,使之具有较强的趣味性。在教学实际中,学生普遍对这一电路表现出浓厚的兴趣,从而提高了学好电路的积极性。
(2)分析方法的多样性和灵活性—尽管教材中一般仅给出了利用叠加定理进行分析的方法,但从本文可以看出,该电路的分析可采用多种分析方法,而且这些方法都具有一定的灵活性。
应该指出,采用网孔法和节点法的分析方法具有较强的理论性,在教学中应根据实际情况作适当处理。笔者建议网孔法和节点法的分析方法可不讲授,而作为课外拓展,以扩大学习电路的视野。
[1]李瀚荪.简明电路分析基础[M].北京:高等教育出版社.2002
[2]陈洪亮,张峰,田社平.电路基础[M].北京:高等教育出版社.2007
[3]G.Venezian.On the resistance between two points on a grid[J].Am.J.Phys.1994(62):1000 ~1004
[4]D.Atkinson and F.J.van Steenwijk.infinite resistive lattices[J].Am.J.Phys.1999(67):486 ~492
[5]陈洪亮,张峰,谢维敏等.电路基础试题集解与考研指南[M].北京:高等教育出版社.2008
[6]田社平,陈洪亮,张峰.基于Matlab的无限电阻网络等效电阻的计算[J].电气电子教学学报,2010,32(2):29-31
Analysis of Infinite Resistive Grid
TIAN She-ping,ZHANG Feng,CHEN Hong-liang
(School of Electrical and Electronic Eng.,Shanghai Jiao Tong Univ.,Shanghai200240,China)
Infinite resistive lattices are circuits with special structures.It is suitable for students to understand knowledge about circuit analysismethods.This paper has summarized analysismethods of the infinite resistive lattice according to its properties.Thesemethods have adopted substitution theorem,equivalent transform,mesh analysis and node analysiswhich fully utilize the lattice's properties of infinity and symmetry.The discussion is helpful for the teaching of circuit.
infinite resistive lattice;equivalent transform;mesh analysis
TM13
A
1008-0686(2013)01-0010-03
2012-09-05;
2012-11-15 基金项目:上海交通大学基本电路理论国家级精品课程建设项目
田社平(1967-),男,博士,副教授,主要从事电路理论和动态检测技术的教学和科研工作,E-mail:sptian@sjtu.edu.cn
