改进混合蛙跳算法优化的产品族模糊C均值聚类设计方法

崔文华， 刘晓冰， 王 伟， 王介生

（1.大连理工大学控制科学与工程学院，辽宁大连 116024；2.辽宁科技大学电子与信息工程学院，辽宁鞍山 114044）

改进混合蛙跳算法优化的产品族模糊C均值聚类设计方法

崔文华＊1，2， 刘晓冰1， 王 伟1， 王介生2

（1.大连理工大学控制科学与工程学院，辽宁大连 116024；2.辽宁科技大学电子与信息工程学院，辽宁鞍山 114044）

研究了基于改进混合蛙跳算法优化的模糊C均值聚类解决模块化产品族设计中产品平台的确定问题.建立了该产品开发过程中的部件关联矩阵，采用变个体长度的混合蛙跳算法同时优化模糊聚类数和聚类中心，求得产品构成部件的最优模糊划分.切断算子和拼接算子用来对个体进行重新组合而形成新个体，采用ISODATA迭代算法进行局部寻优.通过对纸币清分机进行的产品族设计的仿真研究，表明所提方法为产品族模块化设计提供了定量数学分析和快速配置的理论依据.

纸币清分机；产品族；产品平台；混合蛙跳算法；模糊C均值聚类

0 引 言

在国内外竞争日益激烈的市场环境当中，针对不同层次和规模的客户群体设计提供合适的金融机具产品，是金融机具企业面临的一个严重挑战.基于产品平台（product platform）的面向产品族（product family）的设计方法在产品设计中得到了广泛应用［1］，该方法扩展了面向变形的设计方法（design for variety，DFV），以提高企业的敏捷定制水平.

模糊C均值（FCM）聚类算法［2］是非监督模式识别中的一种基本方法，目前在图像处理、模式识别、模糊控制等众多领域被广泛采用.判定聚类算法是否高效需要考虑如下问题：能否自动确定聚类的数目（聚类有效性问题［3］）；是否对初始参数和噪声敏感；是否具有全局优化能力和较快的收敛速度.诸如粒子群算法［4］、微分进化算法［5］等智能优化算法被应用在模糊聚类算法中的优化领域.这些算法在某种程度上有效地克服了传统模糊聚类算法易陷入局部极小值的缺点，而且有效避免了对初始化选值敏感性的问题.另一方面，众多聚类有效性函数被提出，如Xie－Beni的Fukuyama－Sugeno的、Kwon的和 Chen－Linkens的，但基于聚类有效性函数的FCM聚类算法易陷入局部极小值和对初始化选值敏感的弱点没有得到有效解决.文献［10］则采用神经网络算法对获取最优聚类数进行了有效尝试.在面向产品族的产品开发设计领域，国内外学者采用聚类算法也进行了有效探索［1，11］.文献［1］采用模糊聚类分析方法解决饮水机的模块化产品族设计中模块和核心平台的确定问题.文献［11］采用聚类分析方法对电子产品功能模块进行提取，为产品族设计提供了一定思路.

混合蛙跳算法（SFLA）就是一种基于群体的进化搜索智能算法［12］.2009年，Amiri等［13］采用SFLA对K均值聚类问题进行了求解；杜长海等［14］提出SFLA－FCM优化交通时段划分问题，但没有考虑聚类有效性问题.

本文应用基于改进混合蛙跳算法优化的模糊C均值聚类解决模块化产品族设计中产品平台的确定问题，以期为产品族模块化设计提供定量数学分析和快速配置的理论依据.

1 FCM聚类算法

FCM聚类算法将特征空间X＝（x1，x2，…，xn）中的特征点分为c类（2≤c≤n），第i类的聚类中心用vi表示，其中任意特征点xj属于第i类隶属度uij（0≤uij≤1），且uij满足如下条件：

FCM聚类算法的目标函数［15］为

其中m＞1.FCM聚类算法的目的就是获取最小化目标函数（3）的U＝（uij）c×n和V＝（v1v2…vc）.

ISODATA算法流程如下（算法流程1）：

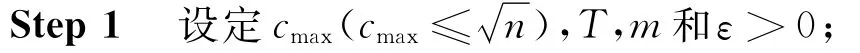
Step 2对于c＝2，3，…，cmax，初始化V0＝（v10v20…vc0）；

Step 3针对迭代次数t＝1，2，…，T，根据以下公式计算隶属度和聚类中心：

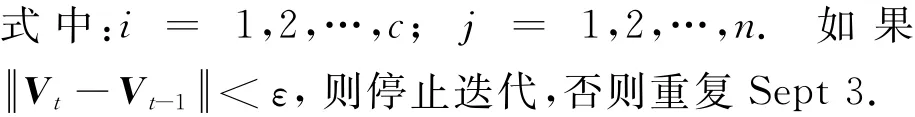
2 基于变个体长度的SFLA优化FCM参数

2.1 SFLA算法

SFLA算法的基本思想是［12］：随机生成S维解空间中由N只蛙组成的初始种群P＝｛X1，X2，…，XN｝，第i只蛙表示为Xi＝（xi1xi2…xiS）；然后将种群内个体按适应度值进行降序排列，种群中最优个体记为Xg；接下来将蛙群个体均分为m个模因组，每组有n只蛙，即N＝m×n.设蛙的集合Mk为第k个模因组，则蛙的分配过程可用下式进行描述：

记录每个模因组中最优个体和最差个体适应度为Xb和Xw，而种群中最优个体记为Xg.然后对Xw进行局部搜索，采用如下蛙跳规则进行更新：

式中：r∈［0，1］，Dmax为蛙所跳最大距离.如X′w优于Xw，则进行个体替换，如无改进，则用Xg取代Xb，根据式（7）和（8）重新进行局部搜索；如个体依然没有得到优化，则随机产生新个体替代Xw.重复上述优化过程Lmax次，进行蛙群的混洗、排序、模因组划分和局部搜索，如此反复直到定义的收敛条件结束为止，例如达到混合迭代次数Gmax.

2.2 编码和适应度函数

本文对聚类中心向量V进行编码，设n个样本要分成c类，为了合理有效地缩小SFLA的搜索空间，本文中c的取值范围为［2，cmax］（cmax≤）.根据各自的取值范围，采用浮点数编码，则一个个体I可表示为［16］

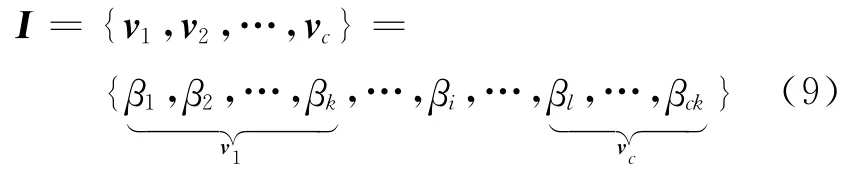
在本文中，采用SFLA对聚类中心向量V进行优化，式（9）中的聚类数c是变化的，所以个体I的长度不是固定的.本文借助Jm（U，V）定义SFLA的适应度函数：

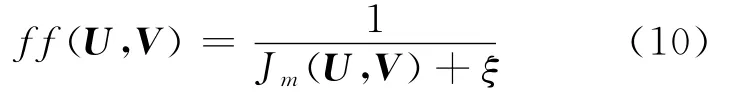
适应度函数采用如下步骤进行求解（算法流程2）：

Step 1从个体I中提取vi（i＝1，2，…，c）；

Step 2依据式（4）求取uij；

Step 3根据式（5）重新计算聚类中心参数；

Step 4根据式（3）和（10）计算ff（U，V）.确定了编码方式和ff（U，V）后，就可用混合蛙跳算法对模糊聚类数和聚类中心同时优化.

2.3 切断算子和拼接算子

由于编码方式的特殊性，由式（7）、（8）所定义的蛙跳规则不适用于变个体长度的SFLA，所以切断算子（cut operator）和拼接算子（splice operator）［16］被用来将群体中各个个体进行重组（如图1所示）.

2.4 算法流程

基于变个体长度的SFLA同时优化模糊聚类数和聚类中心的算法步骤如下（算法流程3）.

Step 1选定如下算法初始参数：N、cmax、S、m、n（N＝m×n）、Lmax和Gmax.

图1 基于切断算子和拼接算子的新蛙跳规则Fig.1 New frog－leaping rule based on cut operator and splice operator

Step 2随机生成包含N只蛙的P＝｛X1（t），…，Xk（t），…，XN（t）｝；迭代计数值t＝0；将每只蛙Xk（t）作为聚类中心参数，并根据算法流程2求出每个个体的适应度值Fk（t）＝F（Xk（t））；对蛙群按照适应度值从大到小进行排列，令Uk（t）＝｛Xk（t），Fk（t）｝和Xg（t）＝U1（t）.

Step 3根据式（1）对U进行m个模因组M1（t），…，Mj（t），…，Mm（t）的形成，令最优个体和最差个体分别为和.

Step 4对Mj（t）中的与做切断和拼接运算，产生新蛙，并采用算法流程1进行局部搜索；然后根据算法流程2，计算其适应度值，采用上文所述的蛙跳规则进行局部寻优，得到进化后的模因组M1（t）′，M2（t）′，…，Mm（t）′.

Step 5将更新后的模因组M1（t）′，M2（t）′，…，Mm（t）′内的蛙重新混合，记U（t＋1）＝（M1（t）′M2（t）′…Mm（t）′），对U（t＋1）中的蛙按照适应度值从大到小进行排列，记录Xg（t＋1）＝U1（t＋1）.

Step 6t＝t＋1，如t＜Gmax，转Step 3，否则输出最优蛙.

3 基于聚类有效性函数的模糊聚类数优化

3.1 聚类有效性函数

（1）Bezdek提出的VPC和VPE

Bezdek提出的VPC和VPE如下：

VPC在1／c和1之间有效.如果期待一个良好的划分，目标就是选取使Vpc最大的模糊划分.它最主要的优势是分配系数简便，缺点是它的单调下降，缺乏直接连接到数据本身的性能.

VPE在0和logac之间有效.对所有的概率群C，事实证明它有如下关系：0≤1－PC（C）≤PE（C）.它基本上是一个衡量模糊聚类划分的函数，与VPC类似.

（2）Xie－Beni提出的VXB

VXB是基于Jm的客观功能，通过确定平均数据和最小距离来确定聚类中心的.

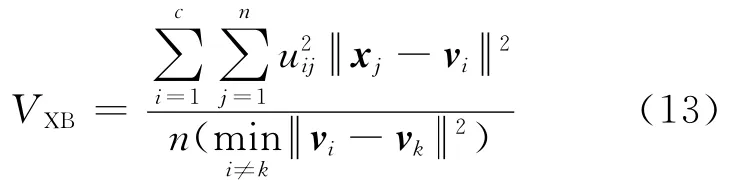
3.2 算法流程

结合FCM聚类算法和聚类有效性函数可得到最优模糊划分，其算法描述如下（算法流程4）：

Step 1指定最大聚类中心个数cmax（cmax≤），聚类有效性函数VW（U，V，c）（如式（11）～（16）），初始化T、m和ε＞0；

Step 2对于c＝2，3，…，cmax，进行V0＝（v10v20…vc0）的初始化；

Step 3针对迭代次数t＝1，2，…，T，根据式（4）和（5）计算uij，t和vj，t.如果＜ε，转下一步，否则重复Step 3；

Step 4计算VW（U，V，c）；如果c＜cmax，转步骤2；否则停止迭代，最优聚类数c＝cb，cb满足下式：

4 仿真实验

4.1 聚类有效性实验

聚类有效性准则要求模糊划分必须在紧密性和分离性间达到一定的平衡.为与基于聚类有效性函数的模糊聚类优化算法进行比较，本文采用类中距和类间距两个性能指标进行对比实验：

为了与基于聚类有效性函数对FCM算法的聚类中心个数寻优进行比较，本文采用图2中的数据集合开展研究.

表1为聚类数为2～6时，6个有效性指标在m＝2下的验证结果.从表1可以看出针对图2这个空间分布极为简单的数据集只有指标VXB、VFS和VK找到正确的模糊数4.这就说明并不是所有的有效性函数对给定的数据集均为有效.采用本文所提的基于变个体长度的SFLA－FCM算法，在10次随机运行中均得到正确聚类中心数4，并且类中距和类间距平均值分别为5.118 2和1.737 4，较好地在模糊划分的紧密性和分离性之间取得折中.

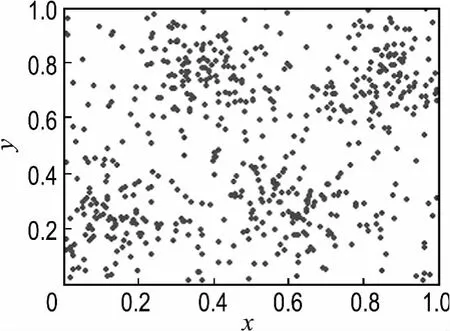
图2 具有4个聚类中心的含噪声测试数据集Fig.2 Test data set with noises having four cluster centers

4.2 基于改进的SFLA－FCM的产品族设计产品平台的选择和设计是产品族设计的核

心，其中模块化的设计涉及实现产品各项功能结构的最终整合，而在p个功能模块之间大多具有如下关系［11］：（1）每个功能模块对其余功能模块提供支撑；（2）每个功能模块从其余功能模块接受支撑.这样，任意两个功能模块之间的关系可采用p×p的模块关联矩阵进行描述.

表1 不同聚类有效性函数数据集结果（m＝2）Tab.1 Results of data set under different clustering valid function（m＝2）

本文所研究的纸币清分机是银行系统对回笼纸币进行自动清分处理的高端设备.典型纸币清分机主要功能模块有电机模块（a）、嵌入式模块（b）、网络模块（c）、操作模块（d）、直线－滚轮式走钞模块（e）、进钞模块（f）、辅助模块（g）、UV传感器（h）、磁性传感器（i）、红外光学传感器（j）、荧光传感器（k）、图像传感器（l）、测厚传感器（m）和电解质传感器（n）.

本文采用文献［11］所提的部件关联矩阵标准化处理方法对部件关联矩阵进行标准化：

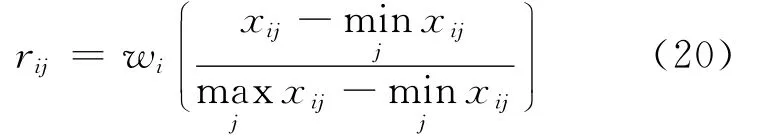
式中：maxxij和minxij分别表示某一部件同其他部件的最大和最小关联特征值；wi为功能模块i的关联权重变量.这样，对纸币清分机进行标准化处理后的模糊矩阵如表2所示.

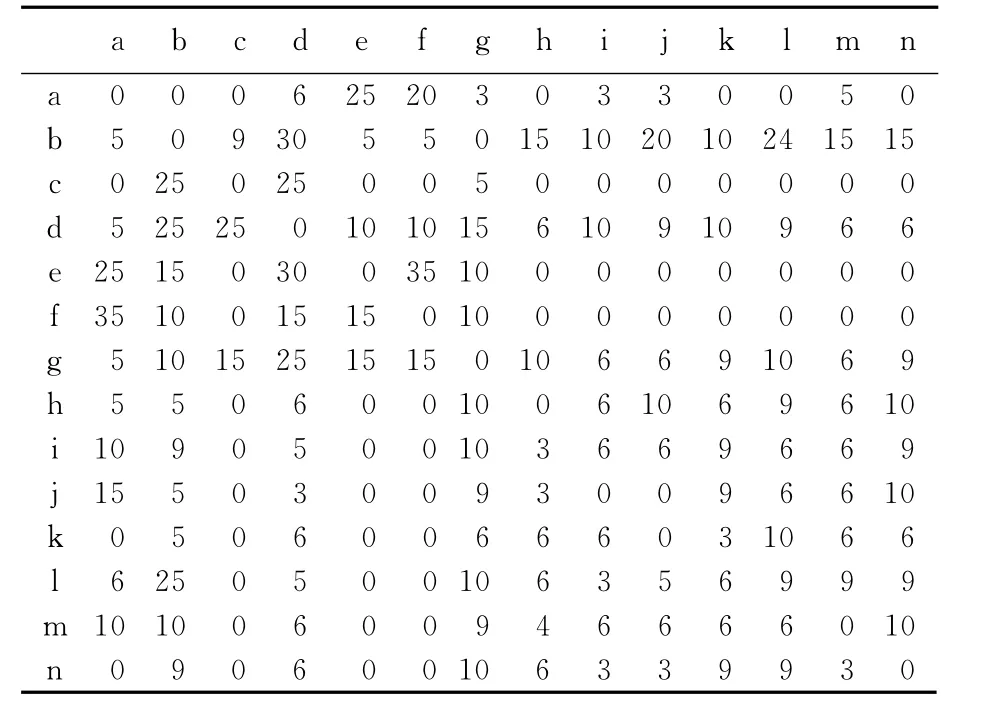
表2 部件量化后关联模糊矩阵表Tab.2 Coefficient fuzzy matrix table after component quantity

针对如表3所示的标准化后的部件关联模糊矩阵表，采用本文所提出的基于变个体长度的SFLA来同时优化FCM的聚类数和聚类中心，得到的最优聚类数为3.同时得到最优模糊矩阵U.状态变量h以相应的相对隶属度值作为权重，基于式（21）求得各个功能模块归属各个类别的特征值H（u）表，这样就得出了最优的功能模块如表4所示分类结果.

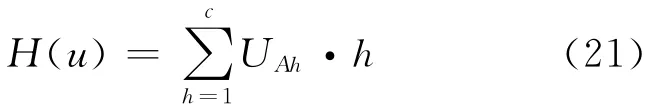
分析c＝3时的功能模块聚类结果，所研究金融机具纸币清分机的功能模块可归为3类：｛（a，e，f）；（b，c，d，g）；（h，i，j，k，l，m，n）｝.这样就可以根据金融机具生产企业的实际情况和特点，选取某些模块作为产品族设计的核心平台，例如将电机模块、直线－滚轮式走钞模块以及进钞模块等作为构成产品平台的部件.

表3 标准化模糊矩阵表Tab.3 Standardized fuzzy matrix table

表4 c为3时最优模糊矩阵和相对隶属度表Tab.4 Optimum fuzzy matrix and relative membership table under c＝3

5 结 论

（1）提出用变个体长度的混合蛙跳算法对模糊C均值聚类算法的模糊聚类数和聚类中心同时进行优化.针对FCM自身特点，采用切断算子和拼接算子对个体进行重新组合而形成新个体，然后采用ISODATA迭代算法进行个体的局部寻优以加快收敛速度.

（2）建立了纸币清分机产品开发过程中的部件关联矩阵，采用所提改进的SFLA－FCM算法来进行产品族的设计.仿真研究结果表明所提方法为产品族模块化设计提供了定量数学分析和快速配置的理论依据.

［1］Tseng M M，Jiao J X.A variant approach to product definition by recognizing functional requirement patterns［J］.Journal of Engineering Design，1997，8（4）：329－340.

［2］Arbelaitz O，Gurrutxag I，Muguerza J，etal.An extensive comparative study of cluster validity indices［J］.Pattern Recognition，2013，46（1）：243－256.

［3］Falasconi M，Gutierrez A，Pardo M，etal.A stability based validity method for fuzzy clustering［J］.Pattern Recognition，2010，43（4）：1292－1305.

［4］LI Chao－shun，ZHOU Jian－zhong，KOU Pan－gao，etal.A novel chaotic particle swarm optimization based fuzzy clustering algorithm ［J］.Neurocomputing，2012，83（15）：98－109.

［5］HE Yao－yao，ZHOU Jian－zhong，KOU Pan－gao，etal.A fuzzy clustering iterative model using chaotic differential evolution algorithm for evaluating flood disaster［J］.Expert Systems with Applications，2011，38（8）：10060－10065.

［6］XIE Xuan－li，Beni G.A validity measure for fuzzy clustering［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1991，13（8）：841－847.

［7］Fukuyama Y，Sugeno M.A new method of choosing the number of clusters for the fuzzycmeans method［C］／／Proceedings of the International Conference of the Fifth Fuzzy System Symposium.Kobe：The Japan Society of Applied Physics，1989：247－250.

［8］Kwon S H.Cluster validity index for fuzzy clustering［J］.Electronics Letters，1998，34（22）：2176－2177.

［9］Chen M Y，Linkens D A.Rule－base self－generation and simplification for data－driven fuzzy models［J］.Fuzzy Sets and Systems，2004，142（2）：243－265.

［10］Alp Erilli N，Yolcu U，E，etal.Determining the most proper number of cluster in fuzzy clustering by using artificial neural networks［J］.Expert Systems with Applications，2011，38（3）：2248－2252.

［11］王爱民，孟明辰，黄靖远.聚类分析法在产品族设计中的应用研究［J］.计算机辅助设计与图形学学报，2003，15（3）：343－347.

WANG Ai－min，MENG Ming－chen，HUANG Jingyuan.Research on clustering analysis for product family design［J］.Journal of Computer－Aided Design＆Computer Graphics，2003，15（3）：343－347.（in Chinese）

［12］Eusuff M M，Lansey K E.Optimization of water distribution network design using the shuffled frog leaping algorithm［J］.Journal of Water Resources Planning and Management，2003，129（3）：210－225.

［13］Amiri B，Fathian M，Maroosi A.Application of shuffled frog－leaping algorithm on clustering［J］.The International Journal of Advanced Manufacturing Technology，2009，45（1－2）：199－209.

［14］杜长海，黄席樾，杨祖元，等.改进的FCM聚类在交通时段自动划分中的应用［J］.计算机工程与应用，2009，45（24）：190－193.

DU Chang－hai，HUANG Xi－yue，YANG Zu－yuan，etal.Application of improved fuzzyC－means clustering in automatic programming traffic intervals［J］.Computer Engineering and Applications，2009，45（24）：190－193.（in Chinese）

［15］Kannan S R，Devi R，Ramathilagam S，etal.Some robust objectives of FCM for data analyzing［J］.Applied Mathematical Modelling，2011，35（5）：2571－2583.

［16］WANG Jie－sheng，GAO Xian－wen.Optimization of fuzzyC－means clustering by genetic algorithms based on sizable chromosome［C］／／Proceedings of 2009Chinese Conference on Pattern Recognition.New York：IEEE Press，2009：1－5.

Product family design method based on fuzzyC－means clustering method optimized by improved shuffled frog leaping algorithm

CUI Wen－hua＊1，2， LIU Xiao－bing1， WANG Wei1， WANG Jie－sheng2
（1.School of Control Science and Engineering，Dalian University of Technology，Dalian 116024，China；2.School of Electronic and Information Engineering，University of Science ＆Technology Liaoning，Anshan 114044，China）

The decision of product platform in the modularized product family design is proposed based on fuzzyC－means（FCM）clustering algorithm optimized by the improved shuffled frog leaping algorithm（ISFLA）.The component coefficient matrix based on the data collected in the product exploitation process is set up.The number of fuzzy clustering and cluster centers are optimized by sizable－individual SFLA to obtain the optimized fuzzy partition of the components of the product.Cut operator and splice operator are used to combine the individuals to form a new individual.ISODATA

iterative algorithm is adopted to carry through the local optimization.The simulation results of the product family design of the paper currency sorter show that the proposed method provides the theoretical basis of the quantitative mathematic analysis and fast configuration for the product modularized design.

paper currency sorter；product family；product platform；shuffled frog leaping algorithm；fuzzyC－means clustering

TP12

A

1000－8608（2013）05－0760－06

2012－05－09；

2013－07－20.

辽宁省教育厅创新团队基金资助项目（2008T091）；辽宁省科技攻关计划资助项目（2010220001）.

崔文华＊（1968－），女，教授，E－mail：cwh＠julong.cc；刘晓冰（1956－），男，教授，博士生导师.