基于MF-DCCA方法的证券市场间交叉相关性研究
2013-01-23曾志坚张倩倩
曾志坚,张倩倩
(湖南大学 工商管理学院,湖南 长沙 410082)*
一、引 言
2012年6月29日签署的《〈内地与香港关于建立更紧密经贸关系的安排〉补充协议九》指出“内地将支持符合香港上市条件的内地企业赴香港上市,为内地企业特别是中小企业到境外市场直接上市融资创造便利条件,同时积极研究降低香港金融机构申请合格境外机构投资者资格的有关资质要求,为香港有关长期资金投资内地证券市场提供便利”。这无疑会使得香港市场和内地市场的联系变得更加紧密。在此背景下,本文对上海证券市场和香港证券市场间的交叉相关性进行探讨,一方面有利于投资者了解证券市场间的联动关系及信息传递,为投资者做出决策提供参考意见,另一方面,对防范金融风险的传染,维护证券市场持续、健康发展也有着积极作用。
二、相关文献综述
关于证券市场间的交叉相关性,学者们最初主要运用Granger因果检验、动态条件相关模型(DCC)和Copula模型等进行研究。Parsva和Lean利用Granger因果关系检验证实了科威特等6个中东国家股票市场和外汇市场间存在因果关系[1]。Lee运用Granger因果检验和协整检验对汇改之后的中国汇率市场和香港股票市场进行分析,发现两个市场之间存在单向Granger因果关系[2]。潘越通过非线性Granger因果检验进行研究,结果表明A股和H股之间一直存在因果关系[3]。董秀良和吴仁水运用DCC-MGARCH模型,发现沪深A、B股市场的相关系数总体为正,但数值较小,并具有明显的时变特征[4]。Xiao和Dhesi利用DCC模型进行研究,结果表明英国、美国、法国和美国四个证券市场间存在显著的时变相关性[5]。Arouri和Bellalah等通过建立DCC-GARCH模型,发现1994年后哥伦比亚等新兴证券市场间的相关性显著增加[6]。王永巧和刘诗文利用时变Copula模型进行分析,结果表明中国股市与美国、英国及日本股市保持微弱的下尾相依关系[7]。曾志坚等利用时变Copula模型发现在金融危机时期,美国证券市场对中国证券市场的波动溢出效应有增强的趋势[8-10]。刘琼芳和张宗益运用Copula模型检验了房地产和金融行业股票之间的相关关系,结果表明这两个行业的股票在市场低迷时期的尾部相关性要大于在市场活跃时期的尾部相关性[11]。
以上研究采用的方法均建立在证券市场有效假说基础之上,构建的是一种线性均衡的分析范式。然而,现实的证券市场是一个复杂的动力系统,时间序列往往具有非平稳和分形特征,各时间序列之间普遍存在幂律形式的交叉相关性。上述文献中的研究方法不能很好地分析不同时间标度下时间序列的分形特征,因而无法准确描述证券市场间的交叉相关性。基于分形理论的多重分形去趋势交叉相关分析法(MF-DCCA)能够有效去除局部趋势对时间序列标度的影响,可以探测不同时间标度下时间序列所呈现的分形特征,是研究非平稳时间序列之间长期幂律交叉相关性的有效手段。因此,本文拟采用MF-DCCA方法研究上海和香港证券市场间的交叉相关性。
三、实证研究设计
(一)样本选取与数据来源
选取上证综合指数和恒生指数分别代表上海证券市场和香港证券市场的走势。由于2006年5月《上市公司证券发行管理办法》施行后,H股企业纷纷回归A股市场,到2006年12月31日,H股企业回归A股市场达到一个高潮。因此,本文选取的样本时间跨度为2007年1月3日~2013年5月31日。由于上海证券市场和香港证券市场因节假日而休市的日期有所不同,故删除时间不一致的记录,最终得到1510个样本数据。数据来源于国泰安数据库(http://www.gtarsc.com/)。本文采用各市场的日指数收益率数据进行研究,其计算公式如下:
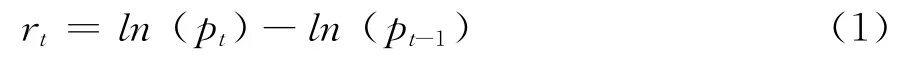
其中,rt为t时刻的收益率,pt和pt-1分别是t和t-1时刻的收盘价格。
(二)实证研究方法
首先检验上海和香港证券市场之间是否具有交叉相关关系,再运用MF-DCCA方法研究两市场间的交叉相关性及分形特征。
1.交叉相关性检验方法。对于两个时间序列{xt,t=1,2,…..N}和{yt,t=1,2,…..N},定义其交叉相关函数为:
交叉相关统计统计量为:
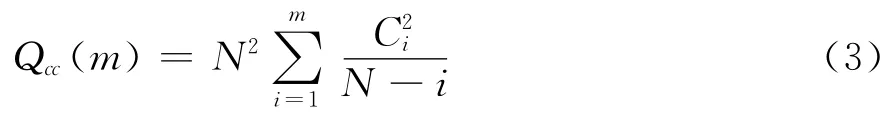
其中m是自由度,交叉相关统计量Qcc(m)则近似于自由度为m的卡方分布χ2(m)。
2.MF-DCCA方法。(1)假设两个时间序列{x(i)}和{y(i)},i=1,2,..N,N是时间序列的长度,构造新的时间序列:


(2)把时间序列{x(i)}和{y(i)}分成Ns=int(N/s)个不相重叠的子区间,每个子区间的长度为s。因为长度N可能不是子区间长度s的整数倍,为了能保证序列结尾的N-Ns×s的值也考虑在内,对时间序列的逆序做同样的处理。这样就可以得到2Ns个子区间。
(3)在每一个子区间v中,通过最小二乘法用多项式函数xv和yv拟合轮廓,对于v=1,2,……Ns,局部协方差函数为:

对于v=Ns+1,……2Ns,局部协方差函数为:
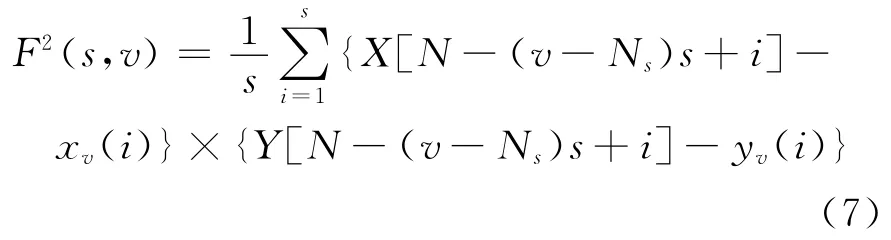
(4)把所有子区间的局部协方差取均值,可得到q阶波动函数:

一般来说,q可以是非零的任意实数。当q=0时,由洛必达法则得:

(5)计算不同标度s所对应的波动函数Fq(s)。如果两个序列之间存在长期幂律交叉相关性,则波动函数Fq(s)和时间间隔s存在以下标度关系:

其中,标度指数Hxy(q)即为广义赫斯特指数,是ln(Fq(s))~lns函 数 关 系 图 的 斜 率。通 过MF-DCCA得到的广义赫斯特指数Hxy(q)与多重分形标度指数τ(q)关系如下:

通过Legendre变换,可以得到描述多标度时间序列的多重分形谱f(α):

其中,α为奇异指数,用来描述时间序列的奇异程度。f(α)为多重分形谱,它的值反映了具有奇异指数α的分形维数。
四、实证结果分析
(一)交叉相关性检验结果分析
首先验证上海和香港证券市场间是否存在交叉相关关系。自由度m的取值范围是从1~1000,对于不同的自由度m,分别计算其相应的交叉相关统计量Qcc(m)和卡方分布χ2(m)的临界值。

图1 交叉相关性检验Qcc(m)
图1中实线表示交叉相关性统计量Qcc(m),虚线表示自由度为m,显著性水平为5%时卡方分布x2(m)的临界值。从图中可以看出,在自由度从1~1000范围内,交叉相关性统计量Qcc(m)均大于相应的卡方分布x2(m)的临界值,这表明上海和香港证券市场之间存在显著的交叉相关性。
(二)MF-DCCA结果分析
进一步利用MF-DCCA方法准确量化上海和香港证券两个市场之间的交叉相关性,设定时间标度s的取值范围是从10~N,N为时间序列的长度,q的取值为q=5,4,……-4,-5。

图2 上海与香港股票市场收益率序列的双对数波动曲线图
从图2可以看出,对于不同的q,其波动函数Fq(s)和时间标度s之间都表现出较好的幂律关系,即上海和香港证券市场之间存在着交叉相关性。这表明上海证券市场波动的变化不仅受到自身波动的影响,也会受到香港证券市场波动的影响;而香港证券市场的波动也会受到上海和香港两个证券市场的影响。
通过最小二乘法拟合得到上海和香港证券市场收益率序列双对数波动曲线ln(Fq(s))~lns函数关系图的斜率Hxy(q)(参见表1)。

表1 股指收益率的Hxy(q)指数
由表1可以看出,当q从-5变化到+5时,两个证券市场的交叉相关指数Hxy(q)从0.5969递减到0.4193。Hxy(q)是随着q的变化而变化,不是一个固定的常数,这说明上海证券市场和香港证券市场之间的交叉相关性具有多重分形特征。这也证明了两个证券市场间的关系是非线性的,采用正态分布、单重分形等传统方法对这两个市场之间的关系进行描述是不合适的,因此。需要突破传统的线性范式,以非线性的角度来分析证券市场中的问题。因此不论是投资者还是监管者都应该将这两个市场当作一个整体来考虑,仅仅考虑其中一个市场,而忽略另外一个市场,会导致对证券市场的理解产生偏差。
产生多重分形的原因主要来自两个方面:一是由于证券市场上存在的长程相关性;二是由于证券市场时间序列的厚尾分布。长程相关性表明证券市场上出现的波动会影响未来证券市场价格的变化趋势,市场上可能会出现连续的上涨和下跌。从表1可以发现,当q=2时,Hxy(q)=0.5055>0.5,说明上海和香港两个证券时间之间存在长程相关性,一个市场的价格对另一市场的历史价格具有长期记忆性,即一个证券市场上出现的波动会对另一个市场的未来收益产生影响。
时间序列的厚尾分布说明,上海和香港两个证券市场既不像有效市场假说所阐述的大幅波动出现的概率几乎为零,也不像单一分形所描述的大幅波动和小幅波动出现的概率几乎相等,而是不同幅度的波动具有不同的标度关系,即大幅波动和小幅波动出现的概率以及具有的风险程度都是不同的。投资主体对成堆信息的非线性处理方式将导致厚尾分布的出现。一般而言,当颁布某项新政策时,大部分投资者不会及时地对此做出反应,只有当信息累积到一定程度,才会做出决策。这就使得市场上出现的信息不能立即被投资者消化,相反会形成某种程度的累加效应,导致“羊群效应”、“追涨杀跌”等现象的出现。
从图3可以看出,当q<0时,上海和香港证券市场之间的交叉标度指数要小于两个市场的平均标度指数,即两个市场的交叉相关性要小于其自相关性。而当q>0时,上海和香港证券市场之间的交叉标度指数要大于两个市场标度指数的均值,即两个市场的交叉相关性要大于其自相关性。这就说明短期内当某一个市场出现较大波动时,很可能是由于另外一个证券市场的动荡所引起的,而不是因为市场自身原因所引发的。比如在由美国次贷危机引发的全球金融危机中,由于香港证券市场开放程度较高,受到严重影响,股价大跌,出现大幅波动。而香港市场和大陆市场之间的联系紧密,使得危机进一步传染到了上海证券市场,从而引发了上海证券市场的波动。
进一步依据式(11)~(13)分析上海证券市场和香港证券市场间交叉相关性的多重分形特征。为了能更清楚地描述不同q值下标度指数τ(q)的变化过程,将q值的范围放大,选取-100≤q≤100,步长为10。
从图4可以看出,标度指数τ(q)是关于q严格单调递增的凸函数,τ(q)与q之间存在明显的非线性关系。这再次表明上海和香港证券市场市场间交叉相关性存在多重分形特征。

图4 上证指数和恒生指数收益率τ(q)与q关系图

图5 上证指数和恒生指数收益率f(α)与α关系图
图5是多重分形谱f(α)与奇异指数α关系图。从整体来看,f(α)曲线顶部较平坦,开口宽大,曲线分布在较大的范围内。从具体数值来看,f(α)在α等于0.276885时达到最小值0.2879,在α等于0.5363时达到最大值1,f(α)是随着奇异指数α值的变化而变化。多重分形谱中奇异指数α的最大值为0.619135减去最小值0.276885,即得到多重分形谱宽度Δα=0.343113。同标度指数τ(q)曲线结果一样,这也进一步表明了上海和香港证券市场的交叉相关性具有多重分形特征。
五、结 论
以上运用MF-DCCA方法进行研究,发现上海和香港证券市场之间存在显著的长程交叉相关性,且呈现出多重分形特征。一方面,说明上海和香港证券市场不仅会受到市场自身的波动而发生变动,还会受到彼此波动的影响。另一方面,表明投资者是以非线性的方式对市场信息做出反应,只有当信息累积到一定程度时,才会对信息进行处理,从而导致“羊群行为”等非理性行为的发生。因此,对投资者而言,在进行决策过程中,应该把上海证券市场和香港证券市场当作一个整体,全面考虑两个证券市场出现的波动对未来收益的影响,更好地规避投资风险。对金融监管者而言,同时,也应该加强对上市公司信息披露的监管,减少信息的不对称性,不断提高市场运行效率。同时也应加强对投资主体的理性投资教育,优化投资者结构,改善市场投资主体的构成,发挥机构投资者的理性投资作用,促进证券市场的长期健康发展。
[1]Parsva P,Lean H H.The analysis relationship between stock prices and exchange rates:evidence from six middle easter financial markets[J].International ResearchJournal of Finance and Economics,2011,(66):157-171.
[2]Lee W C.A Study of the causal relationship between real exchange rate of Renminbi and Hong Kong stock market index[J].Modern Economy,2012,(3):563-566.
[3]潘越.基于非线性Granger因果检验的股市间联动关系研究[J].数量经济技术经济研究,2008,(9):87-100.
[4]董秀良,吴仁水.基于DCC-MGARCH模型的中国A、B股市场相关性及其解释[J].中国软科学,2008,(7):125-133.
[5]Xiao L,Dhesi G.Volatility spillover and time-varying conditional correlation between the European and US stock markets[J].Global Economy and Finance Journal,2010,3(2):148-164.
[6]Arouri M E H,Bellalah M,Nguyen D K.The comovements in international stock markets:new evidence from Latin American emerging countries[J].Applied Economics Letter,2010,(17):1323-1328.
[7]王永巧,刘诗文.基于时变Copula的金融开放与风险传染[J].系统工程理论与实践,2011,31(4):778-784.
[8]曾志坚,徐迪,左楠.金融危机对证券市场波动溢出的影响研究[J].财经理论与实践,2011,32(174):48-52.
[9]曾志坚,范丽,周竞东.基于互谱分析的权证与标的证券收益率波动溢出研究[J].财经理论与实践,2010,(6):38-43.
[10]曾志坚,钟紫璇,曾艳.中国创业板和主板市场间溢出效应分析[J].财经理论与实践,2012,(6):43-47.
[11]刘琼芳,张宗益.基于Copula房地产与金融行业的股票相关性研究[J].管理工程学报,2011,25(1):165-1689.
