基于系统整体性的商业银行系统重要性评估方法
2013-01-23彭建刚马亚芳
彭建刚,马亚芳
(1.湖南大学 金融与统计学院,湖南 长沙 410079; 2.湖南大学 金融管理研究中心,湖南 长沙 410079)*
一、引 言
在美国次贷危机中,由单家金融机构的风险暴露造成整个金融系统的剧烈波动,引发了对系统重要性金融机构的高度关注。对花旗银行的大规模救助、华盛顿互助银行的破产等事件使得各国监管者开始重视加强对系统重要性银行的监管。系统重要性银行一般呈现业务规模大、组织和业务结构复杂程度高、负外部效应显著的特征,其个体发生的风险事件会通过金融网络给该银行所在地区甚至全球的金融体系带来大的冲击,使得金融体系无法正常运转。
针对这一问题,2011年以来,金融稳定理事会(FSB)和巴塞尔委员会(BCBS)先后共同起草发布了《全球系统重要性银行的评估方法和附加损失吸收能力要求》、《强化系统重要性金融机构监管强度和有效性》、《国内系统重要性银行治理框架》等一系列重要文件,从风险防范和风险处置等方面研究制定了针对系统性风险的政策措施。中国银监会2011年颁布了《中国银行业实施新监管标准指导意见》,该《指导意见》除对系统重要性银行提出了1%的附加资本要求外,还对系统重要性银行提出了更为严格的审慎监管要求。这些新的监管构架能够实施的前提是能够对系统重要性银行进行界定。
虽然BCBS已于2011年11月和2012年11月两次公布全球系统重要性银行名单,BCBS还将于2017年11月前根据积累的数据对评估方法进行必要修改[1],说明系统重要银行的评估方法尚未最后确定下来。
为了防范系统性风险,有必要建立整体性监管制度。整体性即指银行业的整体效应不等于各银行业机构效应之和,相对于各银行业机构的效应及其简单总和而言,银行业整体的效应会发生质变;在研究银行业系统性风险防范时,应充分考虑整个金融体系内部的相互作用和金融体系与社会的相互作用[2]。由于系统与外部环境的相干性,系统外部风险因子的冲击可能引发系统中各银行发生违约(default)。由于系统内各银行的内在相关性,可能几家银行同时发生违约,这些违约的银行成为系统性风险的传染源;系统内其他银行可能受到传染发生违约,进而在系统中将风险放大。在这一风险形成和放大的过程中,不仅对存款客户造成损失,也会对系统内的其他银行造成损失。基于这一思路,下面将从系统整体性出发,提出一种商业银行系统重要性评估方法。
二、相关研究综述
在已有的银行系统重要性的定量评估方法中,从不同的视角可以有多种分类方法,监管部门和金融机构可根据需要选取适当的评估方法。经过对已有的相关文献进行分析比较,可按照自上而下和自下而上两种不同分析途径对现有的银行系统重要性评估方法进行分类。自上而下方法是银行系统发生极端损失时,分析其中各单家银行对系统性风险所做的贡献。这一方法是按照单家银行对系统性风险的贡献确定其系统重要性。自下而上方法则是一家银行发生极端损失时,分析其整个银行系统受此影响所发生的损失。这一方法是根据单家银行对系统性风险的影响程度确定其系统重要性。由于银行业机构之间的相关性,一家银行出现问题的同时,很可能有另外几家银行也出现了问题,此时系统所受到的影响是这些问题银行共同作用的结果,而不是其中一家银行单独作用的结果,若采用自下而上的方法,很可能会将一家银行对系统的影响不适当地放大。因此,本文拟采用自上而下的方法开展商业银行系统重要性评估方法研究。
Huang等以及Lahmann和Kaserer计算了当银行系统发生极端损失时各银行对系统风险保险额度的边际贡献来度量各银行的系统重要程度[3-5]。Acharya等以及Bownlees和Engle研究了当整个银行业作为整体资本不足或平均收益下降到某个既定水平时,单家银行的预期资本短缺额,用其度量各银行的风险贡献[6,7]。他们的研究都考察了环境变化对银行业系统内要素的影响,但对银行业系统内的相关性未予考虑。
2012年,美国加州大学洛杉矶分校教授Lloyd Shapley因为在“稳定配置的理论和市场设计中的实践”研究领域的杰出贡献,于2012年获诺贝尔经济学奖。近年来,他提出的夏普利值在商业银行管理领域逐渐得到了应用。Drehmann等利用夏普利值提出了一种商业银行系统重要性评估方法[8]。在分析银行间的相互作用时,仅仅考察了某一银行是否会通过传染造成其他银行发生违约,而对其他银行遭受的损失未作考虑。其分析过程不能较好地体现银行系统内部因素的相互作用,且其计算方法容易造成银行系统重要程度与银行规模的线性关系,不能充分反映银行间的关联性和复杂性对系统重要程度的影响。贾彦东采用银行间支付结算数据,利用夏普利值对中国主要银行的系统重要性水平进行了评估,其研究工作对风险在银行间的传播进行了有价值的分析,但对银行业系统外部的冲击未作考虑[9]。
我们曾采用夏普利值确定各商业银行的风险贡献,进而将风险贡献运用到经济资本的配置中[10],该研究的目标是从微观审慎管理整体最优的角度确定单家商业银行各分支机构的风险贡献和经济资本限额,没有在宏观审慎管理层面上考虑银行间以及银行业系统与外部环境的相互作用。本文拟在上述工作的基础上,从系统整体性出发,研究在外部冲击和商业银行系统内部传染共同作用下,其存款客户和相关银行遭受的损失,并根据这两方面的损失运用夏普利值计算各商业银行对系统性风险的贡献,从而对商业银行的系统重要性进行评估。
三、评估方法的设计
(一)理论基础及相关假设
依据系统整体性的理念,系统外部的冲击和系统内部的相互作用是系统性风险的诱因。在分析银行业系统性风险时,考虑商业银行两种情形的“违约”(本文指银行资不抵债的情况),第一种情形是由于系统外部风险因子冲击使得银行资产价值发生变化,导致商业银行资不抵债,发生“基础性违约”;第二种情形是由于系统内一些商业银行发生违约,使得其他商业银行无法足额回收同业资产,导致其资不抵债,此类违约为“传染性违约”。在一个开放的商业银行系统中,一旦系统中有银行发生基础性违约,风险便在系统内传染,发生传染性违约,直到没有新的银行违约为止;此时可通过计算整个基础性违约过程和传染性违约过程中存款客户及相关银行遭受损失之和,来表示系统性风险的大小。
为方便分析,将银行的资产负债结构简化为表1所示的几个部分。

表1 商业银行资产负债构成
其中,IBAi表示银行i的同业资产,OAi表示商业银行i的总资产扣除同业资产之外的其他资产,IBLi表示银行i的同业负债,OLi表示商业银行i总负债扣除同业负债之外的其他负债(为便于说明,用存款代称该部分负债,OLi的债权人用存款客户代称),Ki表示银行i的所有者权益。并且假设银行i的负债结构不变。
(二)模型
一家银行的资产会受到诸如宏观经济条件、行业风险等因素影响。假定银行i的资产收益服从均值为μi,方差为σVi的正态分布,dzi是维纳过程,则银行i的资产价值Vi满足下式:

在考察期内任意时刻t银行i的资产价值Vi服从对数分布。若初始时刻银行i的资产价值为,根据引理,则在时刻t银行i的资产价值可表示为:

其中,Zi~N(0,1)进一步将Zi分解为Zi=为共同风险因子,可视为宏观冲击因子,ρi为共同因子载荷且ρi∈[0,1],表示各银行与共同风险因子M的相关程度。Xi为银行i的特质风险因子,且M,Xi为独立同分布的服从标准正态分布的随机变量。
根据前文假设,在考察期内0~t时刻,银行的负债总额及负债结构不变,模拟各个银行资产价值变化,若模拟结果得到:
Vi=OAi+IBAi≥OLi+IBLi,则银行i是正常经营的。相反,若Vi=OAi+IBAi<OLi+IBLi,则银行i发生基础性违约。
设银行i持有的银行j的资产为xji,那么,银行i持有同业的资产,即其同业负债共为。令表示银行j借给银行i的资产占银行i的同业负债的比例,则银行i的基础违约还可表示为:
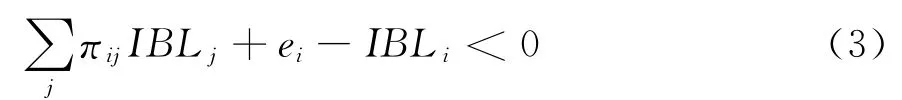
其中,π为n×n矩阵,e=(e1,…,en)表示在时点t各银行偿还了存款客户(OLi的债权人)之后,可用于银行间支付的剩余价值,其中:ei=Vi-IBAi-OLi=OAi-OLi。
系统中一旦有银行发生基础性违约,则系统内部开始清算,系统内的清算规则及清算过程参考Eisenberg与Noe(2001)[11]。清算最重要的一条原则是优先偿还存款客户的债务,银行发生违约时,银行的资产(包括从同业回收的资产)应优先偿还给存款客户。
利用Eisenberg &Noe(2001)的研究成果,系统稳定时(没有更多的银行再陷入违约),各银行清算支付向量的求解可转化为下面的线性规划问题的求解:


其中,p=(p1,…,pn)表示系统内清算的支付向量,f(p)为关于pi(i=1,…,n)单调递增的线性函数,IBL=(IBL1,…,IBLn)。若 给 定f(p)=,上述线性规划问题就是求解极值问题,即在满足支付条件约束下,要求系统内银行最大程度地偿还同业间债务。容易知道,系统稳定时银行的清算支付向量应满足:
其中表示银行i在系统清算时实际支付给其他银行的额度。式(5)表示银行i能全额偿还其同业债务;式(6)表示银行i只能偿还部分同业债务;式(7)表示银行i不能偿还其同业债务。
(三)系统内部脆弱程度指数
求解清算支付向量之后,可立即判断出i是否因传染发生违约。
容易知道,当银行i的情况是式(3)情形时,银行i发生了基础性违约。若:

同时成立,则银行i发生传染性违约。传染性违约意味着银行自身是稳健的,但由于系统内部的相互作用变得资不抵债。
对各家银行发生基础性违约和传染性违约的次数进行统计,分别用和表示各家银行发生基础性违约和传染性违约的次数。据此构造出一个表示各银行在系统内脆弱程度的指数,该指数表示银行i受到其他发生基础性违约的银行影响进而发生传染性违约的可能性。βi越大,说明银行i越容易受到其他银行影响发生传染性违约,银行在系统内部越脆弱,越应该注意防范传染风险。
(四)系统性风险的测算
下面对整个过程中形成的损失进行分析。显然,只有当银行发生违约时才会形成损失。结合式(3)、式(8)、式(9)可判断银行是否发生违约。
若银行i发生违约,依据清算中优先偿还存款客户的规则,OAi与从同业回收的资产都应优先用来偿还存款客户。所以,若银行i的OAi与之和大于OLi,则能还清对存款客户的债务;否则,会对存款客户造成损失,综合起来,对存款客户造成的损失可表示为:


那么,整个过程形成的总损失为:

用这个损失值来表示系统性风险的大小。L越大,系统性风险越大,当L大于某个阈值LVaR时,认为发生了极端的系统性风险事件。
本文对两种违约的判断与Drehmann相同,但在计算损失时,Drehmann假设一旦银行i违约,其造成的损失为OLi×Ii×LGD,这种处理方法对损失的计算比较粗糙,且忽略了违约银行对其相关银行造成的损失,这样的简化计算不是很合理,因此,以下将结合系统性风险贡献的计算给出详细分析。
(五)用夏普利值计算风险贡献
在定义了系统性风险事件之后,用夏普利值计算各家银行的系统性风险贡献。设系统N包括n家银行,系统内银行i的夏普利值的一般形式为:
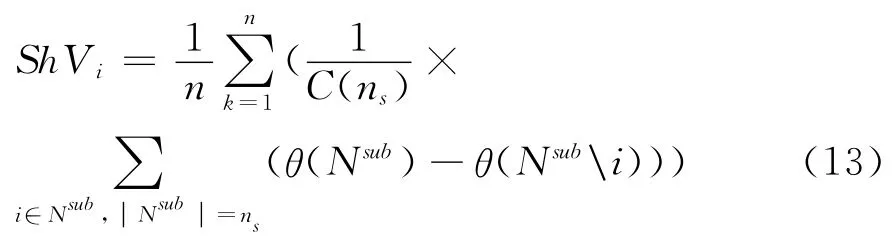
其中,ns表示系统N内银行子组合Nsub中银行的个数,C(ns)表示包含ns家银行的所有银行子组合形成的集合,θ表示特征函数。
结合具体问题,定义特征函数θ为系统对整个经济体系造成的损失L。因此,本文的夏普利值表示为:
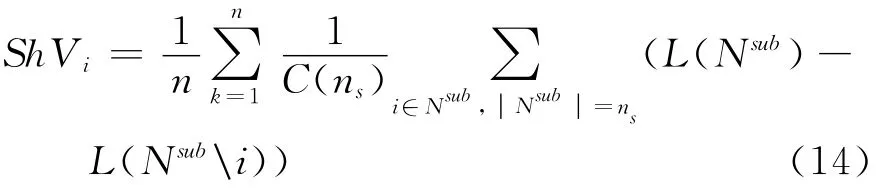
这表示,银行i的风险贡献是第i家银行对所有包含它的组合Nsub的边际风险贡献的期望值。结合前文对系统性风险事件的定义,进一步得到:


其中,j,Lj>LVaR表示只计入满足约束Lj>LVaR的事件,表示满足约束的事件次数。若定义LVaR为L的某个分位数Lq时,根据,式(15)就等价为:

最终,用式(16)计算各银行的系统性风险贡献。
结合式(16)分析计算总损失时加入对相关银行造成损失的必要性。若只考虑对系统外非银行存款人造成的损失,式(16)可表示为:
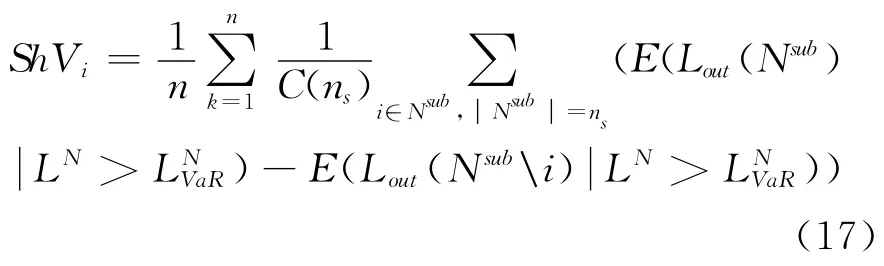
当所考查的事件是极度极端事件时,按照Drehmann的方法计算,则:

Ii是银行i违约与否的示性函数。此时,第i家银行的夏普利值等于OLi×Ii×LGD。也就意味着,在极端情形下,Drehmann的方法得到的银行系统性风险贡献是银行的存款规模的线性函数,这种结果不能体现银行间的关联性和复杂性等其他方面对其系统重要程度的影响。若加入对相关银行的损失则可以避免这一问题。
四、实证研究及结果分析
(一)数据说明
考虑到数据的可得性以及计算条件的限制,选取我国上市银行中的10家(其中,由于农业银行2009年和2010年尚未上市缺相关数据,故只在2011年的分析中将其加入)作为研究对象,采用样本银行的年报数据和股票价格数据,对其2009~2011年的系统重要性进行分析。各银行数据来自国泰安数据库。在实证过程中,利用各年度相关数据,利用默顿模型重复模拟银行资产价值,得到各年度10000次系统发生损失的事件。
(二)系统内部脆弱程度指数估计
根据计算过程中数据整理得到表2。以招商银行为例,对表2各项进行简单说明:kdf表示在2009~2011年的模拟计算过程中,招商银行平均发生了1359次基础性违约,而其因受到其他8家银行的基础性违约的影响,平均发生了2887次传染性违约。从表2所列的结果来看,工商银行β值最低,所以该银行在系统内部也最为稳定,其系统内部脆弱程度较低,系统内的相互作用对工商银行的影响最小。此外,兴业银行、南京银行、北京银行、中信银行的β最高,说明这些银行更容易受到系统内其他银行的影响发生违约,这些银行要格外注意控制传染性风险。

表2 样本银行系统内脆弱程度指数
(三)系统性风险贡献占比及系统重要性排名
根据各年度数据重复模拟计算得出的10000个系统损失的99.5%分位数来界定系统性风险事件。再利用夏普利值计算各家银行的系统性风险贡献。经过测算,主要结果列出见表3。

表3 2009~2011年样本银行风险贡献占比及系统重要性排序
对表2中的计算结果分析如下:从2009年、2010年的结果来看,中国银行、工商银行、建设银行比其他几家银行(因农业银行2010年上市,故2009年和2010年没有对农业银行进行排名)更凸显其系统重要性。2011年,中国银行、农业银行、工商银行和建设银行四家银行的系统性风险贡献占比之和达到了70%之上,说明我国银行业的系统性风险比较集中,“大而不能倒”的现象在我国是存在的,监管部门应当密切关注这一问题,采取措施控制大型商业银行的风险溢出效应。
从表3的数据可以发现,银行的系统重要性不仅仅与其规模有关,如中国银行的资产规模不及建设银行,但其2009年和2011年的系统重要程度均高于建设银行。产生这一现象的原因,可能是由于中国银行的同业业务占比较高,而建设银行的同业业务占比相对较低②,中国银行在系统内与其他银行的关联更为紧密,故中国银行的系统重要性更强。
应注意的是,2009~2011年商业银行的系统重要性排名在不断发生变化。因此,监管机构要适时调整更新系统重要性银行名单。
五、结 论
1.以上提出了基于系统整体性的银行系统重要性评估方法,并运用该方法测算银行系统重要性受银行规模大小和该行与其他银行之间关联程度的双重影响。这一方法解决了Drehmann方法造成系统重要性与银行规模呈线性关系的问题。
2.对监管机构而言,不仅要确定科学的系统重要性,银行评估方法还要正确把握影响系统重要性的关键因素,在识别系统重要性银行的基础上,根据影响系统重要性的关键因素制定具有针对性的政策,将银行的风险集中度把握在可控范围内。
商业银行可根据那些影响系统重要性的关键因素适当调整业务结构来降低其系统重要性程度,以避免受到更多监管要求的约束。
3.内部脆弱程度指标能反映银行间风险传染效应对单家银行的影响程度。商业银行对系统性风险的贡献体现了单家银行对银行体系的影响,而系统内部脆弱程度指标能反映银行体系对单家银行的影响,两者结合能较全面地体现单家银行和银行体系之间风险的相互作用。相对于大型国有商业银行而言,股份制银行和部分城市商业银行的内部脆弱程度指标较高,这反映了这些银行在应对风险传染时的抵御能力较弱。鉴于此,监管机构应当关注那些容易受到系统重要性银行风险溢出效应影响的银行,引导这些银行增强其在系统内部的抗风险能力。
注释:
①kcf是银行i在所有银行子组合(Nsub)中发生传染性违约的总次数的平均值,因此,出现了某些银行的kcf>10000的情况。
②2009年和2011年中国银行、建设银行的同业资产占样本银行同业总资产的比分别为38.29%、26.53%,8.85%、10.4%。2009年和2011年中国银行、建设银行的同业负债占样本银行同业总负债的比分别为20.82%、22.02%,16.77%、14.36%。
[1]陶玲.系统重要性金融机构风险防范标准[J].中国金融,2012,(2):79-80.
[2]彭建刚.基于系统性金融风险防范的银行业监管制度改革的战略思考[J].财经理论与实践,2011,32(1):2-6.
[3]Huang X,Zhou H,Zhu H B.A framework for assessing the systemic risk or major financial institutions[J].Journal of Banking &Finance,2009,(33):2036-2049.
[4]Huang X,Zhou H,Zhu H B.Systemic risk contributions[J].Journal of Financial Services Research,2012,(42):55-83.
[5]Lahmann W,Kaserer C.Measuring systemic risk and assessing systemic importance in global andregional financial markets using the ESS-indicator[J/OL].http://papers.ssrn.com/s ol3/papers.cfm?abstract_id=1906682,2011.
[6]Acharya V,Pedersen L H,Philippon T,Richardson M P.Measuring systemic risk[J/OL].http://papers.ssrn.com/sol3/papers.cfm?abstract_id=1595075##,2010.
[7]Brownlees C T,Engle R F.Volatility,correlation and tails for systemic risk measurement[J/OL].http://papers.ssrn.com/sol3/papers.cfm?abstract_id=1611229,2012.
[8]Drehmann M,Tarashev N.Measuring the systemic importance of interconnected banks[J/OL].http://papers.ssrn.com/sol3/papers.cfm?abstract_id=1859244,2011.
[9]贾彦东.金融机构的系统重要性分析——金融网络中的系统风险衡量与成本分担[J].金融研究,2011,(10):17-33.
[10]彭建刚,吴云,马亚芳.基于一致性原理的商业银行经济资本配置方法[J].系统工程理论与实践,2013,33(2):338-344.
[11]Eisenberg L,Noe T H.Systemic risk in financial systems[J].Management Science,2001,47(2):236-249.
