一种基于ORAM的数据可恢复性证明与访问模式的隐藏*
2013-01-18李红卫叶飞跃
李红卫 ,叶飞跃 ,陈 丹
(1.江苏理工学院计算机工程学院 常州 213001;2.江苏理工学院云计算与智能信息处理常州市重点实验室 常州 213001)
1 引言
云计算的发展极大地满足了客户对计算的需求,云存储的应用使得用户可以将数据存储在云中,以一种灵活、按需的方式使用和管理云中的数据。云存储的使用不但减轻了用户对存储管理的负担,而且对数据的访问不再受限于地理位置,并可降低硬件、软件、人力资源等方面的投资成本[1]。但云存储的安全性与可靠性仍是制约云存储服务快速发展的关键问题。这主要体现在两方面:一是云服务提供商(cloud service provider,CSP)能否有效地保证数据的完整性。例如,由于管理不当或设备故障造成数据损坏或丢失时,CSP能否尽快恢复数据。二是来自敌手的攻击,敌手可以通过某种途径篡改数据,CSP能否及时发现并恢复数据。另外,敌手还可以从用户访问数据的模式中间接地获知用户的操作信息[2]。例如,敌手获知用户对数据的访问为某一序列时将做出某项决策,当类似的访问序列再次出现时,敌手可以推测到用户的活动。本文从云存储中数据的可恢复性和隐藏数据访问模式展开研究,提出了证明数据的可持有性,实现数据的可恢复性,并且隐藏了数据的访问模式。
2 相关研究
Juels和Kaliski[3]最先提出了可恢复性证明(proof of retrievability,POR),并提出基于哨兵的方案。其基本思想是先对原文件F加密,再用纠错码对加密后的文件F’进行编码形成文件F”,然后在F”中随机选取若干哨兵,每一个哨兵可监测一部分数据,并将这些哨兵的值存储在客户端,然后把文件F”存储在云端。客户可以利用哨兵质询服务器,验证文件的可恢复性。与此同时,Ateniese等人[4]提出了可证明数据拥有 (provable data possession,PDP)模型,并提供了基于RSA模指运算构造同态标签以实现数据持有性证明。这两种模型的主要区别是PDP只验证了数据是否完整,而没有考虑遭到破坏后的数据是否可恢复。在他们研究的基础上,又有很多研究者提出了一些改进方法和新的方案[5~9]。其中,陈兰香[9]提出一种基于同态散列的数据持有性证明方法,利用同态散列算法的同态性,即两数据块之和的散列值与它们散列值的乘积相等,验证数据的持有性。但这两种模型有一个共同缺点,它们只考虑了数据的持有性或可恢复性,没有对客户访问数据模式进行隐藏,使得敌手可以跟踪客户对数据访问的模式,从中获取信息。另外,在POR模型中,如果数据所在的磁盘存储块受到物理损伤,或敌手大量篡改数据,即使使用纠错码也无法恢复原有数据。
Goldreich最早提出 ORAM (oblivious random access machine),并与Ostrovsky[10]提出了隐藏客户对存储器的访问模式以防止软件逆向工程。随着云计算的发展,ORAM在云存储隐私保护方面也有着重要的应用[11]。在参考文献[10]中提出的最有效的算法是金字塔形分层算法,它对数据所占用的存储块按金字塔形状管理,该算法分为访问和洗牌两个阶段。访问阶段又分为读和写两部分,在读部分,ORAM顺序读取金字塔形第1层所有盒子中的数据块,然后再读其他每一层中的某一个盒子(由散列函数决定)中的数据块。在整个读过程中,如果找到了目标数据块,则后继选择哑元块读取。写部分比较简单,对目标块进行处理后写入第1层中的空位置即可。但由于客户的每一次请求都会将数据块写入第1层,当第1层放满数据块后需要将第1层和第2层的数据块重新排列后存放到第2层中,第1层清空。类似地,在第2i次数据访问之后,第i层的数据块和第i+1层的数据块重新排列后存储到第i+1层,前i层清空,这个过程称作洗牌。洗牌是分层算法中最复杂的阶段,它是该算法性能的瓶颈。洗牌的关键操作是无关地排序数据块。若采用AKS网络排序算法时,平均时间复杂度为O(clog3N),若采用巴切排序算法时,平均时间复杂度为O(dlog4N)(c>>d)。在洗牌阶段若客户访问数据,客户可能会等待较长时间。因此,这样的算法若应用于实际环境中则无法让人容忍它的低效率。许多研究者[11~16]在分层算法的基础上又提出了一些新的算法,旨在降低存储空间占有量和平均访问时间复杂度。但这些算法均由访问和洗牌两个阶段构成,洗牌仍是算法的瓶颈。
本文提出一种ORAM结构,在需要少量客户端存储空间和线性级服务器存储容量的情况下,把洗牌过程均摊到每次访问操作中,使得对服务器的访问时间可保持在常量级。同时结合同态散列算法验证数据的可持有性并利用副本实现数据的可恢复性。
3 ORAM结构
ORAM模型机可以隐藏客户对服务器的访问模式,即除客户外,其他任何角色每次看到客户对数据的访问序列都是相似的。本文假定ORAM模型机是由可信任的客户端和不可信的服务器端构成。
3.1 服务器中文件的结构
假设客户文件是由N个数据块组成,每个数据块在服务器端存储两份,并增加2N个哑元块使得敌手观察客户的访问模式时无法确认哪个是真实的数据块。在本方案中总共需要4N个服务器存储块,利用随机均匀函数将2N个数据块映射到4N个存储块中,剩余存储块存放哑元块。
为了提高数据存储的可靠性,可将一个大数据文件分割成若干大小为S个存储块的文件存储。由于客户的一个数据块在服务器中有两个备份,且随机均匀地分布在不同的文件中,当一个文件损坏时,该文件中的所有数据块均可从其他的文件中恢复。
3.2 客户端数据结构
在客户端设置BufM和BufA两个缓冲器,两张数据表SerMap[4N]和 PosMap[N]。
BufM是一个可存放6个存储块的缓冲器。采用FIFO算法对BufM进行管理,将每次客户所访问的数据块存放到该缓冲器中。
BufA的大小与BufM相等,每次读/写数据块时,将随机读的数据块和哑元块存放到该缓冲器中;当客户是写操作时,会把一个备份放到该缓冲器中;当BufM满时会将其中一个最久未用的数据块移到BufA中,以保证每次客户在访问云存储时,BufM至少有一个空闲块。如果BufA不满则用哑元块填满。最后将BufA中的数据块写回云存储器中。
数据表SerMap描述存储在服务器上各数据块的属性,每次访问服务器时均需要调整该表内容,以适应ORAM的变化。该表有6个域,分别是FlagD、FlagA、Fresh、PdpG[8]、PdpA[8]和 PdpH[8]。FlagD 为数据块标识,其值为1表示该块为数据块,否则为哑元块。FlagA标识存储块最近是否被访问过。每当一个存储块读到缓冲器中时,设置该块对应的FlagD为0;FlagA为1,表示该存储块为哑元块且最近被访问过。当一个数据块被写入服务器时,会随机找一个最近没被访问过的哑元块写入,并修改该块对应的FlagD为1。在查找哑元块的过程中,若其对应的FlagA为1,则修改其值为0,以便下次查找到该块时能被选中。Fresh表示服务器存储块的新鲜度,初值为随机数,用于数据的加解密,在对存储块的每次读操作后其值加 1;PdpG[8]、PdpA[8]和 PdpH[8]与验证 数据的持有性有关,参见第3节。
数据表PosMap表示用户数据块在服务器中存放的位置映射,每次读写数据块时均需对该表进行修改。该表有3个域,分别是SaveF、Addr1和Addr2。Addr1和Addr2分别表示一个数据块在服务器中的两个备份位置,也是数据表SerMap的索引。SaveF表示数据块存放在服务器/本地的标识,当其值为0时,表示数据块的两个备份都在服务器中存放;当其值为1或2时,表示数据块在BufM中,且一个备份在服务器上 (SaveF=1时,Addr2有效,SaveF=2时,Addr1有效);当其值为3时,表示数据块同时在BufM和BufA中,且服务器中的备份失效。
4 数据可持有性证明
4.1 同态散列算法
本文借鉴参考文献[9]选择同态散列算法验证数据的持有性。假设在存储块大小为128 KB的空间中随机选取8个片段,每个片段4 KB。用1 024×8矩阵表示8个片段则为:

其中 bi=(bi,0,bi,1,…,bi,1023)(0≤i≤7)表示片段,bi,j∈Zp(0≤i≤7,0≤j≤1 023),Zp是以足够大的正素数 p 为模的有限域,两个片段相加规则定义为:

同态散列计算过程如下。
(1)计算每个片段的散列值

其中,g=(g0,g1,…,g7)是 1×8 的向量,gi∈Zp(0≤i≤7)。
(2)所有片段的散列值构成一个1×8的向量h

(3)散列同态性质
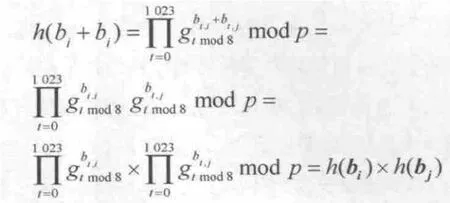
4.2 数据持有性证明
在存储数据块时,先对数据块进行加密处理后,随机产生向量g,在数据块中任意选择8个位置a(数据片段的起始位置),并计算各片段的散列值h。最后将g、a和h分别保存到 SerMap表中的 PdpG[8]、PdpA[8]和 PdpH[8]数组中。
可以选择3种方法对数据进行持有性证明:客户自己审计;服务器审计;第三方审计。以服务器审计为例介绍审计步骤。
算法1 审计算法 Boolean Audit(M)
输入:M,对服务器中M个数据块进行验证
输出:布尔值,若为真则表示审计通过,否则失败
Boolean Audit(M)
(1)for(i=0;i (2)u=RandBlock();//随机选择一个存储块号 (3) Addr1=SerMap[u].PdpA[Rand()];//在 SerMap[u]表项中随机选择一个片段的起止 (4) Addr2=SerMap[u].PdpA[Rand()];//在 SerMap[u]表项中随机选择另一个片段的起止 (5) value=Challenge(u/S,u%S,//对云存储文件[u/S]中的第u%S块进行质询 SerMap[u].PdpG,Addr1,Addr2);//向量 g和两个片段地址 (6) if (value!=SerMap[u].PdpH.Addr1*SerMap[u].PdpH.Addr2){//判断验证是否失败 (7) Alert(u,“Bad”);//失败时,发出警报 (8) return false;} (9)} (10)return true//验证成功,返回 算法1随机选择M个存储块进行验证,由质询函数Challenge()向服务器提出质询,服务器根据提供的参数计算两个片段之和的散列值,并返回该值。如果该值与本地储存的两个片段的散列值之乘积相等则说明数据是完整的,验证成功。否则,说明数据块已遭到破坏,需要报警处理并从另一个备份中恢复数据。 每次审计均随机选择M个数据块进行验证,而N远大于M,所以,每次审计时选择相同序列的数据块的概率极小,并且,在验证某一个数据块时仅向服务器提供向量a中的任意两个地址,服务器无法一次获取a中的所有地址。另外,在ORAM模型中,所访问过的存储块将会动态地迁移到新的位置,需要重新计算该块的向量g和a,因此,服务器很难伪造各存储块的审计结果,系统安全性可以得到保障。 客户读/写数据块只需执行LookUp()即可,通过LookUp()可以隐藏数据的访问模式。 算法 2 void LookUp(op,u,data) 输入:op,表示客户对服务器的访问操作,read/write u,表示客户需要访问的数据块 data,客户数据存储地址 输出:无 void LookUp(op,u,data) (1)RandRead(data);//随机从服务器读一个数据块,并存放到BufA中 (2)RandRead(DUMMY);//随机读一个哑元块,并存放到BufA中 (3)if(ExistBuf(u)){//如果 u 已在 BufM/BufA 中 (4)RandRead (DUMMY);//则随机读一个哑元块,并存放到BufA中 (5)RemoveBuf(u);//将u从 BufA/BufM 移出 (6)}else Read(u);//否则读指定的数据块u (7)if(op==write){//如果是写操作 (8)copy(data,u);//将数据复制到u中,修改 PosMap中第u表项中的 SaveF为 3;//并将 Addr1、Addr2所指SerMap对应项中的FlagD设置为0。 (9)copy(data,BufA);将 data 复制到 BufA 中的一个缓冲区中,以备写入云存储中 (10)}else copy(u,data); (11)EnterBufM(u);//将 u插入 BufM 的队尾 (12)RandRead(DATA);//随机从服务器读取一个客户数据块,并存放到BufA中 (13)RandRead (DUMMY);//随机读一个哑元块,并存放到BufA中 (14)Update();//将数据块和哑元块写入服务器 (15)return 在该算法中步骤(1)和步骤(11)任意读两个客户数据块,步骤(2)和步骤(12)任意读两个哑元块。当所需要访问的数据块不在BufM或BufA中时,则读取并放到BufM的队尾,否则随机读一个哑元块,并将数据块从BufM或BufA中移出再插入BufM的队尾。 当op是写操作时,则将内容写入u缓冲区中 (步骤(8)),并将一个备份存放到 BufA(步骤(9))中。步骤(14)将BufA中的存储块写回服务器,实现数据的更新。 RandRead()可随机读取一个数据块/哑元块,Read(u)读取指定的数据块u,在读数据块或哑元块后,需要调整两张数据表PosMap和SerMap的相关内容,并且,每读一个存储块,都可以选择使用验证数据的可持有性。 在Update算法中,当BufM已满时,则将最久未用的数据块移入BufA中,以保证在每次执行LookUp操作之前,BufM中最少有一个缓冲区是空的。在执行LookUp操作时,最多有6个数据块/哑元块进入BufA中,可能是3个数据块和3个哑元块的组合,也可能是4个数据块和2个哑元块的组合;最多有1个数据块进入BufM中。Update只将BufA中的内容写入服务器。Update算法描述如下。 算法3 淘汰数据块算法void Update(void) void Update(void) (1)if(BufM满)将最久未用缓冲区数据移到BufA中; (2)if(BufA 未满)以哑元块填满; (3)for(i=0;i<6;i++)给 BufA 中的每一个缓冲区随机分配一个标签; (4)对BufA中的缓冲区按标签值大小排序,形成一个新的缓冲序列; (5)for(i=0;i<6;i++){//为 BufA 中的 6个数据块/哑元块寻找存储位置 (6)在SerMap中随机找一个最近未被访问过的哑元块x,即FlagA值为0的哑元块,若FlagA值为1时,将其值设置为0,继续随机查找下一个哑元块; (7)if(BufA[i]是数据块) 设BufA[i]对应的数据块号为u,访问PosMap中第u表项,若SaveF的值为 1或2,则用有效项Addr2或Addr1减去x,若其值的绝对值小于S,则转到步骤(6)重新选择哑元块x,此步可保证客户数据块的两个备份存放在不同的文件中;否则,若 SaveF的值为 3,则修改 Addr1或 Addr2为x,且修改SaveF为1或2;否则,修改Addr1或Addr2为x,且修改SaveF为0; (8)加密,产生向量g及随机选取片段地址a,计算其散列值,然后将数据块写入文件[x/S]的第[x%S]块中,修改SerMap中第x表项中的FlagD为1,FlagA为1,将向量g、片段的起止地址a及其散列值存入相应位置;} (9)return 假定一个存储块大小为128 KB,需要服务器的存储容量是实际数据量的4倍,当数据文件很大时,客户端数据结构所需容量是服务器存储容量的0.07%左右。客户每访问一个数据块,均需要读/写11块服务器的存储块,其中读5次写6次。 安全定义[11]:设 y=((op1,u1,data1),(op2,u2,data2),…,(opM,uM,dataM))是客户请求访问某一数据块时ORAM访问服务器存储块的一个序列,其长度为M。其中op表示R(读)或W(写)操作,u表示服务器虚拟存储地址,data表示客户存储器地址,当op为read操作时,data指从服务器读取的数据存放在客户端的地址,当op为write操作时,data指写往服务器的数据在客户端存放的地址。用A(y)=(op1,op2,…,opM)表示客户访问服务器的操作序列。如果对于任何两个客户访问序列y和y’,只要其长度相等,访问服务器的操作序列一样,对任何人(除客户本人)来说 A(y)和 A(y’)都是在计算上不可区分的,则称该ORAM结构是安全的。 本文客户访问服务器的操作序列是A(y11)=(R1,R2,R3,R4,R5,W6,W7,W8,W9,W10,W11),客户不论是读还是写数据块,其访问服务器的操作均为A(y11),因此,本文所提ORAM结构是安全的。 在LookUp算法中,数据块u在服务器上的存储位置是随机分布的,读取u和4次随机读服务器存储操作混在一起,敌手很难辨认哪一块是客户需要的,并且敌手很难知道下一次它将存放在哪一个位置。在访问服务器的过程中不会出现刚被存储到服务器上的数据块又要被访问的现象。因为,每个数据块都有两个备份,如果在访问中发现所访问的数据块是刚刚写入服务器的数据块,则可以通过访问该数据块的另一个备份来获取数据块。因此,敌手无法从访问服务器的序列中获取有用的信息,系统是安全的。 本文提出的常量级访问模式仅需占用线性级服务器存储容量,实现无关访问服务器。将大的文件分割成小文件存放,每个数据块都有两个备份,且存放在不同的文件中,使得数据的可恢复性得到保障。利用同态散列算法实现数据可持有性证明。但该方法需要占用客户端存储空间,当数据文件超大时,所需客户存储空间也随着增大,因此,需要进一步探索减少客户端存储空间的使用量。 1 Wang C,Ren K,Lou W J,et al.Toward publicly auditable secure cloud data storage services.IEEE Network,2010,24( 4):19~24 2 李红卫,古春生,白凤娥.安全访问外包数据的研究.电子技术应用,2013,39(7):54~56 3 Uels A,Kaliski B S.Pors:proofs of retrievability for large files.Proceedings of the 14th ACM Conference on Computer and Communications Security,Alexandria,USA,2007:584~597 4 Ateniese G,Burns R,Curtmolar R,etal.Provable data possession at untrusted stores.Proceedings of the 14th ACM Conference on Computer and Communications Security,Alexandria,USA,2007:598~609 5 Shacham H,Waters B.Compact Proofs of Retrievability.Proceedings of Asiacrypt’08,Melbourne,Australia,2008 6 Dodis Y,Vadhan S P,Wichs D.Proofs of retrievability via hardness amplitication.Proceedings of the 6th Theory of Cryptography Conference,San Francisco,2009:109~127 7 朱岩,王怀习,胡泽行等.数据可恢复性的零知识证明.中国科学:信息科学,2011,41(10):1227~1237 8 梁彪,曹宇佶,秦中元等.云计算下的数据存储安全可证明性综述.计算机应用研究,2012,29(7):2416~2421 9 陈兰香.一种基于同态Hash的数据持有性证明方法.电子与信息学报,2011,33(9):2199~2204 10 Goldreich O,Ostrovsky R.Software protection and simulation on oblivious RAMs.Journal of the ACM,1996,43(3):431~473 11 Elaine S T H,Chan H,Stefanov E,et al.Oblivious RAM with O((logn)3) worst-case cost.Proceedings of the 17th International Conference on the Theory and Application of Cryptology and Information Security,Seoul,South Korea,2011 12 Pinkas B,Reinman T.Oblivious ram revisited.Proceedings of CRYPTO,California,USA,2010 13 Goldreich O.Towards a theory of software protection and simulation by oblivious RAMs.Proceedings of STOC 1987,New York,1987 14 Damgard I,Meldgaard S,Nielsen J B.Perfectly secure oblivious RAM without random oracles.Proceedings of TCC 2011,Rhode Island,USA,2011 15 Goodrich M T,Mitzenmacher M.Privacy-preserving access of outsourced data via oblivious ram simulation. Automata,Languages and Programming,2011(5) 16 Kushilevitz E,Lu S,Ostrovsky R.On the(in) security of hash-based oblivious ram and a new balancing scheme.Proceedings of SODA,Kyoto Japan,20125 访问模式
5.1 LookUp算法
5.2 Update算法
5.3 性能与安全分析
6 结束语
