空间谱估计经典算法性能比较

石国德，王明皓，吕朝晖

（1.沈阳航空航天大学 辽宁 沈阳 110136；2.沈阳飞机设计研究所 辽宁 沈阳 110035）

空间谱是阵列信号处理中的一个重要概念，“空间谱”表示信号在空间各个方向上的能量分布。若能够估计出空间谱就可以得到信号源的波达方向 （direction of arrival，DOA），所以空间谱估计也常称为DOA估计。

最早的阵列的DOA估计算法可以追述到常规波束形成算法（CBF）法[1]，也叫做Bartlett波束形成算法，该算法是时域傅里叶谱估计在空域的一种简单扩展，即用空域各阵列数据代替传统时域处理的时域数据，与时域傅里叶变换一样空域分辨力受到空域傅里叶限即瑞利限的限制。故CBF不能分辨一个波束宽度内的多个信号源。接着突破瑞利限的DOA估计算法如非线性估计算法如Capon波束形成技术[2]得到了研究。

20世纪70年代起利用子空间分解类的算法开始兴起，最具代表性的经典算法有：1）多重信号分类（MUSIC）[3]，即利用接收数据的协方差矩阵进行特征分解得到两个相互正交的信号子空间和噪声子空间，信号的子空间的划分依据是与阵列流形空间构成相同的空间，剩余构成噪声子空间。利用噪声子空间与阵列流形正交构造出空间谱（并不代表能量分布，只说明噪声子空间和阵列流形的正交程度），从而得到DOA估计。2）旋转不变信号子空间算法（ESPRIT）[4-5]，是以阵列流形中隐含的空间平移不变性，即阵列形式可以划分成两个完全相同的子阵，从而利用与阵列形成相同空间的信号子空间得到旋转不变方程，然后利用各种解旋转不变方程方法如最小二乘 （LS）[4]、总体最小二乘（TLS）[5]解方程得到DOA估计。

20世纪80年代后期又出现了一批子空间拟合类算法，比较经典的有最大似然（ML）[6]算法、子空间拟合（SF）[7]算法，但由于DOA估计似然函数是非线性的，故求其最优解需要多维搜索，运算量比较大。

1 DOA估计经典算法

1.1 DOA估计信号模型

考虑p个远场窄带信号入射到空间M阵元的均匀线阵（ULA），这里假设阵元数等于通道数，即各阵元接收到信号后经各自的传输通道送入到处理器，还假设目标为点目标，第一个阵元为参考点，为避免测角模糊设阵元间距为半波长。则信号模型用矢量形式可表示为：

其中 X（t）表示 M×1 维接收快拍数据矢量，S（t）为 P×1 维信号源矢量，N（t）为M×1维噪声数据矢量，为了方便分析这里假设噪声为均值为0、方差为σ2的高斯白噪声。A表示空间 M×N 的阵列流形矩阵，A=[a（θ1）,a（θ2），…，a（θP）]，其中第p（p=1，…，P）个信号阵列流形为 a（θp）=[1，exp（jπsinθp），…，exp（jπ（M-1）sinθp）]。 DOA 估计技术可理解为从模型（1）中估计出P个未知参量θp（p=1，…，P）。下面介绍6种经典算法。

1.2 常规波束形成（CBF）

假设 M 个阵元的加权矢量为 w=[w1，w2，…，wM]T，则整个阵列的输出为y=wHx（t），那么L次快拍输出的平均功率为

其中R为接收阵列的协方差矩阵。当加权值为w=a（θ）时，式（2）即为CBF空间谱图，等于

通过扫描得到得到谱曲线，找到P个谱峰所对应的角度值就得到了DOA估计值。

1.3 Capon波束形成

可以证明式 （2）的波束形成的最优权矢量为wopt=则整个阵列的输出可以简化为

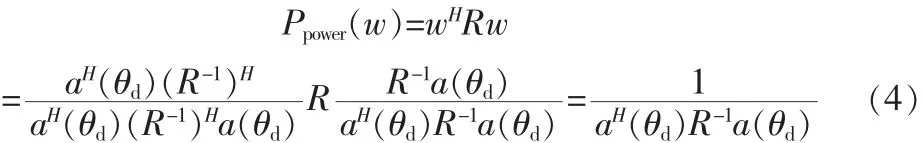
由于期待信号是未知的，可通过扫描得到Capon波束形成谱曲线即

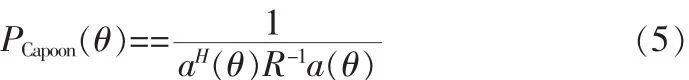
亦叫做最小方差法（MVM），找到个谱峰所对应的角度值就得到了DOA估计值。

1.4 多重信号分类（MUSIC）

MUSIC算法的提出开创了信号谱估计算法研究的新时代，促进了特征结构类算法的兴起和发展，该算法以成为空间谱估计的标志性算法。该算法不同于上述两种算法，上述算法是针对接收数据协方差矩阵进行直接处理。而MUSIC算法需要对协方差矩阵进行特征值分解，即

US是由P个大特征值对应的特征矢量张成的信号子空间，UN是由M-P个小特征值对应的特征矢量张成的子空间也即噪声子空间。需要指出的是这里的P值是未知的，需要用信息论方法或者平滑秩方法等事先估计。信号子空间和噪声子空间是正交的，故理想条件下阵列流形正交于噪声子空间，即aH（θ）UN=0。但是实际接收阵列协方差矩阵是有偏差的，可用有限个快拍数据来估计即行特征值分解得到近似噪声子空间但该噪声子空间并不与阵列流形完全正交。因此可以通过下面的空域搜索得到MUSIC空间谱：

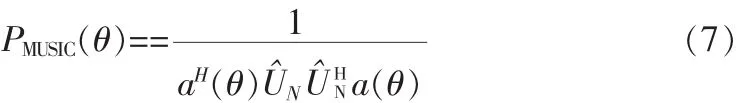
1.5 旋转不变子空间算法（ESPRIT）

ESPRIT算法最基本的假设是存在2个完全相同的子阵，且两个子阵间的间距是Δ已知的。假设两个相同的子阵分别为：

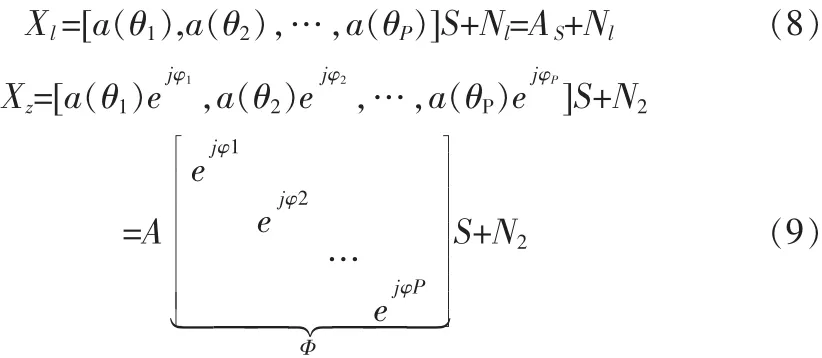
其中 φp=（2πΔsinθp/λ），由上述可知只要得到两个子阵间的旋转不变关系Φ就可求取DOA估计值。将两个子阵模型合并得：

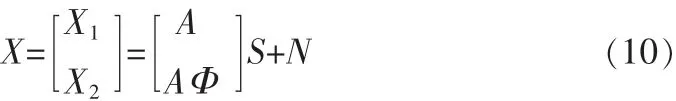
类似于MUSIC算法，对上述接收协方差矩阵进行特征分解得到信号子空间

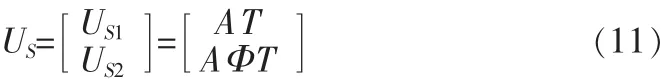
则可得到

对式（12）进行解方程可得Ψ=U*S1US2（LS结果），上标*表示pense-moore伪逆。再对Ψ进行特征分解得到Φ，进而可求取DOA估计值。

1.6 最大似然估计（ML）

在对最大似然进行推导之前先限定几点：1）信号协方差矩阵是正定的；2）阵元数大于信号源数，快拍数大于阵元数；3）不同快拍之间的噪声是不相关的，且为服从正态分布的加性白噪声。对于确定性对大似然即是假设信号源是确定未知的最大似然。L次快拍服从的联合条件概率密度函数：

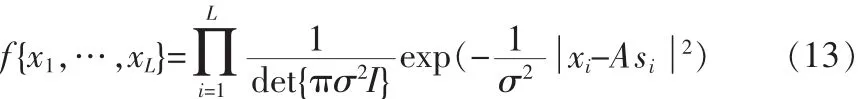
det{·}表示矩阵的行列式。对式（13）两边取负对数得到：

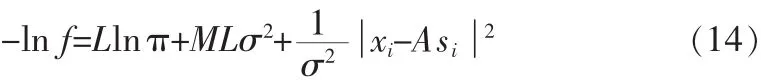
对于式（14）未知σ2，s并不是我们所关心的，故固定其余两个未知量给出一个量的最大似然估计：=tr{P}，=A*x，其中 PA=A（AHA）-1AH表示矩阵 A 的投影矩阵，A*表示矩阵A的伪逆。把这两个似然估计值代入式（14）并忽略常数项可得到θ的最大似然估计为：

1.7 子空间拟合（SF）

子空间拟合与最大似然类似，最大似然是接收数据与真实数据的拟合，而子空间拟合是信号子空间或噪声子空间于真实的子空间的拟合。为了简要说明这里只给出信号子空间拟合（SSF）。快拍数无限情况下有US=AT，但事实上快拍数有限情况下只是近似，可通过构造一个拟合关系来找出T使得两者在最小二乘意义下拟合的最好，定义如下拟合关系：

T^作为辅助参量可以用最小二乘求解得：

将式（17）代入到式（16）得到SSF的求解的代价函数：

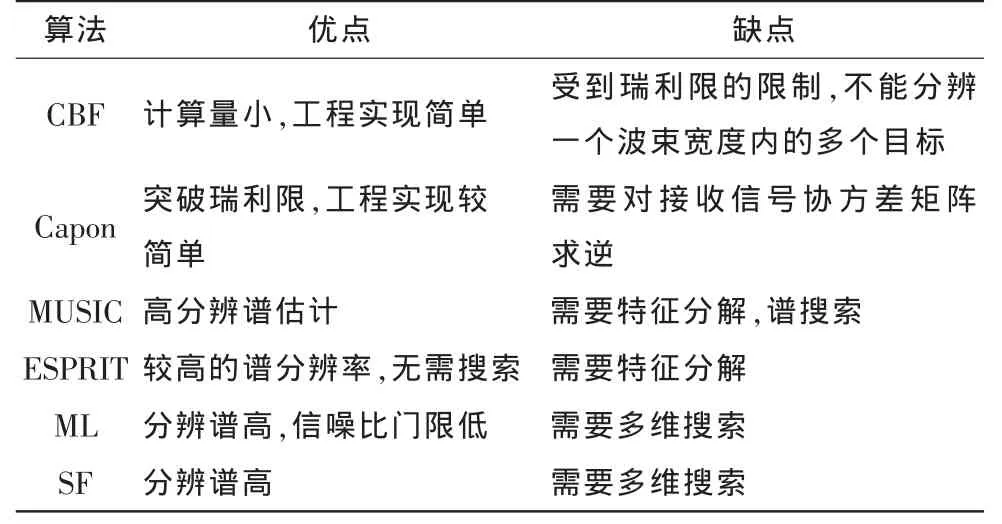
表1 各算法优缺点综述Tab.1 Each algorithm and disadvantages summary

2 仿真比较与性能分析

2.1 单信号DOA估计性能随信噪比变化曲线

考虑ULA的阵元数M=10，快拍数L=100，单个目标信号源DOA参数为θ=30°，图1给出均方根误差RMSE比较图，RMSE定义如下

其中，k表示蒙特卡洛实验次数，θ^，θ分别为信号源DOA估计值和真值。由图1可以看出单信号源情况下，ML和CBF方法的均方根误差最小，其次是MUSIC和SSF，接着为Capon，最差的是ESPRIT。但是文中的6种方法信噪比门限基本一致。

2.2 单信号DOA估计性能随快拍数变化曲线

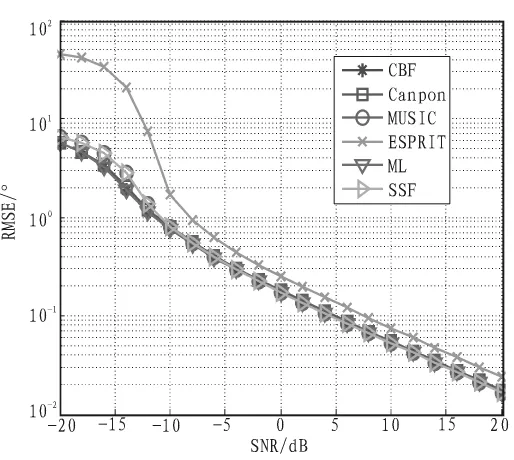
图1 DOA估计性能随信噪比变化曲线Fig.1 Estimation performance with SNR change curve

该仿真信噪比SNR=10 dB，快拍数变化，其余仿真条件与2.1相同，图2给出单信号情况下DOA估计性能随快拍数变化曲线。从图2可以得到与2.1相同的结论，但需要注意的是在快拍数较小的时候（此处为10个快拍），Capon波束形成算法的性能是最差的。

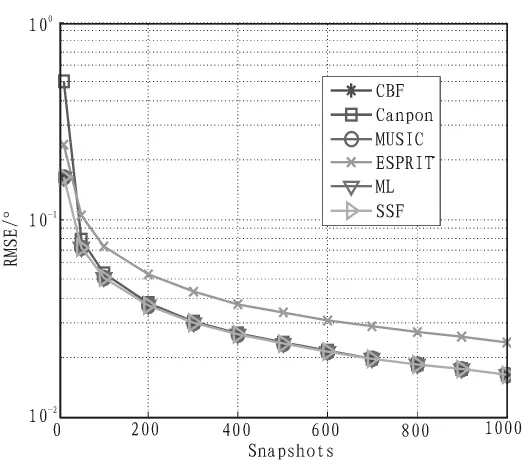
图2 DOA估计性能随快拍数变化曲线Fig.2 Estimation performance with number of snapshots change curve

2.3 单信号DOA估计性能随阵元数变化曲线

该仿真信噪比SNB=10 dB，其余仿真条件与2.1相同，图3给出单信号情况下DOA估计性能随阵元数变化曲线。从图3得到与2.1相同的结论。

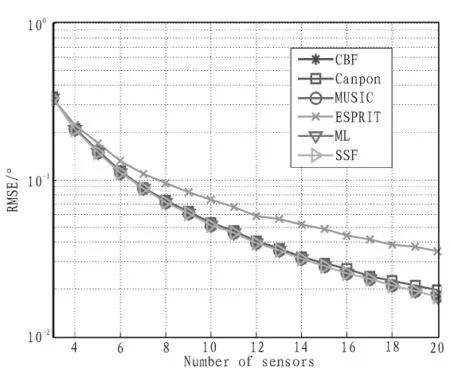
图3 DOA估计性能随阵元数变化曲线Fig.3 Estimation performance with number of array elements change curve

2.4 双信号DOA估计性能随信噪比变化曲线

考虑ULA的阵元数M=10，快拍数L=100，两个目标信号源 DOA 参数为 θ=[30°，35°]， 图 4给出信号比为 SNR=10 dB的空间谱图，从图4（a）中可以看出MUSIC算法分辨率高于Capon波束形成，而Capon波束形成高于CBF。

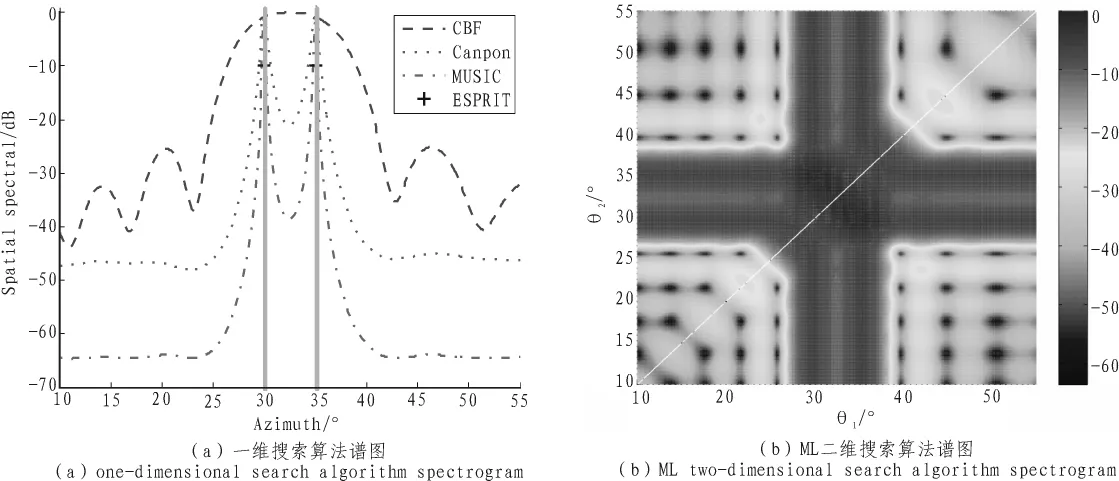
图4 搜索算法谱图Fig.4 Search algorithm spectrogram classification

3 结 论

文中对近几十年的空间谱估计经典算法进行了总结，对比了各种经典算法的性能，列出了各种算法的优缺点，使得工程操作员在DOA估计算法实现时提供了理论依据，总结如下：1）若芯片处理速度不够快，要求精度不高时，可选择CBF和ESPRIT算法，这3种算法计算量相对来说不是很大，实时性较容易实现。2）芯片处理速度相对较快，要求精度较高时，可选择Capon和MUSIC算法。3）芯片处理速度快，要求精度高时，可选择ML和SF算法。

[1]Krim H，Viberg M.Two decades of array signal processing research[J].IEEE Singal Processing Magazine，1996，13（4）:67－94.

[2]Capon J.High-resolution entropy spectral analysis[J].Proceedings of IEEE，1969，57（8）:1408－1418.

[3]Schmidt R.Multiple emitter location and signal parameter estimation [J].IEEE Transactions on Antennas and Propagation，1986，34（3）:276－280.

[4]Roy R，Kailath T.ESPRIT-a subspace rotation approach to estimation of parameters of cissoids in noise [J].IEEE Transactions on Acoustics Speech and Signal Processing 1986，34（10）:1340－1342.

[5]Roy R，Kailath T.ESPRIT-estimation of signal parameters via rotational invariance techniques [J].IEEE Transactions on Acoustics Speech and Signal Processing，1989，37 （7）:984－995.

[6]Stoica P，Nehorai A.MUSIC，maximum likelihood，and cramerrao bound[J].IEEE Transactions on Acoustics Speech and Signal Processing，1989，37（5）:720－741.

[7]Viberg M，Ottersten B，Kailath T.Detection and estimation in sensor arrays using weighted subspace fitting[J].IEEE Transactions on Acoustics Speech and Signal Processing 1991，39（11）:2436－2449.