带有不可用区间的单机排序问题

刘 澈，罗成新

（沈阳师范大学数学与系统科学学院，沈阳 110034）

带有不可用区间的单机排序问题

刘 澈，罗成新

（沈阳师范大学数学与系统科学学院，沈阳 110034）

考虑的是带有到达时间、拒绝工件、不可用区间的单机排序问题。一个工件或者被拒绝加工，或者被接受。若工件被拒绝加工，厂家必须支付一定的拒绝惩罚；若工件被接受，则把工件放在机器上进行加工。在张丽琦工作的基础上增加了一个不可用区间，机器在此区间内不能加工工件，并且在同一时刻至多加工一个工件。目标函数是最小化所有接受工件的时间表长与所有拒绝工件的拒绝惩罚之和。首先给出一个动态规划算法，然后通过构造输入，将拒绝惩罚进行取整运算，再通过动态规划算法，得到拒绝惩罚取整后的一个最优排序，按照这个工件排序得到原问题的一个可行排序，最后借助一个3—因子算法得到一个全多项式时间近似方案。

到达时间；拒绝工件；不可用区间；时间表长

在经典排序问题中，所有的工件必须被接受，拒绝工件是不允许的。然而，在实际生产中，厂家为了获得更大的利润，通常会拒绝那些加工时间长且获利相对小的工件，也因此得到一定的惩罚。在加工工件时，通常也会因为机器故障、工人问题等其他原因造成机器在某一时间段内不能加工工件，即产生了不可用区间。由于上述问题的实用性，带有拒绝工件及不可用区间的排序问题得到了越来越多人的关注。

Zhang等［1］研究的是带有到达时间和拒绝工件的单机排序问题，证明出文献所研究的问题是NP－难的。此外，还有许多文献研究的也是带有拒绝工件的排序问题［2－4］。Kacem［5］研究的是在带不可用区间的条件下，极小化时间表长问题。Kacem等［6］研究的是带不可用区间的极小化加权流时间的单机排序问题。此外，文献［7-10］研究的也是带有不可用区间的排序问题。Woeginger［11］研究的是满足一定条件的动态规划算法能够得到全多项式时间近似方案，文献［12-14］是对相应的问题分别得到了全多项式时间近似方案。

本章在文献［1］的基础上加了一个不可用区间，运用文献［1］的方法设计了一个全多项式近似方案。

1 问题描述

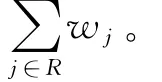
2 动态规划算法

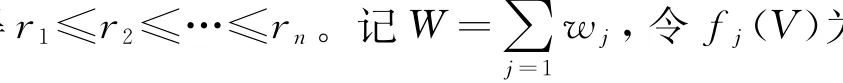
3 全多项式近似方案Aε

算法Aε

4 结 论

本章考虑的是带有到达时间，拒绝工件，不可用区间的单机排序问题，目标函数是最小化时间表长与所有拒绝工件的惩罚的和。给出了一个动态规划算法及一个全多项式时间近似方案，此全多项式时间近似方案的时间复杂性为

［1］ZHANG Liqi，LU Lingfa，YUAN Jinjiang.Single machine scheduling with release dates and rejection［J］.Eur J Oper Res，2009，198（3）：975-978.

［2］LI Shisheng，YUAN Jinjiang.Parallel-machine scheduling with deteriorating jobs and rejection［J］.Theor Comput Sci，2009，411（40／41／42）：3642-3650.

［3］CHENG Yushao，SUN Shijie.Scheduling linear deteriorating jobs with rejection on a single machine［J］.Eur J Oper Res，2009，194（1）：18-27.

［4］SEIDEN S S.Preemptive multiprocessor scheduling with rejection［J］.Theor Comput Sci，2001，262（1／2）：437-458.

［5］KACEM I.Approximation algorithms for the makespan minimization with positive tails on a single machine with a fixed non－availability interval［J］.J Comb Opt，2009，17（2）：117-133.

［6］KACEM I，MAHJOUB A R.Fully polynomial time approximation scheme for the weighted flow-time minimization on a single machine with a fixed non-availability interval［J］.Comput Indust Eng，2009，56（4）：1708-1712.

［7］KACEM I.Approximation algorithms for the makespan minimization with positive tails on a single machine with a fixed non-availability interval［J］.J Comb Optim，2009，17（2）：117-133.

［8］MOSHEIOV G，ORON D.Due-date assignment and maintenance activity scheduling problem［J］.Math Comput Modeling，2006，44（11／12）：1053-1057.

［9］KELLERER H，KUBZIN M A，STRUSEVICH V A.Two simple constant ratio approximation algorithms for minimizing the total weighted completion time on a single machine with a fixed non-availability interval［J］.Eur J Oper Res，2009，199（1）：111-116.

［10］MOSHEIOV G，SARIG A.Scheduling a maintenance activity to minimize total weighted completion-time［J］.App Math Comput，2009，57（4）：619-623.

［11］WOEGINGER G J.When does a dynamic programming formulation guarantee the existence of a fully polynomial time approximationscheme（FPTAS）？［J］.Informs J Comput，2000，12（1）：57-75.

［12］KACEM I.Fully polynomial time approximation scheme for the total weighted tardiness minimization with a common due date［J］.Discrete Appl Math，2010，158（9）：1035-1040.

［13］KELLERER H，STRUSEVICH V A.A fully polynomial approximation scheme for the single machine weighted total tardiness problem with a common due date［J］.Theor Comput Sci，2006，369（1／2／3）：230-238.

［14］乔玉，罗成新.具有禁用区间的平行机排序时间表长问题的全多项式近似方案［J］.沈阳师范大学学报：自然科学版，2012，30（1）：12-15.

［15］刘澈.带到达时间和不可用区间以及拒绝工件的排序问题［D］.沈阳：沈阳师范大学，2013.

Single machine scheduling problem with unavailable interval

LIU Che，LUO Chengxin

（School of Mathematics and System Science，Shenyang Normal University，Shenyang 110034，China）

In this paper，we consider a single machine scheduling problem with release dates，rejection and an unavailable interval.A job is either rejected，in which case a rejection penalty has to be paid，or accepted and processed on the machine.Based on the work of Zhang Liqi，we add an unavailable interval，in that the machine is unavailable in an unavailable interval，and it can process at most one job at a time.The objective is to minimize the sum of the makespan of the accepted jobs and total rejection penalty of the rejected jobs.First we propose a dynamic programming algorithm，and construct the input，then round the input and get an optimal schedule by the dynamic programming algorithm，and thus get a feasible schedule for the original problem.Finally we obtain a fully polynomial-time approximation scheme for this problem by using 3-approximation algorithm.

release dates；rejection；unavailable interval；makespan

O223

A

10.3969／j.issn.1673-5862.2013.03.009

1673-5862（2013）03-0353-03

2012-09-18。

国家自然科学基金资助项目（61070242）。

刘 澈（1988-），女（满族），辽宁鞍山人，沈阳师范大学硕士研究生；罗成新（1958-），男，辽宁新宾人，沈阳师范大学教授，博士，硕士研究生导师。