概率论与数理统计案例教学方法探析

王 昕，程希明

（北京信息科技大学理学院，北京 100192）

概率论与数理统计案例教学方法探析

王 昕，程希明

（北京信息科技大学理学院，北京 100192）

概率论与数理统计不仅是数学专业的必修课，也是经管类和工科类专业的基础课，其覆盖面广，应用性强，是一门理论与实践密切结合的课程。以案例驱动教学法作为概率论与数理统计课程教学方法改革的一种手段，有针对性的选取了条件概率、全概率公式、数学期望、大数定律等4个重要的知识点，并使用贴近实际生活的案例作为教学的切入点，详细分析解决实际问题的过程，向学生介绍该课程的相关知识在现实中的广泛应用，引导学生从实际情境中发现问题。课堂教学实践证明，基于案例驱动的教学方法能够开阔学生的视野，对于课程建设、教学效果、教师及学生能力的提高都有重要意义。

案例驱动；全概率；数学期望；大数定律；置信区间

0 引 言

概率论与数理统计是国内外经济管理类各专业学生教学大纲中必不可少的公共基础课，是向学生传授随机现象及其规律，培养学生使用随机思想分析问题能力的重要途径［1－2］。很多其他后续课程，如统计学、证券投资学、信息论、密码学等都需要以概率统计知识为前提。经济管理专业学生毕业后大多从事经济贸易、金融投资、银行、证券、保险等工作，在工作中会遇到许多随机现象，如证券价值的变动、购买保险的人数、商品的库存和收益等，这些工作的完成也需要依赖概率统计知识［3－11］。因此，让学生轻松、愉快的学好这门课程成为了摆在每个老师面前亟待解决的问题。

不少学生在刚开始学习概率统计，尤其是初遇古典概型时，很有兴趣，也能够联系实际主动思考，但随着后续知识中公式、定理的逐渐增多，他们认为越来越枯燥，以致越学越没有兴趣，这一点应值得重视和思考。概率统计的思想方法来源于生活，教学中应处处有案例，从贴近生活或与学生专业相关的问题入手，用身边常见的现象和例子说明问题，从问题到理论，再从理论到应用，而不是生硬的从概念到理论，不仅可以激发学生的学习热情，减少距离感，强化实践意识，提高学生分析问题和解决问题的能力，还可以拓展学生的视野，从而提高学习的兴趣与效率［12－14］。

下面选取概率统计中有代表性的4个知识点，提出贴近现实、清晰易懂的案例，引导学生积极思考，自主求解，变被动学习为主动学习。

1 条件概率与三门问题

这个问题来自于美国的一个电视节目，参与者会看见3扇关闭了的门，其中1扇的后面有1辆汽车，选中后面有车的那扇门就可赢得该汽车，另外2扇门后面则各藏有1只山羊。当参与者选定了1扇门，但未去开启它的时候，节目主持人开启剩下2扇门的其中1扇，露出其中1只山羊。随后主持人问参与者要不要改选另1扇仍然关上的门。需要思考的是：改选另1扇门会不会增大参赛者赢得汽车的机会。

这个有趣的问题提出后，一定会引发学生热烈的讨论。这一问题的答案是——应该换，但是许多学生都想不通，他们认为换不换一样，赢得汽车的概率都是1／3。实际上，问题的关键在于主持人，不应该忽略这样一个线索，即主持人一定会开启1扇没有汽车的门。使用条件概率的思考方法就可以解决这个问题。

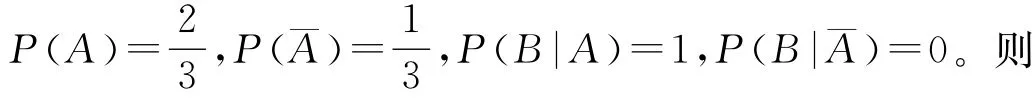
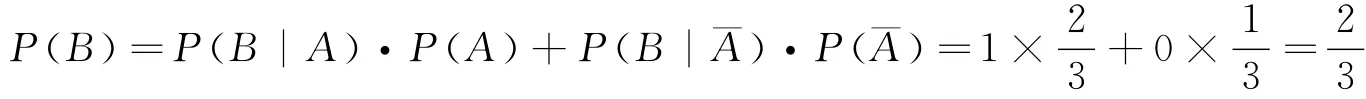
也就是说，如果坚持原来的选择，赢得汽车的机会是1／3，而选择另1扇门，赢得汽车的机会增加到了2／3，所以应该改变原来的选择。

可以进一步思考，若主持人事先不知道任何信息，而是随机开启某1扇门，即打开的1扇门之后有可能是汽车，也有可能是山羊，那么问题的答案是否会改变呢。

2 全概率公式与囚徒的智慧

在现实的各种领域，如经济、医学、生产等方面，常常会涉及到各种概率问题，但这些事件会有各种类型的条件限制和复杂的样本空间，导致在计算概率时，思路不清晰，甚至重复或遗漏了某些情况发生的可能性。全概率公式应运而生，能够化繁为简。以一个古代小故事为例来说明这个问题。1名囚犯要被执行死刑，按照传统，执行死刑前还有一次机会。在囚犯面前放2个一样的盘子，每个盘子盛有14个球，黑白颜色各一半。令囚犯蒙住眼睛从2个盘子中随机选1个，再从选中的盘子中随机选1个球，若选中白球则获得赦免，否则继续执行死刑。聪明的囚犯略思索后，要求将其中1个盘子里放2个白球，其余的球都放在另1个盘子中。问该囚犯获得赦免的机会比原来增加多少。令事件A为囚犯选中白球，事件B为囚犯选中第一只盘子。按照传统的分球方法，即每个盘子盛有14个球，黑白颜色各一半时，

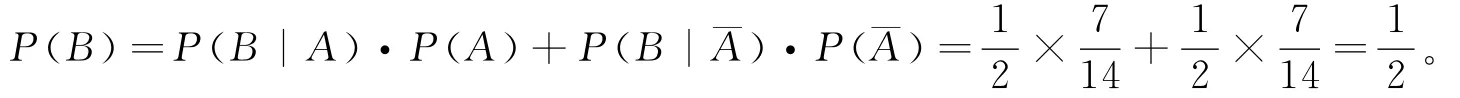
若按照囚犯提出的要求，即第一只盘子放2个白球，第二只盘子盛有其余26只球，则

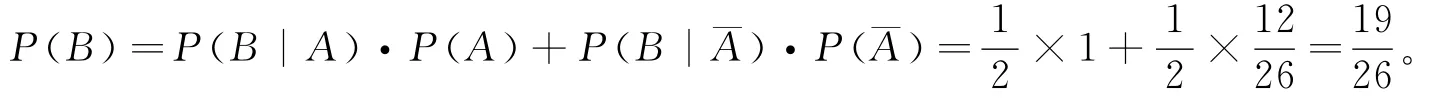
这样，聪明的囚犯通过争取，将自己获得生还的机会增加了3／13。进一步，可以向学生提出思考题，能否通过改变球在盘子中的分配方法，使得囚犯的生还机会变得更大。

3 数学期望与赌金分配

1654年，赌徒德·梅累向法国数学家帕斯卡提出一个使他苦恼很久的分赌本问题：甲、乙2赌徒赌技相同，各出赌注50法郎，每次赌局中无平局。他们约定，谁先赢3局则得到全部100法郎的赌本。当甲赢了2局，乙赢了1局时，因故要中止赌博。现问这100法郎如何分才算公平。

事实上，很容易设想出以下2种分法：

1）考虑到甲、乙2人赌技相同，平均分配赌金：即甲得50法郎，乙得50法郎。这种分法没有照顾到甲已经比乙多赢1局这个现实，对甲显然是不公平的。

2）考虑到已经进行的3局比赛结果，按照赌局输赢次数的比例分配赌金：甲得200／3法郎，乙得100／3法郎。这种分法没有考虑到如果继续比下去的话会出现什么情形，即没有照顾2人在现有基础上对比赛结果的一种期待。

那么，这更合理的第3种分法又该怎样分呢？提醒学生思考如果赌局进行下去，会出现的情况：最多只需再赌2局即可结束这场赌博。而再赌2局可能出现的所有结果以有序对表示，如（甲，乙）表示第一场赌局甲赢，第二场赌局乙赢。由于2人赌技相同，这4种情况出现的概率应相等，2场赌局结果的分布概率如表1所示。

表12 局结果及概率分布

如前3种结果发生，都是甲先赢3局，即甲赢得全部赌金100法郎，相应的概率为3／4，而甲得0法郎的概率为1／4，故甲获得的期望赌金为

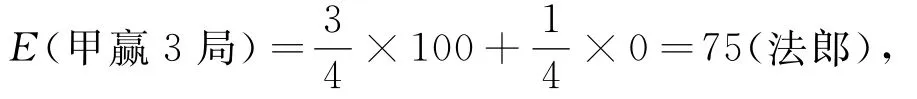
而乙应分得25法郎。因此，既考虑到甲已经比乙多赢一局的事实，又考虑到后续可能出现的结果，按照数学期望的思想分配赌金是比较公平的。

在这个故事中，出现了“期望”这个词，也是“数学期望”这个术语名称的由来。分赌本问题的思想可以进行推广，例如应用到投资问题：甲乙2人合资办厂，经营一段时间后，甲乙2人都要单独经营或者由于某种原因不能继续合作下去，应该怎样分配经营成果；或者因为经验不善而亏损，应该如何分摊债务等相关问题。这些思考对于经管相关专业的学生是有所裨益的。

4 大数定律与保险经营

概率法则总是在对大量随机现象的考察中才能显现出来，为了研究“大量”的随机现象，常常采用极限的形式，这就引导到极限定理的研究。大数定律就是极限定理研究的成果之一。所谓大数定律，即是用来说明大量的随机现象由于偶然性相互抵消所呈现的必然数量规律的一系列定理的统称。大数定律的运作，可以将个别风险单位遭遇损失的不确定性，转化为风险单位集合的损失的确定性。由于与损失金额的预测具有相关性，大数定律的运用直接关系到补偿或给付的实现程度与保险经营的稳定性［15］。

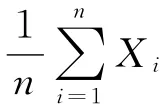
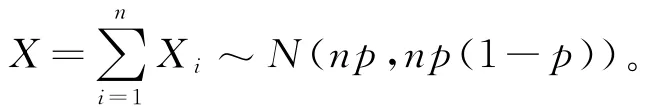
例如，假设保险的损失概率为0.2，置信水平为1－α＝0.95，当参保人数为100人时，实际损失变动与保险单位总数的比值为

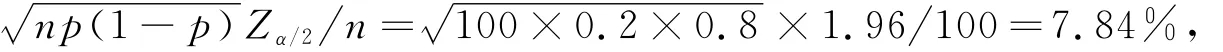
但若参保人数达到10000人时，该比值则降低到

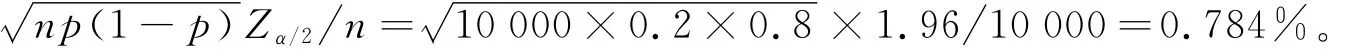
反之，保险公司可以从控制风险的角度，先制定实际损失变动与保险单位总数的比值，进一步从中确定该项保险的最低参保人数。

5 结 论

在概率论与数理统计的课堂教学中有针对性的提出问题，营造一个积极思考的环境，有助于帮助学生了解概率统计的方法来源于实际，又在实际工作中有广泛的应用。能够引导学生一步一步自己寻求解决问题的方法，激起学生的探究欲望，而不是被动地记忆、理解教师传授的知识。在解决案例的过程中，学生可以获得亲身思考的机会，便于逐渐形成善于质疑、乐于探究、勤于动脑、努力求知的研究态度。

［1］盛骤，谢式千，潘承毅.概率论与数理统计［M］.北京：高等教育出版社，2010.

［2］茆诗松，程依明，濮晓龙.概率论与数理统计教程［M］.北京：高等教育出版社，2004.

［3］张艳辉.保险经营中的大数法则与规模经济性［J］.财贸研究，2003，14（3）：36-38.

［4］鲍如钧，李聪.基于概率模型的证券投资定量决策支持［J］.上海海运学院学报，2002，23（1）：77-82.

［5］戴振强.证券投资决策的概率方法［J］.2007，23（5）：9-10.

［6］唐万生，梁建峰，韩其恒.组合证券投资的概率准则模型［J］.系统工程学报，2004，19（2）：193-197.

［7］刘裔宏，王毓基.关于保险理赔的概率分析［J］.系统工程，1992，10（3）：35-40.

［8］叶其宏.一种改进的概率密码方案的构建与分析［J］.浙江海洋学院学报：自然科学版，2007，26（3）：303-306.

［9］王新春，肖继先，刘晓红.案例在概率论教学中的应用［J］.河北理工大学学报，2007，10（2）：105-107.

［10］李强，张文倩.跨专业概率统计案例教学与实践探索［J］.泰山学院学报，2009，31（3）：140-144.

［11］马金凤，汤骅.将数学史及实际案例融入概率统计课程的教法研究［J］.数学教学研究，2010，29（4）：57-60.

［12］徐群芳.概率论与数理统计课程教学的探索与实践［J］.大学数学，2010，26（1）：10-13.

［13］刘琼荪，钟波.将数学建模思想融入工科“概率统计”教学中［J］.大学数学，2006，22（2）：152-154.

［14］杨静，陈冬，程小红.贝叶斯公式的几个应用［J］.大学数学，2011，27（2）：131-132.

［15］王东红.大数定律和中心极限定理在保险业中的重要应用［J］.数学的实践与认识，2005，35（10）：128-133.

Exploration of case teaching method in probability and statistics course

WANG Xin，CHENG Ximing

（College of Science，Beijing Information Science＆Technology University，Beijing 100192，China）

Probability and Statistics is not only a required course for mathematics major but also a basic course for majors in economic management and engineering.It closely combines theory with practice and is characterized by wide coverage and great applicability.Case teaching method，as a means of teaching reform，is applied to the classes of Probability and Statistics with focus on four important knowledge points as follows，conditional probability，total probability formula，mathematical expectation and law of large numbers.Some practical cases in the daily life are first introduced to students before a detailed process of problem solving is presented，thus stimulating their curiosity and ability to explore problems and familiarizing them with the application of probability and statistics knowledge in their real life.Class experiments have clearly shown that case teaching method is much significance to broaden students'vision，better the curriculum construction，enhance teaching effects，and improve the capability of teachers and students.

cases-driven；total probability；mathematical expectation；law of large numbers；confidence interval

O212.1

A

10.3969／j.issn.1673-5862.2013.03.014

1673-5862（2013）03-0372-04

2012-10-12。

北京市委组织部优秀人才项目（2011D005007000005）；北京信息科技大学教学改革基金资助项目（2011JGYB45）。

王 昕（1978-），女，河北邯郸人，北京信息科技大学讲师，博士。

book=375,ebook=113