关于局部α次积分C-半群的一些性质

李 静，赵华新

（延安大学数学与计算机学院，陕西延安 716000）

关于局部α次积分C-半群的一些性质

李 静，赵华新

（延安大学数学与计算机学院，陕西延安 716000）

算子半群的基本理论是泛函分析的一个内容丰富的重要分支。1987年Adrendt首先提出了一次积分半群，并且对一次积分半群的性质进行了讨论。1988年，Neubrander首次引入了n次积分半群的概念，随着研究的进一步深入，又出现了积分C-半群，n次积分C-半群，α次积分C－半群，局部n次积分C-半群及局部α次积分C-半群等，其中郑权对α次积分C-半群的扰动做了深入的研究，这为后来学者对局部α次积分C-半群的研究奠定了基础。在上述理论的基础上，利用局部α次积分C-半群的定义，并且结合α次累积分及卷积性质，得出局部α次积分C-半群的几个性质定理。

局部α－次积分C-半群；生成元；次生元

0 引 言

算子半群是泛函分析的一个重要分支，Adrendt、Neubrander对积分半群进行了讨论［1－2］。文献［3-16］主要讨论了C-半群的相关问题。本文主要参考郑权对α次积分C-半群扰动问题的研究，给出局部α次积分C-半群的几个性质定理。

1 预备知识

定义［3］设α≥0，｛S（t）｝0≤t＜T是X上的局部α次积分C-半群，A是闭线性算子，如果：

则称A生成局部α次积分C-半群｛S（t）｝0≤t＜T，此时A成为｛S（t）｝0≤t＜T的次生元。

在下述结果中，X是Banach空间，所有算子均是线性算子，B（X）是X上的所有线性算子构成的Banach空间，C∈B（X），设T＞0，α＞0及n∈N使得n－1＜α≤N。

2 主要结果

定理A生成局部α次积分C-半群｛S（t）｝0≤t＜T，则下列结论成立：

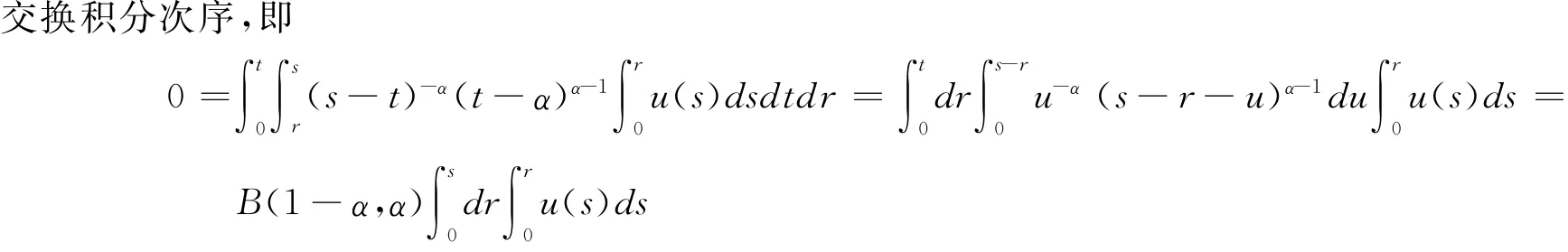
两边关于s两次求导得u（s）＝0；

当α＞1时，则可通过微分转化成0＜α≤1的情形；

综上可知u（t）＝0，t∈［0，T）。

3 结 论

文章在局部α次积分C-半群的基础上，利用α次累积分及卷积性质，得出局部α次积分C-半群的几个性质定理，使得算子半群理论的研究内容更加丰富。

［1］ADRENDT W.Vector-valued Laplace transforms andCauchyproblems［J］.Isral J Math，1987，59：327-352.

［2］NEUBRANDER F.Integrated semigroups and their applications to theAbstractCauchy problem［J］.Pacific J Math，1988，135（1）：111-137.

［3］窦丽娜，赵华新，乔华玲.局部弱α次积分C-存在族与抽象Cauchy问题（Ⅱ）［J］.延安大学学报：自然科学版，2004，23（2）：4-7.

［4］刘清荣，桂小风.关于积分C-半群的几点性质及其对抽象Cauchy问题的应用［J］.西北大学学报：自然科学版，1994，24（1）：1-5.

［5］高峰，赵华新.广义C-半群的生成元和性质［J］.沈阳师范大学学报：自然科学版，2012，30（2）：137-140.

［6］朗开禄.关于积分半群与积分C-半群扰动的两个结果［J］.楚雄师范学院学报，2005，20（6）：7-8.

［7］郑权.一类高阶抽象Cauchy问题及其应用［J］.应用泛函分析学报，1993，16（3）：319-327.

［8］孙正国.α次积分C-半群与抽象Cauchy问题［J］.数学学报，1999，42（4）：757-762.

［9］ZHENG Quan.Perturbations and Approximations of Integrated Semigroups［J］.Acta Math ematica Sinica，1993，9（3）：252-260.

［10］陆凤玲，宋小秋，王甫红.α次积分半群的扰动［J］.应用泛函分析学报，2010，12（3）：244-258.

［11］张宏伟，梁本中.抽象Cauchy问题与α次积分C-半群［J］.信阳师范学院学报：自然科学版，1994，7（1）：111-117.

［12］WANG Shengwang.Mild IntegratedC-existence Families［J］.Studia Math，1995，112（3）：251-266.

［13］赵华新.局部积分C-半群与抽象Cauchy问题［J］.延安大学学报：自然科学版，1985，14（1）：1-8.

［14］黄永忠.局部C-存在族与抽象Cauchy问题的解［J］.内江师专学报，1995，10（2）：1-7.

［15］王彩侠，宋晓秋，曹德侠.局部n次积分C-半群与一类抽象Cauchy问题C的适定性［J］.中国矿业大学学报，2004，33（3）：356-359.

［16］秦喜梅.局部n次积分C-半群与抽象Cauchy问题［J］.巢湖学院学报，2011，13（3）：13-16.

Some properties about localα-times integratedC-semigroups

LI Jing，ZHAO Huaxin
（School of Mathematics and Computer Science，Yan'an University，Yan'an 716000，China）

The basic theory of the operator semigroups is an important branch of functional analysis.In 1987，the integrated semigroups and its properties were first proposed and explored by Adrendt.In 1988，the concept ofn-time integrated semigroups was first introduced by Neubrander.With further research，integratedC-semigroups，n-time integratedC-semigroups，α-time integratedC-semigroups，localn-time integratedC-semigroups，localα-time integratedC-semigroups，etc have appeared successively.Zheng Quan researched the perturbations ofα-time integrated semigroups，which laid the foundation for the later scholars studying localα-time integratedC-semigroups.According to the definition of localα-time integratedC-semigroups，and combining with the properties ofα-time repeated integral and convolution formula obtained，some theorem of localα-time integratedC-semigroups are given.

localα-times integratedC-semigroups；generator；sub-generator

O177

A

10.3969／j.issn.1673-5862.2013.02.022

1673-5862（2013）02-0236-03

2012-12-17。

陕西省教育厅专项科研计划项目（12JK0891）。

李 静（1987-），女，陕西横山人，延安大学硕士研究生；赵华新（1964-），男，陕西延安人，延安大学教授，硕士研究生导师。