客运专线拱桥承台设计方法的探讨

李 宇

(铁道第三勘察设计院集团有限公司桥梁处,天津 300142)

1 概述

2 精细有限元分析

图1 双线客运专线拱桥的桩基承台(单位：cm)

图1为某客运专线上承式拱桥桩基承台。首先进行精细有限元模拟，将土体、桩对承台的影响都考虑进模型，再根据有限元结果进行配筋。并通过分析应力云图明确承台底面、承台拱脚相交截面的受力特征，进而采用符合其受力特征的规范公式进行检算[3]。

承台有限元模型按实际尺寸、材料建立，并模拟土体对桩侧、桩底的作用。利用Ansys三维实体单元Solid45建立混凝土单元及土体单元，利用Targe170、Contal173单元模拟桩与土体的接触面。根据圣维南定理，为消除局部加载对承台表面应力分布的影响，将荷载分别施加在高度1 m的加载平台上。建立模型所用承台-桩单元、土体单元、接触单元如图2所示。

图2 承台-桩-土模型

承台底部正应力云图见图3、图4。从图3可以看出，Y向正应力因桩顶反力产生了应力集中，在距离拱脚最近的一排桩处最大，其最大拉应力为5.08 MPa。从图4可以看出，承台底部X向正应力在最外两排桩之间为拉应力，承台底部中心靠近拱脚侧拉应力最大，最大拉应力为3.14 MPa。由模型计算结果可知承台底部与悬臂板受力趋势相同，可按受弯构件[4]检算配置的钢筋。

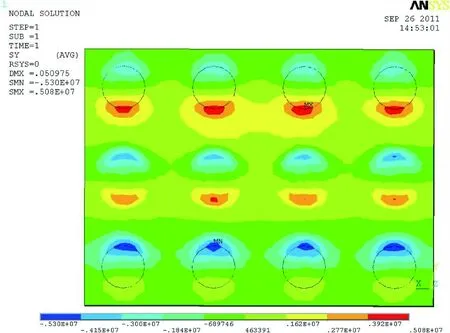
图3 承台板Y向应力云图

图4 承台板X向应力云图

承台与拱脚交面正应力云图见图5、图6。从图5可以看出，拱脚反力引起的Y方向正应力在承台表面最大，最大拉应力为8.13 MPa；拉应力向承台底部扩散，有效扩散深度达1.2 m。从图6可以看出，拱脚反力引起的Z方向正应力在承台表面最大，最大拉应力为6.60 MPa；拉应力向承台底部扩散，有效扩散深度达0.8 m。由模型计算结果可知，在拱肋传递的轴力及弯矩作用下承台表面与拱肋相交处承受较大的剪力，受力特征接近于冲切构件，可按冲切构件验算其配筋。同时应力影响深度较大，需要配置等深度的钢筋网来承担剪力并分散应力集中。

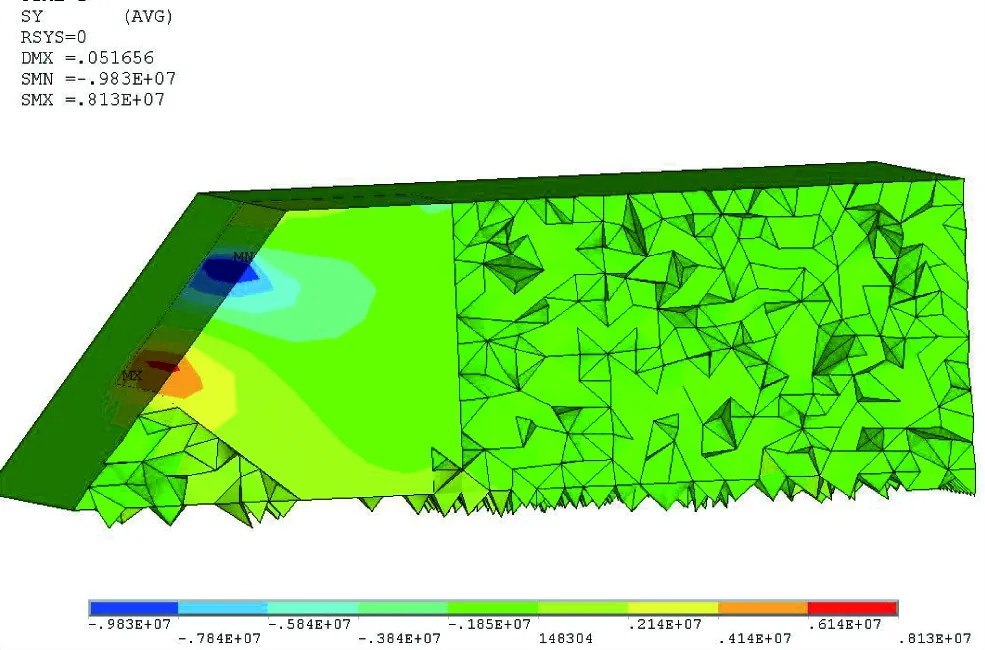
图5 承台拱脚截面Y向应力云图

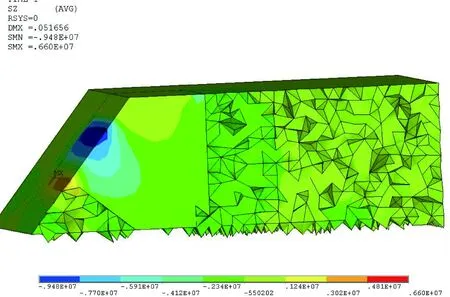
图6 承台拱脚截面Z向应力云图

利用有限元应力云图配筋，结果如下：承台底面A-A截面配置424φ28 mm钢筋，B-B截面配置227φ28 mm钢筋；拱脚截面(表层40 cm深度内)顺桥向、横桥向均配置24φ28 mm/m钢筋。

3 利用现行承台设计理论验算

拱桥承台计算除传统的承台底面配筋外，还要对承受强大反力的拱脚位置进行细部计算。关于承台底部的配筋检算基本可以分为“梁式体系”和“撑杆-系杆体系”2种计算方法，铁路桥梁设计中针对刚性角超过35°的承台板，通常按照钢筋混凝土构件进行检算，而对于拱脚位置可按冲切构件进行计算。

3.1 “梁式体系”计算方法

“梁式体系”为国内的建筑行业规范所采用，是传统的承台板计算方法，而对于铁路承台板构件来说，其构件的截面应力分布已经不遵循简单的平截面假定，这类构件称为“深梁”[5]。根据《铁路桥涵地基和基础设计规范》(TB10002.5—2005)[6]，对图1所示的桩基进行桩基内力计算，求得承台底处各桩顶反力；将承台板两悬臂模拟为简支梁，根据《混凝土结构设计规范》(GB50010—2002)[7]规定，跨高比l0/h≤2的简支梁或跨高比l0/h≤2.5的连续梁定义为“深梁”[8]，其正截面受弯承载力应符合下列规定

古汉语中，有些词语虽然本身已经有自己的文字，但有时写这个字或者用这个字时会用声音相同或者相近的汉字来替代。这种现象叫做 “假借”，这个替代原来本字的汉字就是“通假字”。[1]成语中，用字通假现象较为常见，如：

M≤fyAsz

z=αd(h0-0.5x)

αd=0.8+0.04l0/h

当l0

式中fy——普通钢筋抗拉强度设计值；

As——受拉区纵向非预应力钢筋的截面面积；

x——截面受压区高度，当x<0.2h0时，取x=0.2h0；h0为有效高度，h0=h-as，其中h为截面高度；当l0/h≤2时，跨中截面取as=0.1h，支座截面取as=0.2h；当l0/h>2时，as按受拉区纵向受拉钢筋截面重心至受拉区边缘的距离。

以上计算方法为规范规定的深受弯构件计算方法。由实体模型计算结果可知承台板与悬臂板受力趋势相同，可按受弯构件配置钢筋。其校核结果见表1。

表2 底面按受弯构件验算结果

3.2 冲切构件计算方法

承台是将桥梁上部荷载传递给桩基的重要构件，而拱肋的反力传递到承台表面相当于对承台与拱肋的交面处的钢筋及混凝土施加了巨大的剪力，其受力性能接近于冲切构件[9]。可按照《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG D62—2004)[10]中冲切构件计算其配筋。首先按照素混凝土板计算其抗冲切承载力

γ0Fld≤(0.7βhftd+0.15σpc,m)Umh0

式中Fld——最大集中反力设计值；

σpc,m——设有预应力钢筋的板截面上，由预加力引起的混凝土有效平均压应力；

βh——截面高度尺寸效应系数；

Um——距集中反力作用面h0/2处破坏椎体截面面积的周长；

h0——板的有效高度。

按照上式计算可得素混凝土板的抗冲切反力。若小于拱肋的轴向集中反力则按照配置抗冲切钢筋计算抗冲切承载力，可按下式计算

γ0Fld≤(0.35βhftd+0.15σpc,m)Umh0+0.75fsvAsvu

式中fsv——钢筋抗拉强度设计值；

Asvu——与冲切破坏锥体斜截面相交的全部钢筋截面面积。

承台拱脚截面按冲切构件方法计算的配筋结果如下：顺桥向、横桥向均配置17φ28 mm/m钢筋。

4 计算结果的比较

(1)采用有限元模型应力结果对承台底面进行配筋，再通过规范公式计算钢筋应力及混凝土裂缝是否满足要求。通过表1可见有限元与规范结果可以相互验证，证明有限元模型的正确性和对于承台底面配筋2种方法都适用。

(2)对承台拱脚截面采用有限元法与规范法分别计算钢筋用量，通过对比可见2种方法结果相差较大，有限元方法计算结果偏于安全，并可考虑不同方向配筋的变化；规范对于拱脚下配置钢筋网没有明确的计算方法，以往只能根据经验配筋，但有限元分析可以定量布置不同深度的钢筋网，对于设计有较好的指导作用。

5 结论

上承式拱桥承台由于其受力的特殊性，无法直接按规范计算配筋。首先采用有限元法计算，并为了反映承台的实际应力分布精细模拟了承台-桩-土的相互影响。再通过分析不同截面的受力特性采取相应的规范公式进行验算。通过比较发现有限元法的结果考虑了桩-土的非线性作用和拱肋引起应力集中、应力扩散对配筋的影响配筋结果更加安全，因此本设计最后采用有限元法的配筋结果。

[1] 林亚超，编译.承台板的应力分析与设计[J].国外桥梁，1981(3)：21-25．

[2] 铁道第三勘察设计院.铁路工程设计技术手册-桥涵地基和基础[M].北京：中国铁道出版社，2002.

[3] 李敬增.客运专线铁路承台板设计若干问题的探讨[J].铁道标准设计，2007(2)：60-62.

[4] 娄宇欣.客运专线桥梁承台板配筋设计的探讨[J].铁道标准设计，2010(9)：56-59.

[5] 王恩惠，译.厚承台设计[J].国外桥梁，1984(3)：32-35.

[6] 中华人民共和国铁道部.TB 10002.5—2005 铁路桥涵地基和基础规范[S].北京：中国铁道出版社，2005．

[7] 中华人民共和国建设部.GB50010—2002 混凝土结构设计规范[S].北京：中国建筑工业出版社，2002．

[8] 刘明君，粟怀广.钢筋混凝土承台配筋设计理论的探讨[J].铁道标准设计，2004(10)：7-8.

[9] 张天明.承台的配筋问题探讨[J].铁道标准设计，1991(2)：78-79.

[10] 中华人民共和国交通部.JTG D62—2004 公路钢筋混凝土及预应力混凝土桥涵设计规范[S].北京：人民交通出版社，2004.