使用B样条无单元法进行梯形盖板受力分析
2013-01-17李彬
李 彬
(中铁第四勘察设计院集团有限公司,武汉 430063)
钢筋混凝土梯形盖板大量应用于既有铁路斜交涵洞中,板厚与跨度比一般在0.1~0.25,属中厚板,在既有线改造或增建二线工程中,需要一种快速有效的方法对此类结构进行受力分析与评估。有限元法[9]是分析中厚板的有效方法,它通用性强,精度高,但是由于有限元法一般采用分片低阶多项式插值来逼近问题的解函数,在边界上一般只能达到C0连续,从而不可避免地造成了自由度多、工作量大的局面。许多学者将半解析法用于中厚板分析[10-11],取得了较好的效果。本文介绍了利用B样条无单元方法进行涵洞出入口钢筋混凝土梯形盖板受力分析的研究及其Matlab[12]实现。
1 基本方程

图1 梯形盖板示意
如图1所示,考虑一个在x-y平面内的等厚梯形盖板i-j-k-1,其中a为梯形盖板短边长、b为盖板长边长,L为计算跨度,t为厚度。i-j、k-1为自由边,i-1、j-k为简支边。
板的位移包括了3个分量:第一个是沿z方向的位移w,第二个是沿y轴方向的转角θx,第3个是沿x轴正方的转角θy。采用中厚板理论进行分析[9],面外剪应变及面内应变可分别表述为
γ=γxz
γyz=∂w∂x
∂w∂y-θx
θy≡w-θ(1)
ε=εx
εy
γxy=-z∂∂x0
0∂∂y
∂∂y∂∂x·θx
θy≡-zLθ(2)
设板厚为t,杨氏模量为E,剪切模量为G,泊松比为ν,则其应变能可表示为
int=1(Lθ)TD·((Lθ)·dΩ+
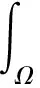
其中
D=Et312(1-ν2)α=56Gt
采用变分原理[13],式(3)的变分形式为


2 样条无单元法刚度列式的推导
将整个区域映射为在自然坐标(ξ,η)上的单位正方形,在此区域内对竖向位移采用双四次B样条进行拟合,对转角采用双三次B样条进行拟合,近似公式如下
w=∑q,rBq,4(ξ)·Br,4(η)·a(q,r)=
[B4(ξ)⊗B4(η)]·{a}(5)
θx=∑q,rBq,3(ξ)·Br,3(η)·bx(q,r)=
[B3(ξ)⊗B3(η)]·{bx}(6)
θy=∑q,rBq,3(ξ)·Br,3(η)·by(q,r)=
[B3(ξ)⊗B3(η)]·{by}(7)
其中,Bk,d为d次B样条的基函数;
Bd(ξ)=[B0,d(ξ),B1,d(ξ),B2,d(ξ),…,Bn,d(ξ)];
Bd(ξ)⊗Bd(η)为Bd(ξ)与Bd(η)的张量积;
{a}、{bx}、{by}分别为对w、θx、θy进行拟合的系数向量
{a}=[…,a(q,r),…]T
{bx}=[…,bx(q,r),…]T
{by}=[…,by(q,r),…]T
下文中,记

{C}为进行受力分析时的基本未知量,相当于有限元法中的位移。
函数f关于(x,y)和(ξ,η)的导数的变换关系如下
∂f∂ξ
∂f∂η=∂x∂ξ∂y∂ξ
∂x∂η∂y∂η∂f∂x
∂f∂y=[J]∂f∂x
∂f∂y(8)
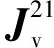
∂f∂x
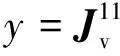

∂f∂η(9)
按式(2)有
Lθ=∂∂x0
0∂∂y
∂∂y∂∂x·θx
θy=∂θx∂x
∂θy∂y
∂θx∂y+∂θy∂x(10)
将式(9)代入上式






∂θx∂η
∂θy∂ξ
∂θy∂η(11)
使用式(6)、(7)的θx、θy插值公式,则上式成为



∂∂ξ[B3(ξ)⊗B3(η)]·{bx}
∂∂η[B3(ξ)⊗B3(η)]·{bx}
∂∂ξ[B3(ξ)⊗B3(η)]·{by}
∂∂η[B3(ξ)⊗B3(η)]·{by}=







bx
by=
[Bb]·{C}(12)
按式(1)、(9)有
w-θ=∂w∂x
∂w∂y-θx
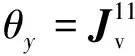

∂w∂η-θx
θy(13)
使用式(5)、(6)、(7)的w、θx、θy近似公式,则上式成为
w-θ

∂∂η[B4(ξ)⊗B4(η)]·{a} -
[B3(ξ)⊗B3(η)]·{bx}
[B3(ξ)⊗B3(η)]·{by} =



B3(ξ)⊗B3(η)0
0B3(ξ)⊗B3(η) ×
bx



bx
by-
0B3(ξ)⊗B3(η)0
00B3(ξ)⊗B3(η)·a
bx
by=



0B3(ξ)⊗B3(η)0
00B3(ξ)⊗B3(η)·{C}=
[Bg]·{C}(14)
利用式(12)、(14),式(4)可用离散形式表达为






(C)=δ(C)T·[K]·(C)(15)
其中[K]为刚度矩阵


3 等效荷载列式
对板上所施加的均布荷载q,其等效荷载列式按以下方式计算,列出其荷载势能的变分式
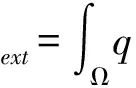
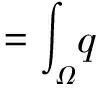
δB4(ξ)⊗B4(η)00·a
bx
by·dΩ=

等效荷载列式可表达为

4 边界条件
以在ξ=0边上施加软简支(SS1)边界条件为例,采用罚函数在整个能量泛函中加入一个修正项
penalty=12ρΓ(18)
其中为Γ简支边,对上式进行变分
δpenalty=ρ·δwξ=0Twξ=0dΓ=

B4ξξ=0⊗B4(η)·{a}dΓ=

B4ξξ=0⊗B4(η)00dΓ·(C) =
δ(C)T·Kpenalty·(C)(18)
求解时最后的刚度矩阵应为[K]+[Kpenalty]
5 算法的Matlab实现及验证
本方法中B样条节点在ξ、η方向上均匀分布,在ξ方向上有Kx+1列,在η方向上有Ky+1列,为减少节点数量,在首尾处的节点重复d次(d为B样条次数),即为所谓的开放均匀B样条,其系数向量的长度为(Kx+d-1)×(Ky+d-1),在竖向位移、转角分别采用双四次B样条和双三次B样条进行拟合的情况下,系统总的自由度数即的长度为
(Kx+3)×(Ky+3)+2×(Kx+2)×(Ky+2)
各节点坐标
(ξi,ηj)=(i/Kx,j/Ky)…i∈[0:Kx]j∈[0:Ky]
在样条节点所构成的网格背景上采用3点Gauss公式进行数值积分,以下将Gauss点称作样条的配点,利用Matlab样条工具箱中的spcol函数计算配点处样条的各阶导数值,计算张量积则使用kron函数。
由于样条无单元法具有算法简洁、后处理方便的特点,借助于Matlab样条工具箱的强大威力,开发的斜交梯形板分析程序仅用了不多300行的代码,开发效率高,后期维护方便。
为验证该算法的可靠性,计算了承受均布荷载的四边简支方板在不同厚度情况下的中心挠度与弯矩,并与文献[14]提出的RPAQ单元及解析解作了比较,结果见表1,表中q为均布荷载,a为方板边长,wc为方板中心点处的挠度,Mc为方板中心点处的弯矩,D为弯曲刚度。
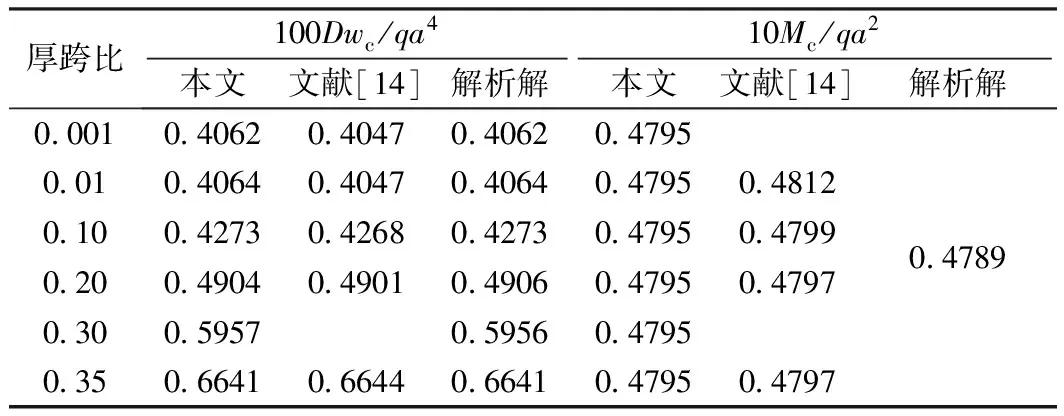
表1 不同厚度四边简支方板中心挠度与中心弯矩
计算时取μ=0.3,采用12×12分划的样条进行插值,RPAQ单元采用16×16的单元划分方式。从计算结果可以看出,本文算法不仅有着非常好的精度,而且没有剪切闭锁现象。
6 结论
本文提出了用于梯形盖板分析的B样条无单元法,详列了相关刚度矩阵推导的过程,说明了生成荷载列式与施加边界条件的方法。采用与文献中类似方法相比,对位移采用比转角高一次的B样条进行插值,不仅提高了精度,而且避免了板变薄时出现的剪切闭锁现象。
借助于Matlab及其Spline Toolbox编制了梯形盖板专用分析及评估程序,摆脱了此类结构分析完全依赖于大型通用有限元软件的局面,具有效率高、后处理方便的优点。通过对区域映射公式进行简单调整,该方法就可以推广到任意四边形的中厚板及薄板分析,具有一定的通用性。
[1] H.Antes. Bicubic fundamental splines in plate bending[J]. Int. J. Numer. Meth. Engng, 1974,8(3):503-511.
[2] Atluri S N, Zhu T L. New Concepts in Meshless Methods[J]. Int. J.Numer. Meth. Engng, 2000,47(1-3):537-556.
[3] Ahmed A. Shabana, Ashraf M. Hamed. Use of B-Spline in the Finite Element Analysis: Comparison With ANCF Geometry[J]. J.Comput.Nonlinear Dynam. Volume 7, Issue 1, 011008, 2012.
[4] 石钟慈.样条有限元[J].计算数学,1979(1):50-72.
[5] 何广乾,周润珍,林春哲.样条函数法在解板壳问题中的应用[J].建筑结构学报,1981,2(2).
[6] 朱明杈.解任意四边形板弯曲问题的样条有限元法[J].计算教学,1987(1):23-42.
[7] Fan, S. C. and Cheung, Y. K., Analysis of shallow shells by spline finite strip method[J], Engineering Structures, 1983,5(4):255-263.
[8] 刘效尧.样条单元族及其在桥梁结构中的应用[J].土木工程学报,1983(2):10-20.
[9] O. C. Zienkiewicz, R. L. Taylor. The Finite Element Method for Solid and Structural Mechanics[M]. Sixth Edition (Volume 2) Butterworth-Heinemann, 2005.
[10] 赵艳林.中厚板弯曲分析的样条函数方法[J].广西大学学报:自然科学版,1993(3):52-57.
[11] 沈小璞,何沛祥.样条有限元法解中厚度矩形板弯曲[J].安徽建筑,1996(S1).
[12] Eva Pärt-Enander. Anders Sjöberg.MATLAB5手册[M].北京:机械工业出版社,2000.
[13] 胡海昌.弹性力学的变分原理及其应用[M].北京:科学出版杜,1981.
[14] 龙驭球,陈晓明,岑松.一个不闭锁和抗畸变的四边形厚板元[J].计算力学学报,2005(8):385-391.
