南京市浦口滨江大道软土参数相关性分析

韩 旭，李少雄，丁 磊

(长江水利委员会长江岩土工程总公司(武汉)，湖北武汉 430010)

1 工程概况

根据南京市浦口区城市总体规划，浦口滨江大道是浦口新市区总体规划中重要组成部分，地处南京市西北部，长江北岸，与南京市雨花台区、江宁区隔江相望。建成后将串起长江大桥和长江三桥，总长约20 m，双向四车道，以观光、休闲、防汛为主的景观生态道路。

道路沿线广泛分布有长江近岸漫滩相软土地层，其强度低、厚度大、埋藏浅，对工程建设影响较大。因此，利用先进的勘察手段，科学分析该层软土的工程特性，为设计和施工部门提供准确合理的地基设计参数，具有非常重要的意义。

2 软土特征

2．1 软土的分布特征

南京市浦口滨江大道沿线软土地层主要分布有两层(图1):

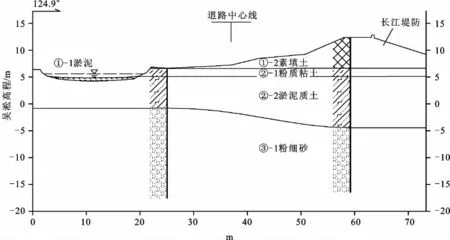
图1 浦口滨江大道典型地质剖面Fig.1 Typical geological profile of Binjiang Avenue

①-1层为新近沉积的淤泥，灰黑色，流塑状，夹有少量生物残骸，具腥臭味。该层零星分布在水塘、沟渠底部，一般厚度为0．3 ～1．5 m，局部厚度达2．5 m。

②-2层为淤泥质土，灰色、灰黑色，间夹薄层粉土或粉细砂，软塑状为主。该层广泛分布在工程沿线，分布厚度变化较大，一般为3．0～15．0 m，局部厚度达20 m，顶板埋深2．0～8．0 m。该层软土整体上具有两端薄、中间厚特征，即南京长江大桥和长江三桥附近该层软土的厚度相对较薄，一般为1～3 m，中间相对较厚，厚度一般为10～20 m。

其中②-2层淤泥质土为本文的主要研究对象。

2．2 软土的物理力学特征

经过对南京浦口滨江大道土工试验进行统计分析(表1、表2)，该层软土具有如下主要物理力学特征:

(1)天然含水率高、孔隙比大。天然含水率平均值37．0%，大于液限36．1%;天然孔隙比平均值1．089，最大值1．469，均＞1;天然饱和度平均值94%。

(2)压缩性大。平均压缩系数 0．64 MPa－1，＞0．5 MPa－1;平均压缩模量 3．5 MPa，＜ 5 MPa，属于高压缩性土。

(3)低透水性。平均渗透系数为3．43×10－6cm/s，具微透水性。

(4)抗剪强度低。天然快剪C值9．4 kPa、φ值7．1°;十字板剪切 CU平均值20．9 kPa;比贯入阻力 Ps平均值 0．32 MPa。

(5)灵敏度 St值为 3．2～5．2，属中等灵敏—灵敏［1］。

表1 软土主要物理力学参数统计Table 1 Statistics of main physical and mechanical parametes of soft soil

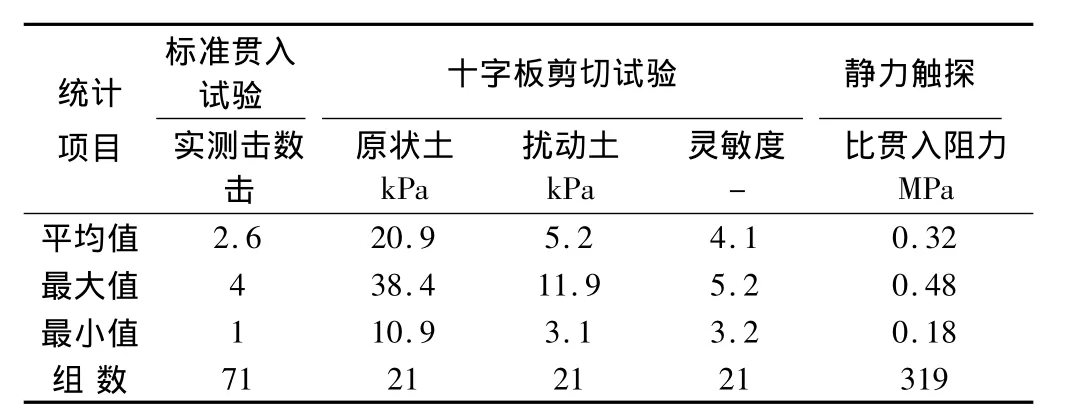
表2 软土原位试验成果统计Table 2 Statistics of in-situ test results

3 软土主要物理力学参数的相关性

采用SPSS分析软件［1］，对软土的主要物理力学参数进行一元线性回归分析，可获得各参数间的规律性关系，并建立地区性经验公式，通过较易取得的参数反演较难得到的参数，可以为该地区的工程建设提供借鉴。

相关性强弱的判别依据相关系数R的绝对值的大小，通常按下述标准进行:|R|＞0．8，显著相关性;0．8 ＞ |R|＞0．3，弱相关性;|R|＜0．3，无相关性。

3．1 主要物理参数间的统计关系

(1)含水率ω与孔隙比e的关系 根据土力学定义，孔隙比是土孔隙体积与固体颗粒的体积之比。一般认为，在地下水位以下的土是饱和的，孔隙比与含水率之间应表现为线性正比关系。

含水率ω与孔隙比e的关系散点图如图2所示，用最小二乘法进行数值分析，其回归方程如下:

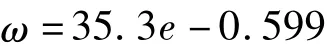
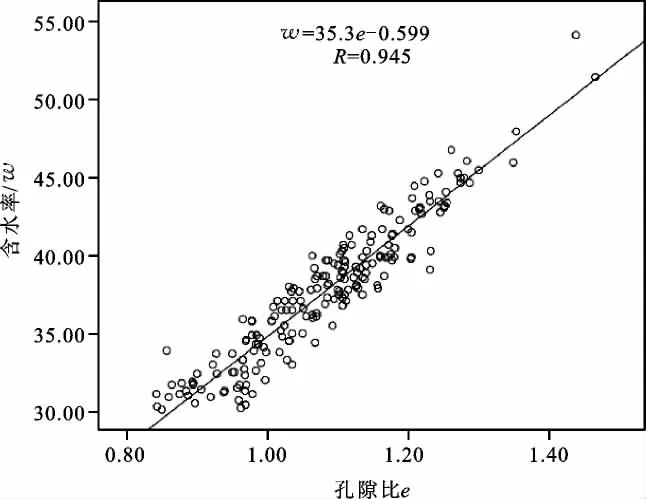
图2 含水率—孔隙比关系散点图Fig.2 Scatter diagram of relation between content and void ratio

上式二变量的相关系数达0．945，表明含水率和孔隙比之间具有非常显著的线性正相关性。

(2)含水率ω与密度ρ的关系 含水率与的密度关系见图3所示，其回归方程可表示为:

ω = －68．517ρ+161．027

上式二变量之间的相关系数为－0．711，表明含水率ω和密度ρ之间具有线性弱负相关性。

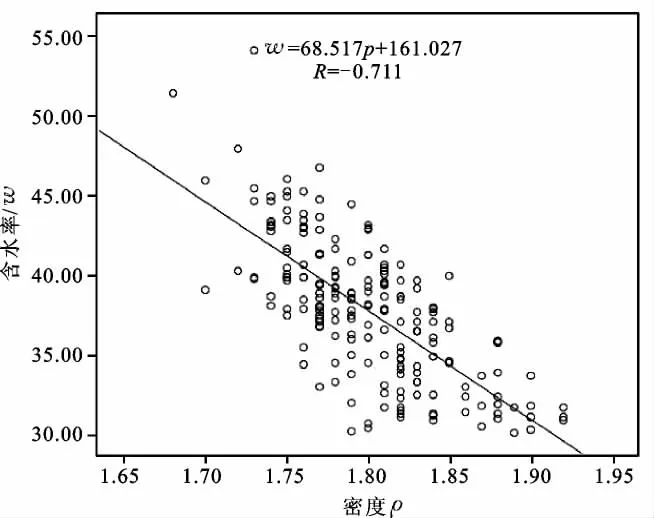
图3 含水率—密度关系散点图Fig.3 Scatter diagram of relation between water content and density

(3)孔隙比e与密度ρ的关系 孔隙比e和密度ρ的散点关系如图4所示，二变量的回归方程关系式为:

e= －2．361ρ+5．332

回归方程表明，孔隙比e和密度ρ之间为一种线性负相关关系，其相关系数为－0．902，相关性非常显著。

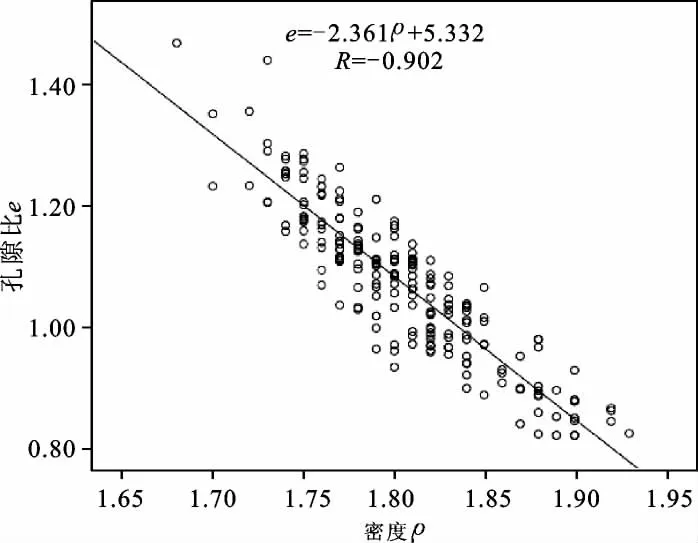
图4 孔隙比—密度关系散点图Fig.4 Scattcer diagram of relation between void ratio and density

3．2 主要物理参数与力学参数间的统计关系

(1)压缩系数αv与含水率ω的关系 压缩系数αv与含水率ω的散点关系如图5所示，两者之间的回归方程表达式为:

αv=0．024ω －0．311

由回归方程可见，其相关系数为0．766，压缩系数αv与含水率ω呈现一种线性弱正相关性。

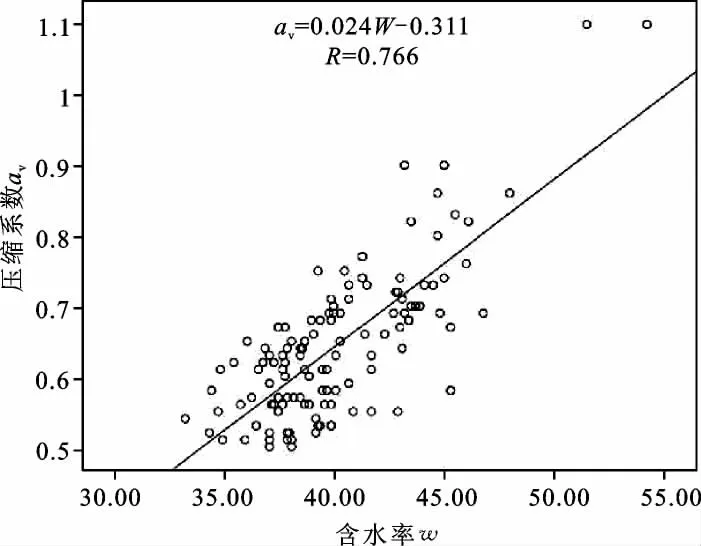
图5 压缩系数—含水率关系散点图Fig.5 Scatter diagram of relation between compressibility and water content

(2)压缩系数αv与孔隙比e的关系 压缩系数αv与孔隙比e的散点关系如图6所示，两者之间的回归方程表达式为:

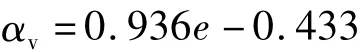
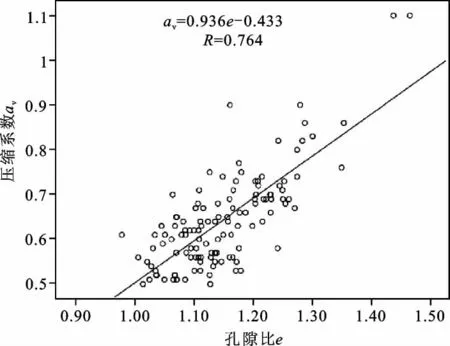
图6 压缩系数—孔隙比关系散点图Fig.6 Scatter diagram of relation between compressibility and void ratio

由回归方程可见，其相关系数为0．764，压缩系数αv与孔隙比e呈现一种线性弱正相关性。

(3)压缩模量Es与含水率ω的关系 压缩模量Es与含水率W的散点关系如图7所示，两者之间的回归方程表达式为:

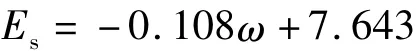
由回归方程可见，其相关系数为－0．723，压缩模量Es与含水率ω呈现一种线性弱负相关性。

(4)压缩模量Es与孔隙比e的关系 压缩模量Es与孔隙比e的散点关系如图8所示，两者之间的回归方程表达式为:

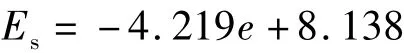
由回归方程可见，其相关系数为－0．749，压缩模量Es与孔隙比e呈现一种线性弱负相关性。

3．3 主要力学参数间的统计关系

(1)压缩系数αv与凝聚力C、内摩擦角φ的关系随着压缩系数αv的增加，凝聚力C、内摩擦角φ呈递减的趋势，如图9、图10所示。用最小二乘法来进行统计分析，压缩系数αv与凝聚力C的线性相关系数为－0．104，无相关性;压缩系数αv与内摩擦角φ的线性相关系数为－0．411，参数间属弱负相关性。压缩系数αv与内摩擦角φ相应的回归方程为:

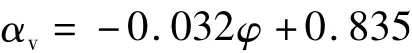
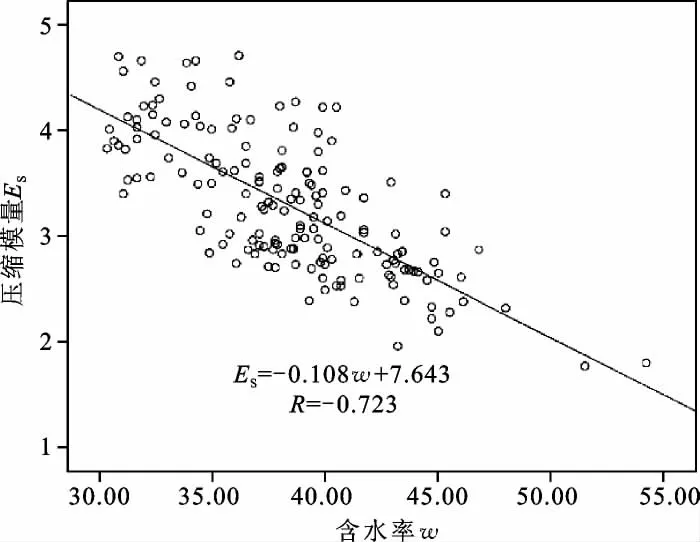
图7 压缩模量—含水率关系散点图Fig.7 Scatter diagram of relation between compression modulus and water content

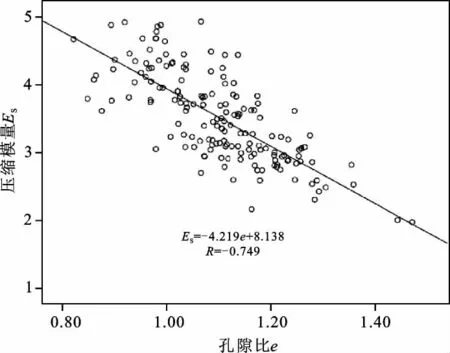
图8 压缩模量—孔隙比关系散点图Fig.8 Scatter diagram of relation between compression modulus and void ratio

(2)压缩模量Es与凝聚力C、内摩擦角φ的关系随着压压缩模量Es的增加，凝聚力C、内摩擦角φ呈递增的趋势，如图11、图12所示。用最小二乘法来进行统计分析，压缩模量Es与凝聚力C的线性相关系数为0．299，参数间无相关性;压缩模量Es与内摩擦角φ的线性相关系数为0．606，参数间属弱正相关性。压缩模量Es与内摩擦角φ相应的回归方程为:Es=0．183φ +2．251

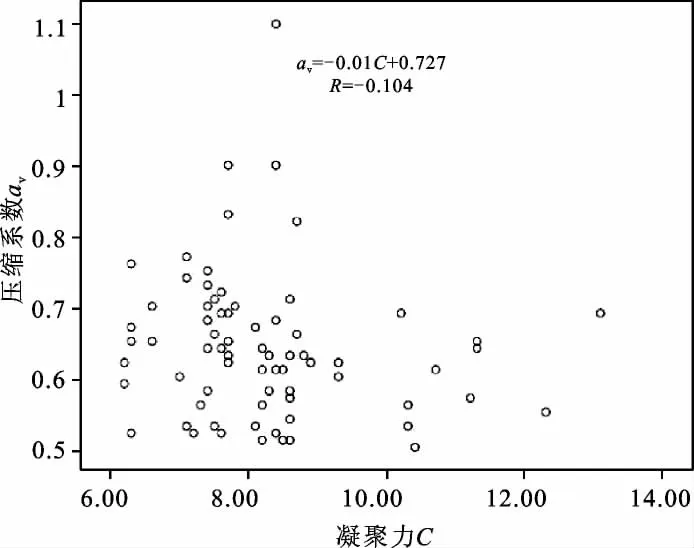
图9 压缩系数—凝聚力关系散点图Fig.9 Scatter diagram of relation between compressibily and cohesiveness

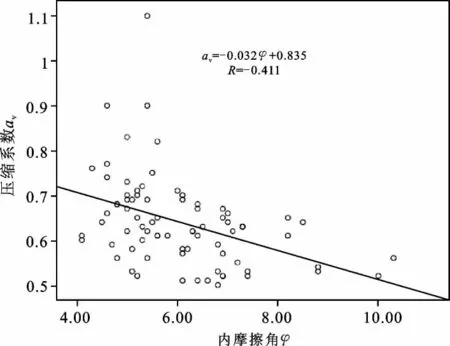
图10 压缩系数—内摩檫角关系散点图Fig.10 Scatter diagram of relation between compressibility and internal frictional angle

(3)凝聚力C与内摩擦角φ的关系 凝聚力C与内摩擦角φ的散点关系如图13所示，两者之间的回归方程表达式为:

C=0．512φ +5．262

由回归方程可见，其相关系数为0．627，凝聚力C与内摩擦角φ具有线性弱正相关性。

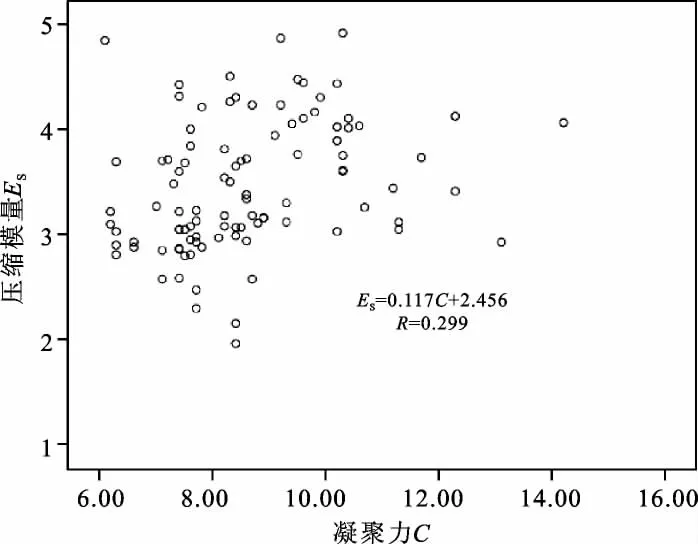
图11 压缩模量—凝聚力关系散点图Fig.11 Scatter diagram of relation between compression modulus and cohesiveness

4 主要物理力学参数随深度变化的统计分析

经一元线性回归统计分析，②-2层软土主要物理力学参数随深度变化的回归方程及相关系数见表3。

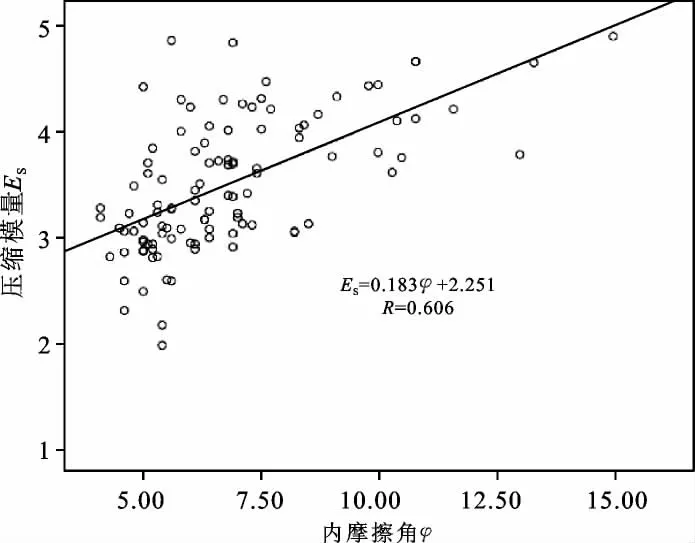
图12 压缩模量—内摩檫角关系散点图Fig.12 Scatter diagram of relation between compression modulus and internal frictional angle

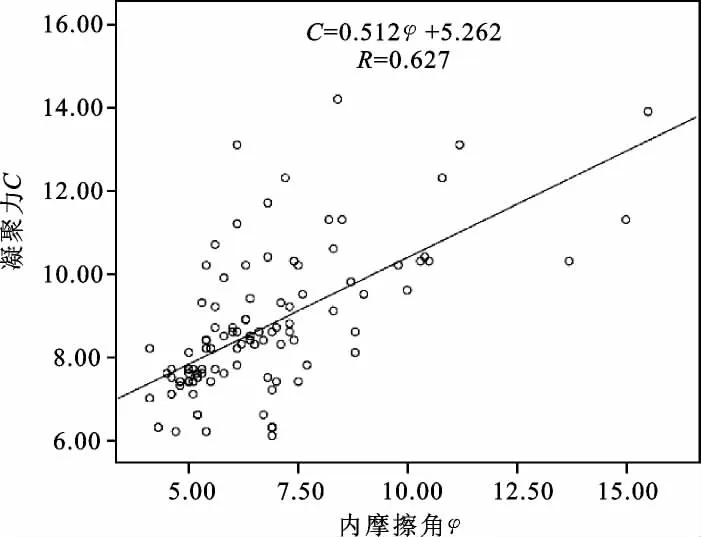
图13 凝聚力—内摩擦角关系散点图Fig.13 Scatter diagram of relation between cohesiveness and internal frictiond angle

由统计分析表明，随着取土深度增加，含水率、液限、液性指数呈递减的趋势，具线性弱负相关性，孔隙比、密度、塑限、塑性指数、压缩系数、压缩模量、凝聚力、内摩擦角与取土深度均无明显的相关性。

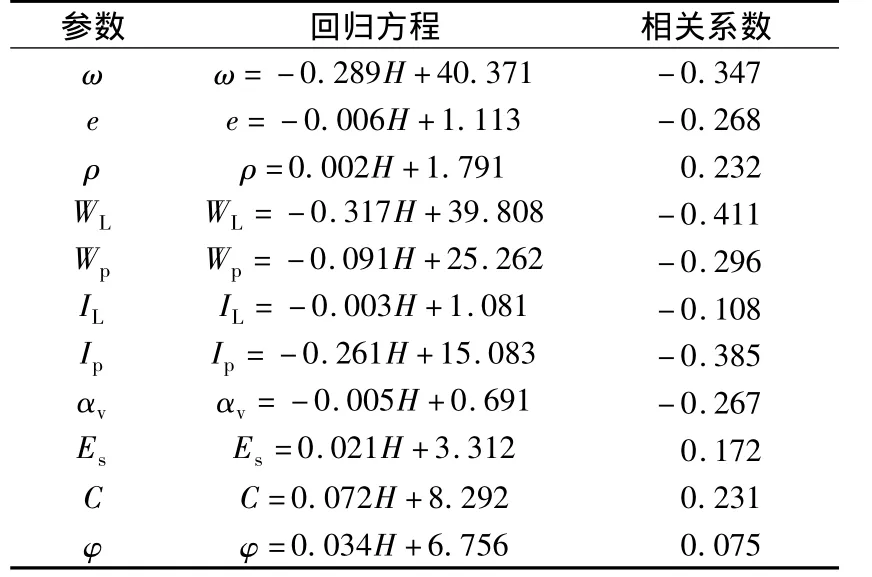
表3 主要物理力学参数随深度变化分析Table 3 Main physical and mechanical parameters with the change of depth

5 结论

本文对南京浦口滨江大道路基软土的分布、物理力学特征进行了系统的统计分析，并运用数值分析方法，分析了软土的主要物理力学性质参数间的相关性，对相关性较密切的参数间建立了回归方程，对于指导软土路基处理设计、工程施工，具有重要的理论与工程实际意义。

［1］ 工程地质手册编委会．工程地质手册［S］．第三版．北京:中国建筑工业出版社，1992．

［2］ 张文彤．SPSS统计分析高级教程［M］．北京:高等教育出版社，2004．