复合材料多向层压板疲劳寿命预测①

景 钊，孙 秦

(西北工业大学航空学院，西安 710072)

0 引言

纤维增强树脂基复合材料层压板在航空航天飞行器结构中的应用越来越广泛。层压结构在工作中经常受到交变载荷作用，在交变载荷作用下，结构的疲劳损伤问题就突显出来。复合材料的脆性、损伤演变的复杂性、不同铺层间的耦合效应以及层间应力的作用，使得复合材料的疲劳问题变得复杂。因此，对复合材料疲劳的研究工作十分重要。

常用的复合材料疲劳损伤理论［1－6］有剩余强度模型、剩余刚度模型、疲劳模量模型、连续介质结合离散模型等。这些方法较突出的问题主要是在疲劳损伤参量定义、损伤演化规律构造和结构件疲劳寿命预测系统框架的合理构筑上，对不同载荷形式和铺层方式层压板的疲劳寿命预测，现有理论并不能给出一个较为普适的工程计算方法。

本文基于单向板疲劳模型理论，对3个炭纤维/树脂基T300/QY8911单向层压板的疲劳寿命进行了预测，给出了拟合表达式，在考虑多向层压板层间应力及耦合作用的情况下，给出了一套完整的疲劳寿命预测方法。同时，为了验证本文提出的疲劳寿命预测方法，对不同铺层方式的2种多向层压板在2种载荷工况下进行了疲劳试验，并对其疲劳寿命进行了预测。

1 单向层压板疲劳寿命模型

1．1 单向层压板寿命估算模型

根据Wang和Han提出的复合材料层压板的疲劳模量理论［5－9］，在等幅循环载荷作用下，把 q-lgN曲线(载荷幅值比q=σmax/σut，表征载荷的应力水平)区分为凸型和直线型，凸型形式为

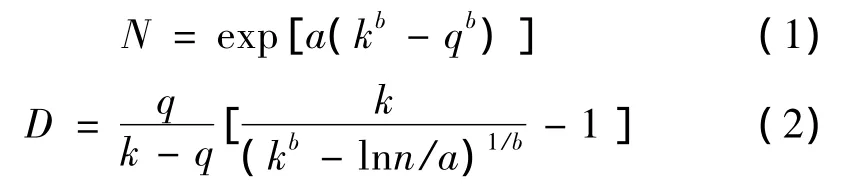
其中，a、b、k均通过试验的q-lgN曲线拟合求出，σmax和σut分别为加载方向上试件的循环最大应力和静态极限应力;D为累积应变损伤，它是循环次数n以及疲劳寿命N的函数，满足边界条件:D(0，N)=1，D(N，N)=1。若取损伤函数:D(n，N)=n/N，则这种损伤累积的概念简化成Miner线性累积损伤理论。当b=1．0时，方程(1)、(2)退化为直线型。

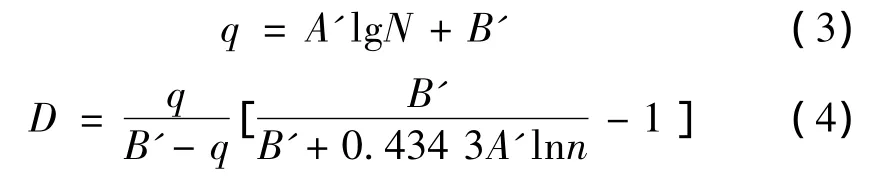
1．2 单向板在多轴循环应力作用下的疲劳损伤［10］

单向层压板在多轴循环应力作用下，当疲劳损伤累积达到一定数值后，将发生纤维失效，或基体开裂，从而导致层压板的破坏。设单向板同时有σ1、σ2和σ6主轴循环应力作用，引入等效幅值比¯q1、¯q2和¯q6:

式中 v21=E2·v12/E1，对应相应的加载载荷;Xut、Xuc分别为拉伸、压缩极限强度。

相应的累积损伤计算模型为

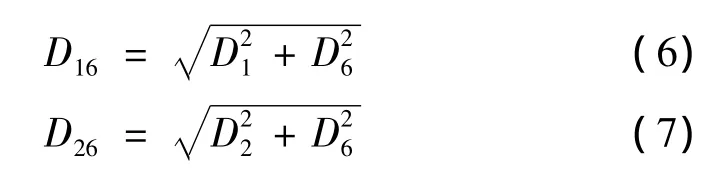
式中 D1，D2和D6分别为单向板沿纤维方向(纵向)、横向和剪切时累积损伤，由等效¯q值代入单轴应力时的损伤表达式(2)、(4)求出。

只要D16或D26中任一个首先达到1．0时，单向板就失效。当D16＞D26时，纤维失效;反之，则为基体拉压或剪切失效。

2 多向层压板疲劳寿命模型

多向层压板疲劳寿命的预测需模拟复合材料损伤累积和疲劳失效的完整过程，同时计算层压板的累积损伤和最终的疲劳寿命。多向层压板在疲劳载荷作用下，失效层的破坏原因有2种:(1)由于损伤累积发生局部疲劳破坏;(2)因为静强度不足导致局部静力破坏。这取决于外载荷是大于最先失效强度还是小于最先失效强度，应力分布每改变一次，都要计算层压板的最先失效强度，并和外载荷进行比较，确定可能发生破坏的单向层，并判断其破坏原因。

在循环应力作用下，多向层压板的总体破坏是因为每个单层逐次发生了疲劳破坏或静力破坏，其寿命用先后发生疲劳破坏的单层寿命的累积和表达。疲劳寿命分析的步骤:(1)在应力分析的基础上，判断最先失效的单层是发生局部疲劳破坏还是发生静力破坏;(2)对于发生疲劳破坏的单层，计算循环应力引起的累积损伤和疲劳寿命，对于发生静力破坏的单层，计算和静力破坏等效的疲劳累积损伤与寿命;(3)选择合适的刚度衰减准则对发生疲劳破坏或静力破坏的单层进行刚度退化;(4)返回第1步重复上述过程，直到随着单层逐次失效，最终导致层压板总体失效，用失效单层的疲劳寿命累积和表示层压板的疲劳寿命，其分析过程见图 1［11］。

图1 多向层压板的疲劳分析模型Fig．1 Analysis model of the multidirectional laminate fatigue life

2．1 多向层压板的刚度分配及层合效应

多向复合材料层压板的单轴疲劳寿命估算是在单向层压板单轴疲劳损伤估算模型基础上，通过逐一单向层板的疲劳破坏线性累加而建立的。根据刚度分配原则，计算出多向层压板中各角铺层板的单轴分配载荷。由于层压效应对层合板强度的增强作用，本文给出一个静强度增强效应系数，进而计算各角铺层板的疲劳寿命。对于多向层压板，各角铺层板的单轴载荷按载荷方向刚度分配。

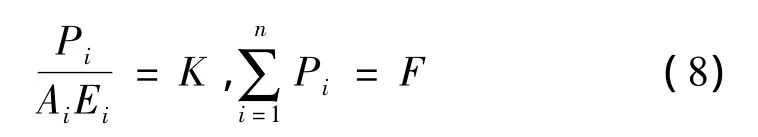
式中 n为不同铺设方向角的总数;F为层压板施加的轴向总载荷;Pi为各角铺层的轴向分配载荷;Ai为第i种角铺层截面积;Ei为第i种角铺层的加载方向刚度。

由式(8)得到各角铺层板的加载轴向载荷为

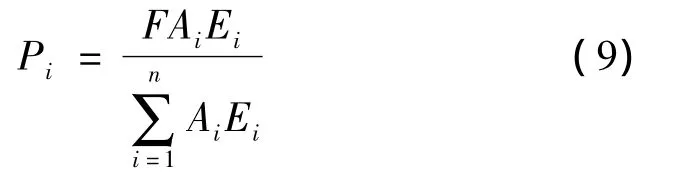
各角铺层加载方向下的偏轴刚度可由材料主轴弹性常数 E1、E2、G12及泊松比 v12得到。

根据不同类型的多向层压板静强度试验后的数据，由刚度分配折算出各单向层的静强度，用σs表示;取单向板静力试验的相应静强度数值用σu表示，两值相比:

γ为多向板的静强度增强效应系数。将增强效应系数作用于各单向板所承载的应力水平，取σmax/γ作为各单向板的疲劳寿命估算的应力水平，此静强度增强效应系数可合理反映层合效应导致的刚度增强作用。

2．2 多向层压板疲劳失效准则

当外加载荷大于某个单层最先失效强度，某个单层的纤维被立即拉断，或基体立即开裂。此时，其他单向层并没有完全破坏，需对其进行相应的刚度退化，同时应力重新分布。

本文采用的刚度衰减原则:(1)纵向纤维失效时，单向层刚度全退化为零;(2)横向纤维失效时，Q12=Q22=0，其余保留;(3)剪切失效时，Q12=Q22=Q66=0，Q11保留。单向层面内静强度破坏准则应用平面应力状态下的Tsai-Hill强度准则判定:

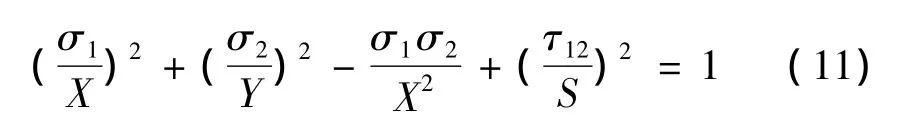
对于拉伸应力，X、Y用拉伸强度;对于压应力，X、Y用压缩强度。

2．3 多向层压板层间应力计算

纤维增强复合材料层压板自由边层间应力奇性及其引起的分层损伤，将导致复合材料层压板分层与扩展，从而引起层压板的分层疲劳破坏。本文给出一种基于力平衡关系的多向板层间应力的简化算法［12］:自由边区域层间应力分布在1～2个板厚区域内，且这一区域大部分范围内数值很小，到十分靠近自由边时，才急剧上升。因此，假设τyz与τxz的分布如图2(a)所示，σz分布如图2(b)所示。

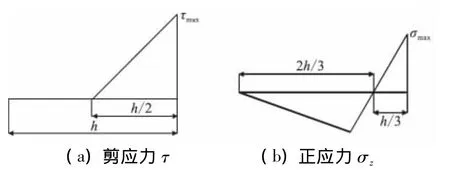
图2 剪应力和正应力分布假设Fig．2 The assumption of shear stress and normal stress

由图(2)根据力的平衡关系，可得到两不同铺向角层组间的层间奇性应力值由式(12)计算:

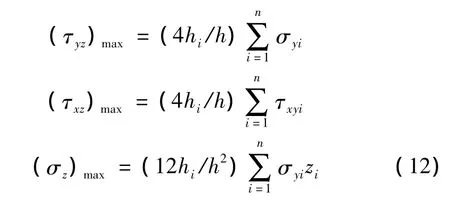
式中 hi为2不同铺向角层组间厚度较大者;h为2不同铺向角层组的总厚度;zi为第i层中面到被求层间的距离。

由式(12)获得的层间应力可能发生层间静力或疲劳破坏，层间静力破坏判据［13］为

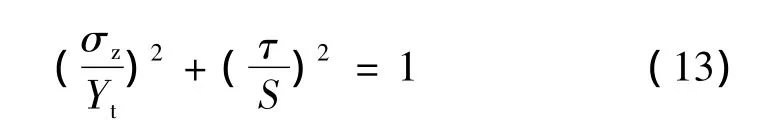
当式(13)大于1时，认为层间发生静力破坏，多向层压板的疲劳寿命则按分层后各层组的疲劳寿命累加。当式(13)小于1时，认为多向层压板疲劳过程中将发生层内疲劳破坏，且存在多向板的疲劳寿命增强效应。

2．4 多向层压板疲劳寿命估算方案

在循环载荷加载过程中，层压板因为各单层先后发生疲劳破坏或静力破坏而失效，每个发生疲劳破坏的单层存在一个疲劳寿命，用这些寿命的累积和表达层压板的疲劳寿命。本文给出了一个考虑分层效应与静强度增强效应耦合的寿命估算方案。整个多向层板疲劳寿命估算方案如图3所示。

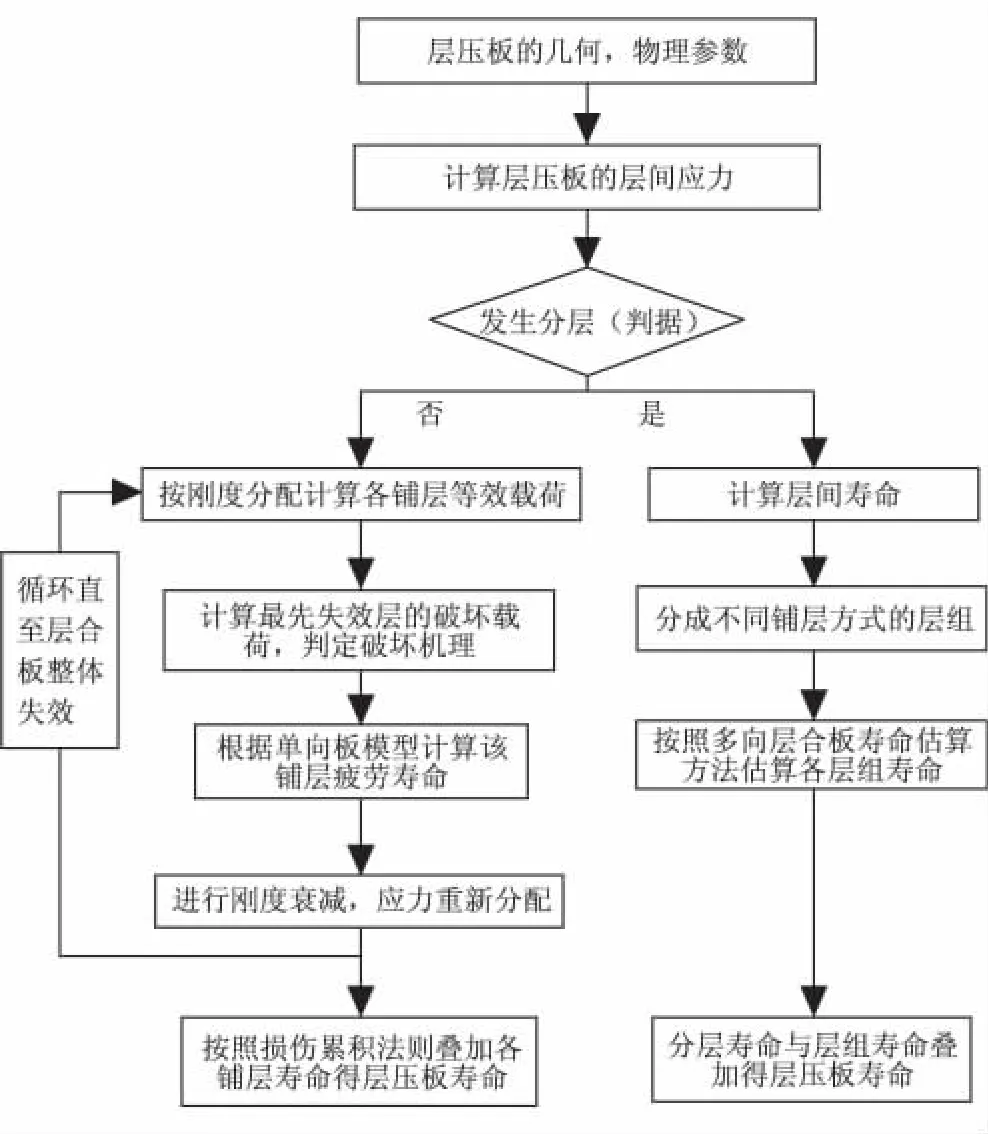
图3 层压板疲劳寿命预测框图Fig．3 Block diagram of the fatigue life prediction model for CFRP composite laminate

首先，计算层压板层间应力，判定是否发生层间破坏。如果不发生层间破坏，多向层压板的寿命估算需算出最先失效的单向层疲劳破坏寿命，按耦合效应失效模式确定刚度退化，再重新计算其他未疲劳破坏的单向层应力状态，继续计算后续最先失效状态单向层的疲劳破坏寿命。如此反复，直至多向层板因为各单向层的失效而最终整体失效。根据疲劳损伤的累积法则［14］，上述多向层压板的疲劳损伤累积过程可用估算方程描述为

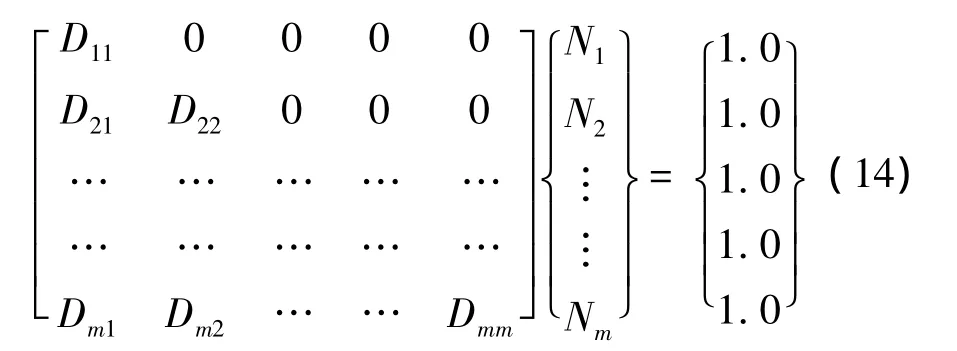
式中 Dij为层压板各角铺层的等效疲劳损伤，其中行号i从1到m代表层压板内不同角铺层单向层破坏的先后顺序;列号j从1到m表示在一个循环载荷水平内随着加载次数增大对不同角铺层单向层造成的疲劳损伤;Ni则为不同铺层角单向层的疲劳寿命。

由矩阵可看出，每一个单向层的疲劳损伤按载荷循环重分配是累加的，即每一行内部元素叠加，得到该角铺层的疲劳损伤;对角线元素叠加，即得到整个层压板在一个循环载荷内的疲劳损伤。因此，得多向层压板总的疲劳寿命为

如果判定发生层间破坏，层压板发生分层损伤进而分层。需要计算层间寿命与分层后各个层组的寿命，这里仅考虑发生一次分层的情况。层间破坏认为是胶体破坏，所以层间寿命按照单向剪切板的寿命估算公式进行估算;分层后各个层组的寿命按式(16)［12］计算:

3 实验验证

3．1 单向板疲劳模型与实验验证

首先，基于单向层压板的疲劳模量模型，对炭纤维/树脂基T300/QY8911单向层压板寿命进行了预测，复合材料单向层压板在多级应力水平下进行疲劳试验，每个应力水平下都有5个试验件。试验件构型即实验类别:［0］20纵向拉-拉疲劳试验，［90］20横向拉-拉疲劳试验，［0/90］10面内剪切疲劳试验。试验件的单向铺层厚度为0．155 mm，总厚度为3．1 mm。用最小二乘法所获得的材料拟合常数见表1。

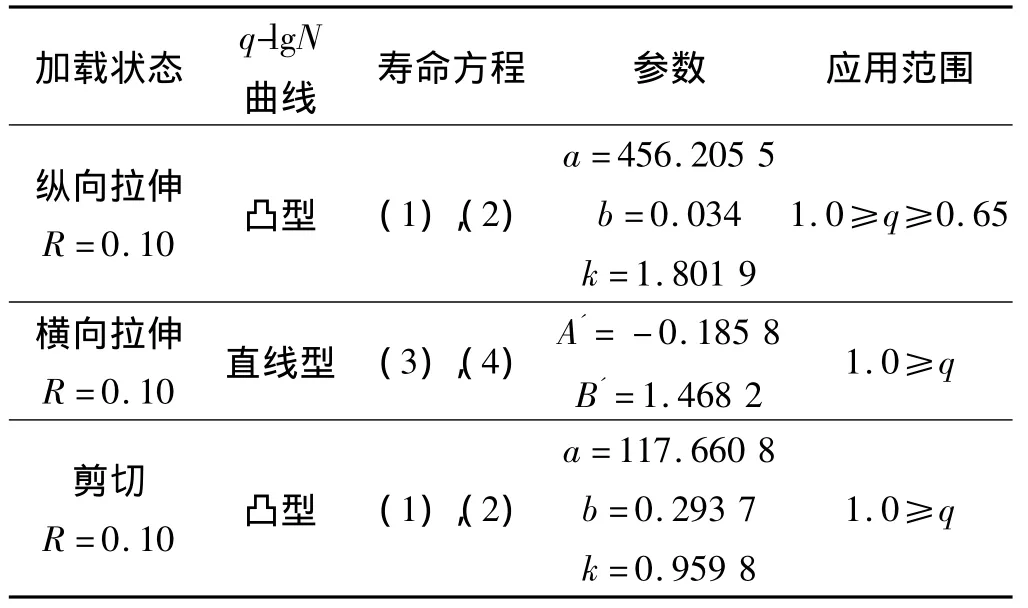
表1 单向板疲劳试验数据拟合参数(q=σmax/σult)Table 1 Fitting parameters of the unidirectional laminate with fatigue experimental data(q=σmax/σult)

3．2 多向板疲劳模型与实验验证

静力拉伸及面内剪切实验试件均夹持于MTS-810试验机的夹头中，都以2 mm/min的加载速度连续加载，直到试件破坏，连续记录载荷-应变和载荷-横梁位移数据，试件的破坏载荷及形态。静力拉伸试验与面内剪切类试验层压板试验件疲劳破坏图片如图4所示。

图4 静力拉伸和面内剪切试验件疲劳破坏Fig．4 Fatigue failure under cyclic tension load and cyclic shearing load

对2种多向层压板分别进行了纵向拉-拉和面内剪切实验，两种层压板的铺层即厚度分别为［45/0/0/0/－45/90/45/0/0/－45］S单层厚 1．55 mm，总厚度3．1 mm;［45/－45/－45/45］S单层厚0．217 mm，总厚度1．736 mm。材料主轴下的弹性模量如表2所示。

表2 单向层压板弹性模量Table 2 Elastic modulus of unidirectional laminate

根据层压效应具有增强作用，采用增强效应系数计算方法，获得的最终结果见表3。

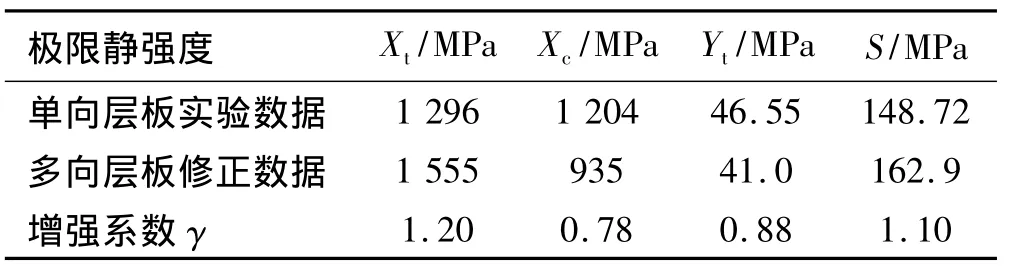
表3 单向层压板静强度修正值Table 3 Static strengths of unidirectional laminate

通过表3可看到，多向层压板由于耦合效应在纵向拉伸与剪切作用下，其强度是有所增强的，而在纵向压缩以及横向拉伸情况下，强度有所削减。

为了验证提出的预测方案，对于在不同加载方式下两种铺层方式的层压板的疲劳寿命，均按照图3的估算流程进行预测。对于铺层分别为［45/0/0/0/－45/90/45/0/0/－45］S，［45/－45/－45/45］S的层压板，测得静力拉伸破坏强度分别为 1 025．5、239．7 MPa，疲劳寿命估算及其与试验均值比较见表4、表5;面内剪切的破坏强度分别为 262．6、189．8 MPa，疲劳寿命估算及其与试验均值比较见表6、表7。表中Nexp为5个试件在该应力水平下测得的有效寿命均值，Npre为模型估算寿命。

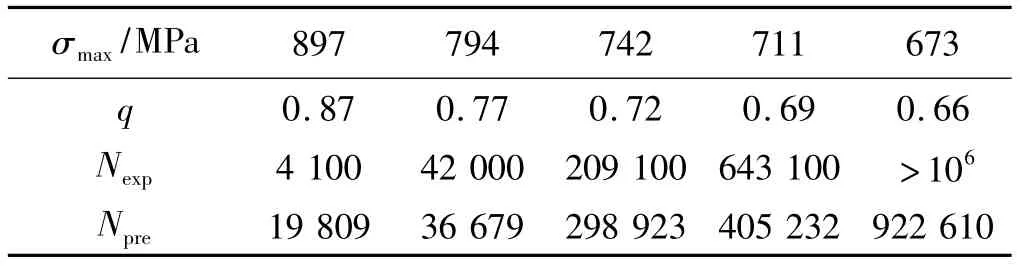
表4 层压板［45/0/0/0/－45/90/45/0/0/－45］S纵向拉伸(R=0．1)寿命估算Table 4 Life prediction of the laminate［45/0/0/0/－45/90/45/0/0/－45］S under longitudinal tension load(R=0．1)

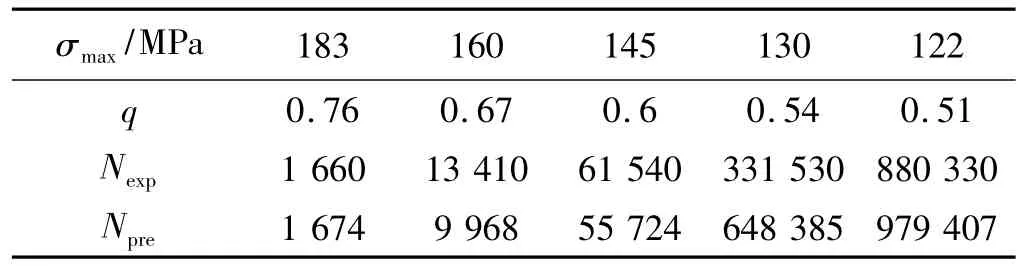
表5 层压板［45/－45/－45/45］S纵向拉伸(R=0．1)寿命估算Table 5 Life prediction of the laminate［45/－45/－45/45］S under longitudinal tension load(R=0．1)

通过以上模型预测数据与实验数据的表格对比可看出，模型有较强的预测能力，尤其是在q≤0．85这个范围内时，模型的预测误差较小，适宜在工程计算中运用。当0．85＜q＜1时，由于疲劳破坏快速发生，破坏机理复杂，且实验数据分散性较大，这是导致q在此范围内存预测寿命与实验均值有较大误差的原因。

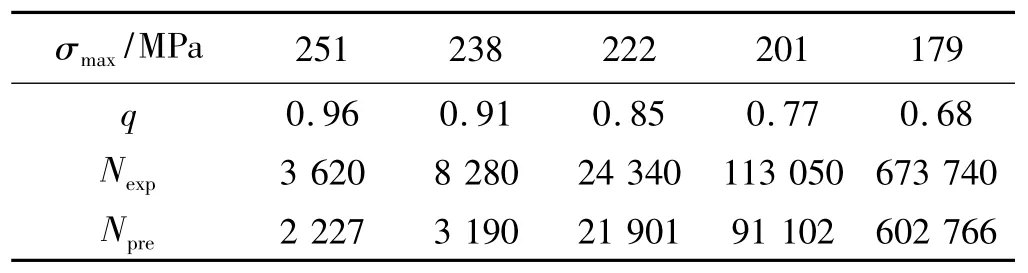
表6 层压板［45/0/0/0/－45/90/45/0/0/－45］S面内剪切(R=0．1)寿命估算Table 6 Life prediction of the laminate［45/0/0/0/－45/90/45/0/0/－45］S under shearing load(R=0．1)

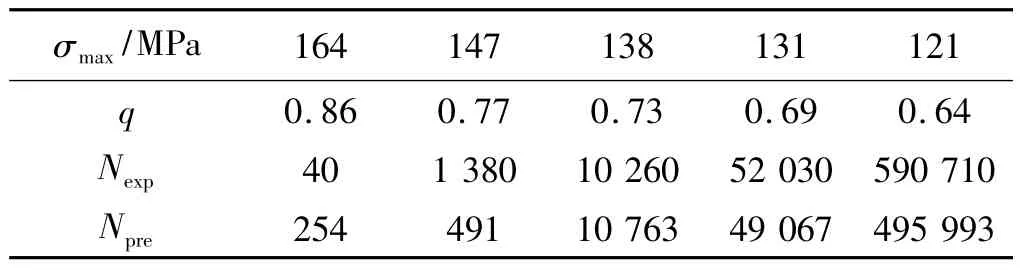
表7 层压板［45/－45/－45/45］S面内剪切(R=0．1)寿命估算Table 7 Life prediction of the laminate［45/－45/－45/45］S under shearing load(R=0．1)

4 结论

(1)提出了一种考虑层压板耦合效应的多向层压板疲劳寿命预测方法，该方法考虑了层间效应对疲劳强度的增强作用，以及层间边缘奇性导致的疲劳强度的降低。通过实验验证了模型能够很好地预测多向板层压板的疲劳寿命，适宜在工程计算中运用。

(2)层间效应对层压板的疲劳强度并不都是增强的作用，对于不同的载荷形式有所不同，仅在静力拉伸与面内剪切载荷下，疲劳强度有所增强，本文通过实验验证得出了此结论。

(3)本文的预测方法同时考虑了主受力件宏观唯象的结构变化与次受力件中由于损伤形成的各单层应力重分配的细微力学表现，且不依赖于试件铺叠方式和受载形式，建立的理论分析流程和预测方法适宜在各种工况下运用，有较广的应用前景。

［1］ 张志民，张开达，杨乃宾．复合材料结构力学［M］．北京航空航天大学出版社，1993．

［2］ Yao W X，Himmel N．A new cumulative fatigue damage model for fiber reinforced plastics［J］．Composites Science and Technology，2000，60(1):59-64．

［3］ 顾怡．FRP疲劳累积损伤理论研究进展［J］．力学进展，2001，31(2):193-202．

［4］ Han K S，Hwang W．Fatigue life prediction and failure mechanisms of composite materials［J］．Advanced Composite Materials，1992，3(1):29-52．

［5］ 韩京變，黄云峰，张金明．复合材料疲劳寿命预测［J］．复合材料学报，1987，3(4):16-24．

［6］ Han K S，Hwang W．Fatigue of composites-fatigue modulus concept and life prediction［J］．Composite Materials，1986，2(4):154-165

［7］ 顾怡，姚卫星．疲劳加载下纤维复合材料的剩余强度［J］．复合材料学报，1999，8(3):98-102．

［8］ 王丹勇，温卫东．复合材料单向层合板损伤失效研究［J］．复合材料学报，2007，10(5):142-148．

［9］ 张开达，李亚智．计及平均应力影响的疲劳寿命估算方法［C］//复合材料的现状与发展．毛天祥．NCCM211 11届全国复合材料学术会议论文集，合肥，ISBN 7231220119825PTB．4，中国科技大学出版社，2000，10:613-617．

［10］ 李亚智，张开达，张博平．一种FRP累积损伤模型及其在结构疲劳寿命估算中的应用［J］．应用力学学报，2003，3(1):54-58．

［11］ 董兴建．复合材料层压结构疲劳寿命预测方法研究［D］．西北工业大学，2002．

［12］ 诸强，杨智春，张开达．一种计及分层效应的复合材料层合板疲劳寿命计算方法［J］．西北工业大学学报，2005，12(6):708-712．

［13］ Hashin Z，Rotem A．A fatigue failue criterion for fiber reinforced materials［J］．Composite Materials，1973，7(2):448-464．

［14］ Han K S，Hwang W．Cumulative damage models and multistress fatigue life prediction［J］．Composite Materials，1986，20(2):125-153．