土体网状裂隙分形插值法生成技术

王媛 ，冯迪 ，陈尚星

(1.河海大学 岩土力学与堤坝工程教育部重点实验室，江苏 南京，210098；2.河海大学 隧道与城市轨道工程研究所，江苏 南京，210098)

由于构造运动、自然气候和人类活动等作用，自然界的土壤表面可能会发育着大量的裂隙。裂隙的存在对土体的力学性质[1−2]和渗透特性[3]产生了重要的影响，可能会导致土体的工程性质变差，裂土地区的各类工程建设常因此而遭受破坏，造成巨大的经济损失。此外，裂隙土体中水分的流动和溶质的运移在农业工程[4]和环境工程[5]中也得到广泛关注。土体裂隙网络的研究[6−9]是开展裂隙土体工作的基础，只有建立了与实际情况近似的网络，其力学和渗流分析结果才是可靠的。许多学者借鉴岩体裂隙网络的生成方法，将裂隙简化为线段，通过蒙特卡洛方法来生成土体的裂隙网络[10−11]。然而由此得到的裂隙网络与实际网络形态差别比较大，其主要原因是土体中裂隙形态与岩体中裂隙不同，这种裂隙形态的不同会引起其性质的不同，例如连通率、渗透张量以及表征单元体积等。岩体中的裂隙多为 1组(或几组)沿某优势方向的裂隙的随机分布，而土体中的裂隙多为互相联通的多边形，如果用传统的生成岩体裂隙的方法，无法模拟土体中裂隙的形态。本文作者基于分形插值理论，建立了土体裂隙网络的生成方法，并编制了可视化程序，得到了与实际裂隙网络形态较为接近的二维裂隙网络，为研究裂隙土体的力学性质和渗流特性建立了数值模型。

1 裂隙网络几何特征的调查与统计

1.1 土体裂隙网络的现场调查

采用改进的测窗法对裂隙网络进行测量与调查[12]。首先，利用数码相机进行裂隙图片的拍摄；然后对拍摄的裂隙图片进行处理，得到二元化的裂隙灰度图片，最后将处理过的裂隙图片导入AutoCAD中，对裂隙网络进行素描，得到裂隙空间分布图像，并获取裂隙网络的信息。具体步骤如下：

(1) 选择好场地以后，对拍摄区域进行选择，要求拍摄区域平整不存在凸起和凹陷，同时拍摄区域内的土体颜色要均一、少有杂色物质。在拍摄之前要对拍摄区域进行清理，去除裂隙中的充填杂物，使裂隙充分暴露出来；去除土体表面上的其他杂物，剔除它们可能对影像造成的干扰。在拍摄区域边缘放置标度尺，作为确定分析区域实际尺寸的依据和比例换算的标准。拍摄时镜头主光轴与拍摄面保持垂直，这样能够真实反映裂隙的形态，提高计算准确性。

(2) 将拍摄好的照片转储到计算机上，根据图像中的标度尺计算确定图像与实物的比例尺。剪掉图像中的标度尺部分，挑选图像质量较好并且没有干扰的区域作为计算区域，计算区域应该尽量处于照片的中央位置。将图像调整为灰度模式。对图像进行增益除噪处理，使裂隙与其他图像信息最大程度地分离。设置适当的阀值，将灰度图转换为只存在纯黑和纯白 2种颜色的二元位图，即实际裂隙网络图(如图1所示)，以此作为土体裂隙几何学特征研究的素材。

(3) 将处理过的土体裂隙图像导入到AutoCAD软件中，对照裂隙图像，用线段素描得到裂隙网络几何特征图(如图 2所示)。裂隙网络图是进行裂隙分组、统计、计算和裂隙网络几何特征分析的基础。根据图像与实物的比例尺，就可以获取裂隙几何参数的真实信息，本文中分析区域的实际尺寸(长×宽)为 275 mm×220 mm。

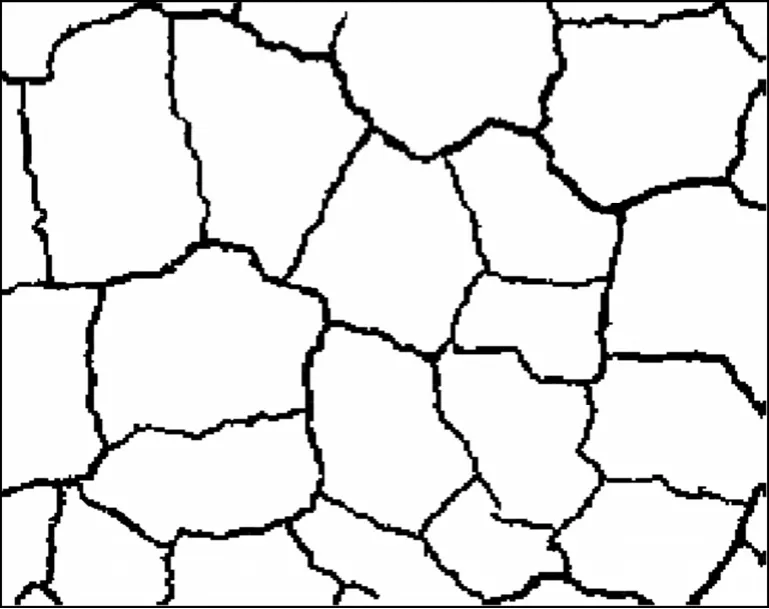
图1 实际裂隙网络图Fig.1 Graph of real crack network

图2 裂隙网络几何特征图Fig.2 Geometric features of crack network

1.2 裂隙网络的几何特征统计

通过调查发现裂隙土的裂隙大多首尾相接，最终形成由四边形、五边形、六边形及七边形组成的网状裂隙网络。为了能够在一定程度上反映裂隙的发育，需要对裂隙网络的几何特征进行概化。定义节点为裂隙与其他裂隙相交的点(如图 2中圆圈所示)，两节点间即为一条裂隙；拐点为裂隙延展方向发生明显改变的点(如图 2中三角形所示)。整个裂隙网络的几何结构由节点、拐点和裂隙段构成，可以通过以下参数来进行描述：

(1) 节点密度：单位面积的节点个数。

(2) 节点的度：节点与其他节点连接的个数，它反映了裂隙网络节点间的连接程度。如图 3所示，A点的度为1，B点的度为2，C点的度为3。

(3) 拐点密度：每条裂隙的平均拐点个数。

(4) 拐点变幅：每条裂隙拐点相对于节点连线的垂直距离(如图 4所示)，它反映了每条裂隙的细部结构形态。

图3 节点的度Fig.3 Degree of node

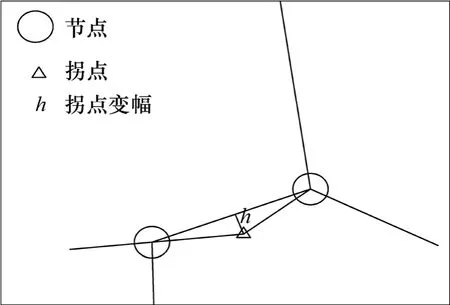
图4 拐点变幅Fig.4 Amplitude of inflection

(5) 裂隙宽度：是指裂隙张开的宽度，是描述裂隙结构特征的一个重要指标。

裂隙网络节点度的统计结果见表 1。可见：裂隙网络共有节点41个，其中36个节点的度为3。裂隙网络拐点统计结果见表 2。可见：裂隙网络共有拐点72个，裂隙共有49条，拐点个数为2的裂隙共有25条，其次为拐点个数为0和1的裂隙，分别为11条和9条。拐点的最大变幅为17.24 mm，最小变幅为0.06 mm，平均变幅为3.64 mm。裂隙宽度最大为4.12 mm，最小为1.09 mm，平均为2.57 mm。

表1 裂隙网络节点统计结果Table 1 Statistical results of crack network nodes

表2 裂隙网络拐点统计结果Table 2 Statistical results of crack network inflections

2 分形插值法生成土体的裂隙网络

裂隙土体中的网状裂隙形态复杂，裂隙延展方向及隙宽变化较大，如用直线段模拟，就会与实际形态产生较大的差别。为了更接近实际裂隙网络，需用另一种方法来进行模拟。易顺民等[13−14]在研究膨胀土裂隙时，发现裂隙面的起伏形态也具有统计意义上的自相似性符合分形特征，依据这一结果，本文建立了一种利用分形插值来生成土体裂隙网络的方法。

2.1 迭代函数系与分形插值

迭代函数系(IFS)是一种仿射映射变换方法，其实质是通过仿射映射变换，将整体的形态变换到局部，应用这一特性，人们模拟重构出了大自然中许多具有自相似形态的图案[15]。

并满足如下条件：

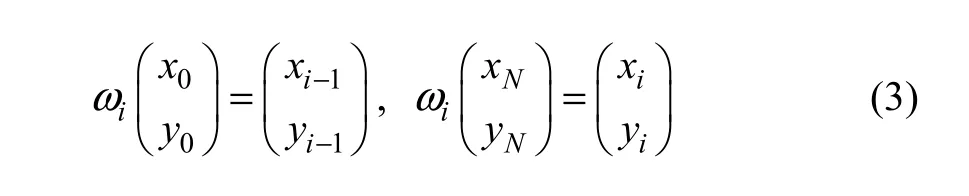
则可以确定以下方程组：

对于每个仿射变换ωi有ai，ci，di，ei，fi5 个参数，如果要确定这5个参数，就必须增加1个方程或固定其中一个参数。在这里选取参数d代表变换中垂直方向变化的参数，称其为垂直比例因子。令d为任意一个取定的实数，联解方程可得：

2.2 土体裂隙网络的生成方法

土体裂隙网络的生成中采用的参数是节点、拐点数和分维数。我们通过统计实际土体单位面积的平均节点数来生成模拟区内裂隙的节点数，然后根据节点之间位置关系生成拐点。裂隙土的裂隙符合分形特征，根据这一结论，裂隙土裂隙的形态应该具有自相似特征，我们可以根据节点、拐点的位置特征，插值出节点、拐点间的裂隙形态特征，获得的裂隙和实际裂隙具有相同的分形特征。

分形插值法生成土体裂隙网络的过程如下：

(1) 生成域和分析域。考虑到边界周围裂隙的节点可能会在域外，实际裂隙网络生成域应比分析域大一些，然后用分析区域边界去切割生成的裂隙网络，就可以得到分析域的裂隙网络图。

(2) 节点的生成。根据节点密度，计算生成域内节点数，按均匀分布随机生成节点。

(3) 确定节点间的连接关系。节点间的连接需要遵从一定的关系，即裂隙之间的拓扑关系。通过对实际裂隙网络观察发现：节点总是与周围距离相近的几个节点相连。节点的度k表示节点与其他节点的连接数，因此本文假定每个节点与其距离最近的k个节点相连，由此可以确定整个区域中所有节点间的连接关系。

(4) 拐点生成。统计节点间的拐点数，以平均值作为模拟时节点间生成的拐点数。量测每条裂隙拐点的变幅，然后对整个区域的拐点变幅值进行平均，将其作为裂隙模拟时的变幅值。设两节点的坐标分别为(x0,y0), (x1,y1)，则第i个拐点的坐标(xi,yi)为：

式中：m为拐点数；为拐点变幅平均值；α为该裂隙与x轴的夹角。

(5) 裂隙宽度。测量每条裂隙的宽度，然后对整个区域的裂隙宽度进行统计，根据下式确定第i条裂隙的宽度bi：

式中:bmax为最大隙宽；bmin为最小隙宽；random(bmax−bmin)表示在 0～(bmax−bmin)之间的均匀随机数。

(6) 分形插值。根据节点坐标和节点间的拐点坐标，由式(5)获得迭代函数的参数，通过下式进行迭代计算：

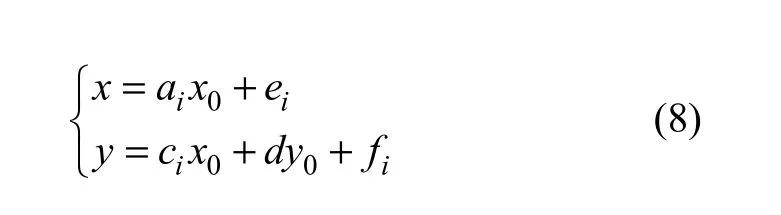
获得插值点的坐标，经过L次插值迭代后，插值点足够多便连成线，表现出裂隙的形态变化和粗细变化。

2.3 裂隙网络的生成结果与分析

2.3.1 参数的选取

裂隙网络生成域为344 mm×275 mm(长×宽)，分析域为275 mm×220 mm(长×宽)，根据实际裂隙网络几何参数的统计结果可知：相同节点密度下，生成域内节点数n为51，节点的度k平均值为3，节点间的拐点数m均值为2，拐点变幅h均值为3.64 mm，最大隙宽为4.12 mm，最小隙宽为1.09 mm，插值迭代次数L为6。改变节点坐标随机数产生种子可以得到不同的裂隙网络样本，如图5所示。

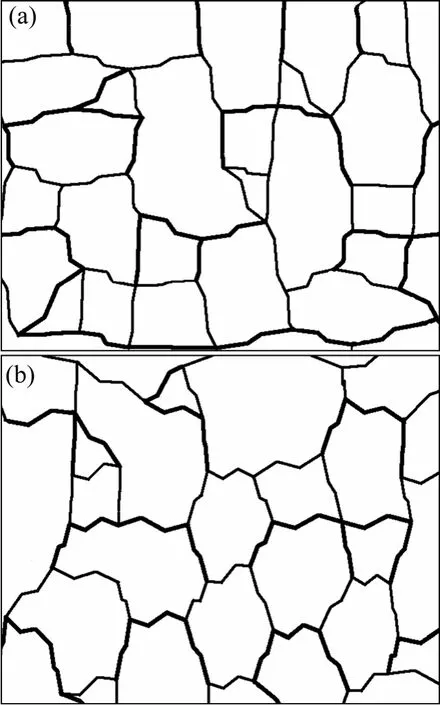
图5 不同的裂隙网络样本Fig.5 Different samples of crack network

2.3.2 节点数n的影响

生成域内节点数n对分形插值网络结果的影响如图6所示。由分维数计算方法[14]可以得到裂隙网络的维数，从图6可以看出：随着n的增大，裂隙网络的裂隙密度和分维数也在不断的增大。

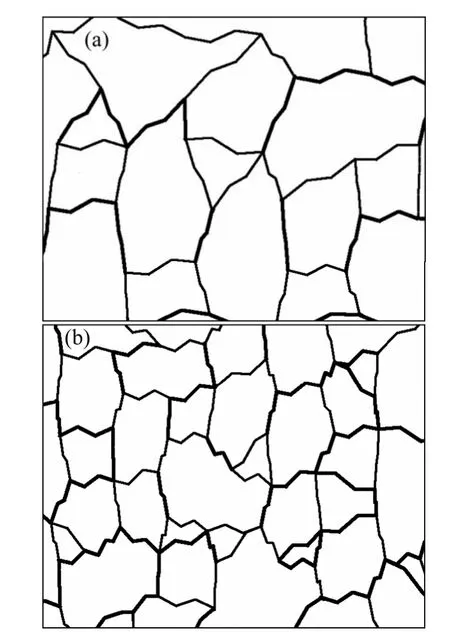
图6 参数n对分形插值网络结果的影响Fig.6 Effect of n on crack network generated by fractal interpolation

2.3.3 垂直比例因子d的影响

图7 参数d对分形插值网络结果的影响Fig.7 Effect of d on crack network generated by fractal interpolation

垂直比例因子d对分形插值网络结果的影响如图7所示，从图7可以看出：d虽然是个自由参数，但其对分形插值的结果影响很大。当d=0时，分形插值退化为线性插值，此时得到的裂隙网络不能反映土体裂隙的细部形态；随着d的不断增大，土体裂隙的细部起伏形态表现的越来越明显，裂隙网络的分维数逐渐增大；但是，当d=0.6时，裂隙已呈现出不光滑形态。因此，在裂隙网络生成过程中可以通过改变垂直比例因子d来控制土体裂隙网络的精细程度。

2.3.4 关于裂隙网络生成结果的讨论

在裂隙网络生成程序中嵌入分维数计算程序，当得到的分形插值网络,分维数等于实际裂隙网络图像的分维数时，插值结束，此时得到的分形插值网络如图8所示。

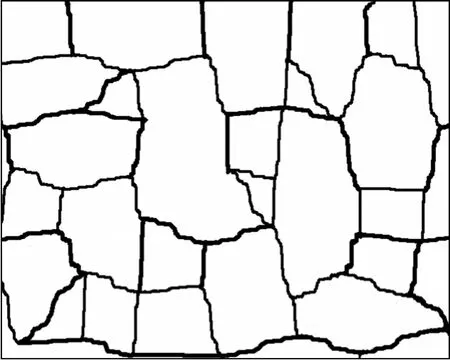
图8 分形插值网络(d=0.281，分维数1.466)Fig.8 Crack network generated by fractal interpolation

目前，土体裂隙网络的生成主要是通过蒙特卡洛方法来生成[9]，按照裂隙网络几何参数统计结果，得到裂隙网络如图9所示。该方法主要存在2个缺点：一是不能反映土体裂隙的细部起伏形态；二是与土体裂隙多为互相联通多边形的实际形态不符。将图8和图9与土体实际的裂隙网络(图1)对比可以发现：分形插值法得到的裂隙网络显然更符合实际形态。

图9 蒙特卡洛法生成的裂隙网络Fig.9 Crack network generated by Monte-Carlo method

3 土体裂隙网络的表征单元体积

由于土体中裂隙的存在，使得原来的连续介质假定变得不合理，需要用非连续介质的方法进行研究。在现阶段的研究中较为成熟并行之有效的方法是等效连续介质模型，采用等效连续介质模型可以将由于裂隙引起的力学或渗流的集中效应等效平均到整个土体中，将裂隙土体模拟为连续的土体，然后应用经典的连续介质理论进行研究分析。在应用等效连续介质进行分析时存在有效性问题，即研究对象必须存在表征单元体积(REV)[18]。表征单元体积(REV)是指当试件的体积大于某一特定值V0时，由试验获得的参数不在随试件的体积变化而变化，该体积就称为表征单元体积(如图10所示)。为此，本文引入表征单元体积的概念来对生成的裂隙网络质量做进一步地评价和讨论。

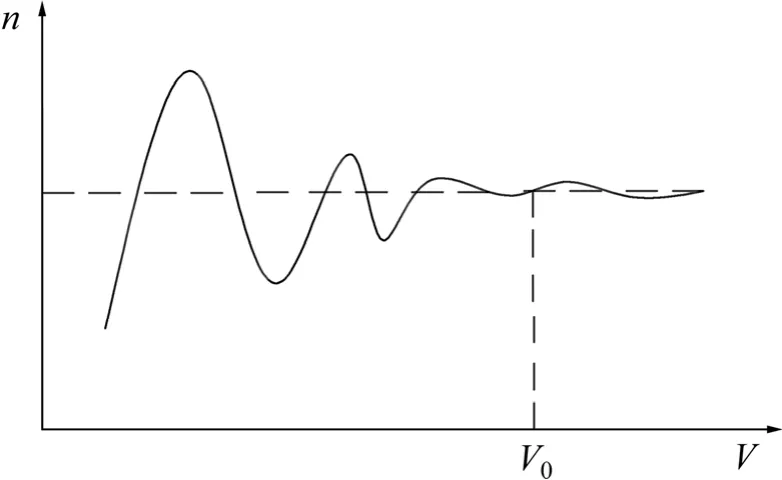
图10 表征单元体积示意图Fig.10 Schematic diagram of REV

在多孔介质中，一般根据空隙率来定义表征单元体积[19]。对于裂隙土体，其不连续性主要是由于裂隙引起的，求表征单元体积的过程就是将裂隙影响效应均一化的过程，因此可以用裂隙率来定义表征单元体积。当裂隙率不随深度变化而变化时，体裂隙率就等于面裂隙率，面裂隙率定义为：

式中：nc为面裂隙率；Ac为裂隙面积；A为裂隙土体面积。

用一系列不同尺寸的窗口(如图11所示)去切割裂隙网络，计算出每个尺寸窗口对应的裂隙率，绘制裂隙率与计算窗口面积之间的关系曲线图。当裂隙率变化连续小于误差范围且无明显变化趋势时，即认为裂隙率稳定，确定不出现大的波动的那个最小计算窗口面积，即为表征单元体积所对应的面积。

选取裂隙网络中间的220 mm×220 mm(长×宽)区域作为表征单元体积的计算区域，用步长为 13.75 mm×13.75 mm(长×宽)的16个窗口去切割裂隙网络，分形插值网络与实际裂隙网络的裂隙率随计算窗口的变化如图12所示。

图11 一系列不同尺寸的窗口Fig.11 A series of windows with different scales

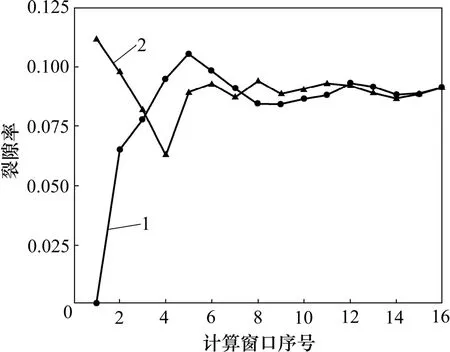
图12 裂隙率随计算窗口变化图Fig.12 Variation of crack ratio with different computing windows

从图12可以看出：实际裂隙网络的表征单元面积大约为第12个计算窗口，即165 mm×165 mm(长×宽)；模拟得到的分形插值裂隙网络的表征单元体积大约为第10个计算窗口，即137.5 mm×137.5 mm(长×宽)；从第12个计算窗口开始，两者的裂隙率趋于相同。结果表明：生成网络与实际网络的表征单元体积相差不大，两者的整体分布特征较为接近。当然，两者之间还是存在一定的误差，说明用分形插值法所得到的裂隙网络还需要进一步的优化，使其更加符合实际裂隙发育的情况。用拐点数、拐点分布特征及分维值控制生成裂隙还存在一些缺点，以后若从裂隙形态的频谱特征去统计和模拟裂隙会改善单条裂隙的相似性，同时建立裂隙间的拓扑关系函数，会使整个裂隙网络更趋于合理。

4 结论

(1) 采用改进的测窗法对裂隙网络进行调查较为简便，统计结果表明土体裂隙网络中节点的度以3居多，裂隙间的拐点个数一般为2，其次为0和1。

(2) 分形插值法生成的裂隙网络能很好地反映出土体裂隙的细部变化特征，基本符合其变化形态。裂隙网络的裂隙密度和分维数随着节点密度的增大而增大；垂直比例因子d对结果的影响很大，随着d的不断增大，土体裂隙的细部起伏形态表现得越来越明显，且裂隙网络分维数逐渐增大。

(3) 分形插值生成的裂隙网络与土体实际裂隙网络的表征单元体积和稳定裂隙率相差不大，表明两者的整体分布特征相似。

(4) 基于分形插值理论的土体裂隙网络生成技术切实可行，生成的二维裂隙网络与土体实际裂隙网络形态较为接近。不可忽略裂隙网络的随机性和裂隙深度对于土体性质的影响，如何全面考虑参数的随机性并建立土体三维裂隙网络模型需要进一步的研究。

[1] 胡卸文, 李群丰, 赵泽三, 等.裂隙性粘土的力学特性[J].岩土工程学报, 1994, 16(4): 81−88.HU Xiewen, LI Qunfeng, ZHAO Zesan, et al.Mechanical properties of fissured clay[J].Chinese Journal of Geotechnical Engineering, 1994, 16(4): 81−88.

[2] 包承钢.非饱和土的性状及膨胀土边坡稳定问题[J].岩土工程学报, 2004, 26(1): 1−15.BAO Chenggang.Behavior of unsaturated soil and stability of expansive soil slope[J].Chinese Journal of Geotechnical Engineering, 2004, 26(1): 1−15.

[3] 马佳.裂土优势流与边坡稳定分析方法[D].武汉: 中国科学院武汉岩土力学研究所, 2007: 6−9.MA Jia.Preferential flow and stability analysis method for fissure clay slopes[D].Wuhan: Institute of Rock and Soil Mechanics.The Chinese Academy of Sciences, 2007: 6−9.

[4] Tuong T P, Cabangon R J, Wopereis M C S.Quantifying flow processes during land soaking of cracked rice soils[J].Soil Science Society of America Journal, 1996, 60(3): 872−879.

[5] Alonso E E, Springman S M, Ng C W W.Monitoring large-scale tests for nuclear waste disposal[J].Geotechnical and Geological Engineering, 2008, 26(6): 817−826.

[6] Velde B.Structure of surface cracks in soil and muds[J].Geoderma, 1999, 93: 101−124.

[7] 卢再华, 陈正汉, 蒲毅彬.膨胀土干湿循环胀缩裂隙演化的CT试验研究[J].岩土力学, 2002, 23(4): 417−422.LU Zaihua, CHEN Zhenghan PU Yibin.A CT study on the crack evolution of expansive soil during drying and wetting cycles[J].Rock and Soil Mechanics, 2002, 23(4): 417−422.

[8] Bear J U, Kent T F, Anderson S H.Image analysis and fractal geometry to characterize soil desiccation cracks[J].Geoderma,2009, 154: 153−163.

[9] Li J H, Zhang L M.Geometric parameters and REV of a crack network in soil[J].Computers and Geotechnics, 2010, 37:466−475.

[10] 袁俊平.非饱和膨胀土的裂隙概化模型与边坡稳定研究[D].南京: 河海大学岩土工程研究所, 2003: 22−25.YUAN Junping.Generalized Model of Fissures Distribution &Slope Stability Analysis for Unsaturated Expansive Soils[D].Nanjing: Hohai University.Institute of Geotechnical, 2003:22−25.

[11] Li J H, Zhang L M, Wang Y.Permeability tensor and representative elementary volume of saturated cracked soil[J].Canadian Geotechnical Journal, 2009, 46(8): 928−942.

[12] 李亚萍.甘肃北山花岗岩裂隙几何特征研究[D].北京: 中国地震局地质研究所, 2005: 6−9.LI Yaping.Geometrical Characteristics of Fractures in Granite in the Beishan Area, Gansu Province[D].Beijing: China Earthquake Administration.Institute of Geology, 2005: 6−9.

[13] 易顺民, 黎志恒, 张延中.膨胀土裂隙结构的分形特征及其意义[J].岩土工程学报, 1999, 21(3): 294−298.YI Shunmin, LI Zhiheng, ZHANG Yanzhong.The fractal characteristics of fractures in expansion soil and its significance[J].Chinese Journal of Geotechnical Engineering,1999, 21(3): 294−298.

[14] 陈尚星.基于分形理论的土体裂隙网络研究[D].南京: 河海大学岩土工程研究所, 2006: 44−52.CHEN Shangxing.Reseach on crack network of soil by fractal dimension theory[D].Nanjing: Hohai University.Institute of Geotechnical, 2006: 44−52.

[15] 杨杰.分形插值及其分形维数研究[J].武汉工业学院学报,2006, 25(1): 9−11.YANG Jie.Study on fractal interpolated and its fractal dimension[J].Journal of Wuhan polytechnic University, 2006,25(1): 9−11.

[16] 王兴元, 梁庆永, 沈立新.真彩色IFS吸引子的计算机构造[J].大连理工大学学报, 2005, 45(1): 142−146.WANG Xingyuan, LIANG Qingyong, SHEN Lixin.True color IFS attractors constructed on computer[J].Journal of Dalian University of Technology, 2005, 45(1): 142−146.

[17] 陈慧琴.分形插值及分形维数的图解法[J].江西科学, 2010,28(2): 167−169.CHEN Huiqin.Study on fractal interpolation and its fractal dimension by graphic method solving[J].Jiangxi Science, 2010,28(2): 167−169.

[18] 向文飞, 周创兵.裂隙岩体表征单元体研究进展[J].岩石力学与工程学报, 2005, 24(增2): 5686−5692.XIANG Wenfei, ZHOU Chuangbing.The advances in investigation of representative elementary volume for fractures rock mass[J].Chinese Journal of Rock Mechanics and Engineering, 2005, 24(supp2): 5686−5692.

[19] Bear J.Dynamics of fluids in porous media[M].New York:Elsevier, 2007: 15−27.