基于粗糙集理论的滑坡易发性评价——以三峡库区秭归县境内为例

程温鸣 ，彭令，牛瑞卿

(1.中国地质大学(武汉) 工程学院，湖北 武汉，430074；2.三峡库区地质灾害防治工作指挥部，湖北 宜昌，443000；3.中国地质大学(武汉) 地球物理与空间信息学院，湖北 武汉，430074)

滑坡属于自然灾害中的最重要灾害类型之一，具有分布地区广、发生频率高、灾害损失严重等特点，严重威胁与危害居民生命财产安全，给国家和人民带来巨大损失。因此，科学、准确地进行滑坡灾害易发性评价，对减灾防灾具有重要意义。国内外学者利用多种方法进行过滑坡易发性评价，例如 Rotigliano等[1−4]利用地理信息系统(GIS)及空间分析进行过滑坡易发性评价与制图；Atkinson等[5−7]采用统计模型进行过滑坡易发性评价。但是，这些方法都需要地形、地质、水文和人类工程活动等多种数据，涉及到的评价指标众多，而要在这些评价指标中，科学、合理地确定模型评价指标体系是一个非常棘手的问题，也是在许多相关研究中没有解决的关键问题[8]。应用传统的分析方法及统计模型常常需要严格的数据假设条件，例如统计学中的概率分布、模糊集理论中的隶属度等，并且由于传统研究方法缺乏对滑坡系统各类复杂信息的提取和挖掘，没有充分考虑到滑坡系统行为的确定性、不确定性和线性、非线性特征，另外滑坡分析涉及到的数据信息随着获取手段和来源的极剧增多而更加复杂。因此，有必要从这些数据中提取有用的信息和知识，并将提取出来的信息和知识表示成概念、规则、规律和模式。粗糙集理论不需要预先给定任何假设条件或者先验知识，可以直接对不完整、不精确的数据进行分析处理，得到简明扼要的知识表达形式；并且它具有对数据进行信息约简的能力，能获得数据的核心知识，找出影响事件的本质因素。它为研究不精确数据的分析、推理、挖掘数据间的隐藏关系，发现潜在的知识提供了有效的工具，已被广泛应用于多个研究领域，例如遥感科学[9]、地理信息科学[10]、经济学[11]、医学[12]、工程学[13]等。但直到 2008年，Gorsevski等[14]才首次提出利用粗糙集理论进行区域滑坡研究，此后，国内外的相关研究较少。因此，本文以长江三峡库区秭归县境内为研究区，采用粗糙集理论对滑坡进行易发性评价，为三峡库区减灾防灾提供决策支持。

1 粗糙集基本原理

粗糙集(Rough sets)理论是波兰数学家Pawlak 教授于1982年提出的一种能够定量分析处理不精确、不一致、不完整信息与知识的数学工具[15]。它最初的原型来源于比较简单的信息模型，其基本思想是通过关系数据库分类归纳形成概念和规则，通过等价关系的分类以及分类对于目标的近似实现知识发现[16]。在粗糙集理论中，一个知识表达系统可定义为

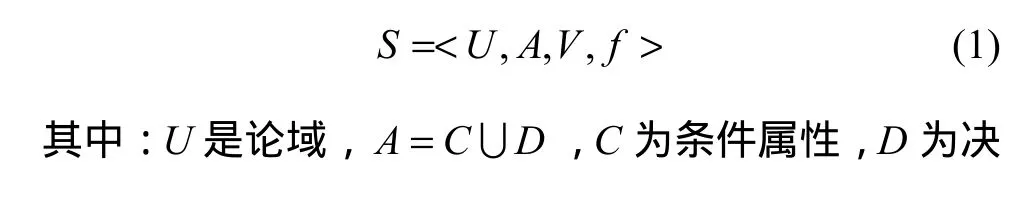
2 研究区概况及数据源

2.1 研究区概况

研究区位于长江三峡库区秭归县境内，地理坐标为 110°41′15″ ～ 110°45′00″ E，30°55′00″ ～ 30°57′30″N，图 1所示为研究区地理位置示意图。该区地处秭归盆地东部边缘，为鄂西褶皱山地，中低山侵蚀地貌。发育地层主要为侏罗系和三叠系。地层岩性主要为紫红色泥岩夹石英砂岩，灰绿色粉砂质泥岩、粉砂岩夹长石砂岩和炭质页岩，以及中厚层砂屑灰岩和泥质白云岩等。区域构造单元属于新华夏构造体系，鄂西隆起带北端和淮阳山字型构造体系的复合部位，构造格局较为复杂，主要构造行迹有黄陵背斜和秭归向斜，并发育有水田坝和张家河断裂等[18]。气候属亚热带大陆性季风型气候，具有四季分明，雨量充沛，光照充足，气候温和等特点。地质灾害有滑坡、崩塌和塌岸等，滑坡灾害占区内地质灾害总数的90%，发育的总体积达4.146×107m3。据不完全统计，区内受滑坡灾害威胁的对象包括人口约3 683人，房屋面积约1.224×105m2，预计直接经济损失达3.117×104万元。滑坡等地质灾害严重威胁人民生命财产安全，并在一定程度上制约了当地社会经济发展。

2.2 数据源

本文采用的主要数据源包括：(1) 中巴资源(CBERS)卫星数据1景(2004年4月，轨道号为04/65)，用于土地利用信息的遥感解译；(2) 1:10 000比例尺地形图，主要用于提取地形、地貌、公路和水系等相关信息；(3) 1:50 000比例尺地质图，用于提取地质和工程岩组等信息；(4) 除此之外还有该区历史滑坡存档资料和滑坡野外调查资料及部分航片等，主要用于解译历史滑坡。研究区内共解译出滑坡37处，总面积约为1.396×106m2，约占整个研究区面积的5.976%。

3 研究方法

3.1 斜坡单元划分

在过去的研究中，一般都采用网格单元进行分析计算，但是因网格单元数据资料单元小，且空间分布零碎，存在划分单元与评价因子(如坡度、坡向、斜坡结构等)之间的相关性较差的问题。故本研究以斜坡单元作为模型计算单元，进行滑坡易发性评价。斜坡单元是指侵蚀基准以上的整个斜坡系统，一个小集水区的水系两侧斜坡各被视为一个斜坡单元[19]。

本文采用“集水区重叠法”[20]，以 ArcGIS软件的Hydrology模型为工具，自动生成合适的斜坡单元，划分流程如图2所示。程序划分后需进行人工编修，建立斜坡单元编修的原则为：(1) 斜坡单元边界通常位于山脊线以及斜坡与河流谷地平坦交界处；(2) 斜坡单元不可跨越山脊及河流中心线；(3) 斜坡单元面积划分应参考滑坡和等高线等资料，依据各斜坡单元坡度坡向特征加以编修，过大或过小者，应予以切割或者合并；(4) 斜坡单元形状呈长条形，并且当坡面弯曲过大，且坡向明显变化者，应加以适当切割。

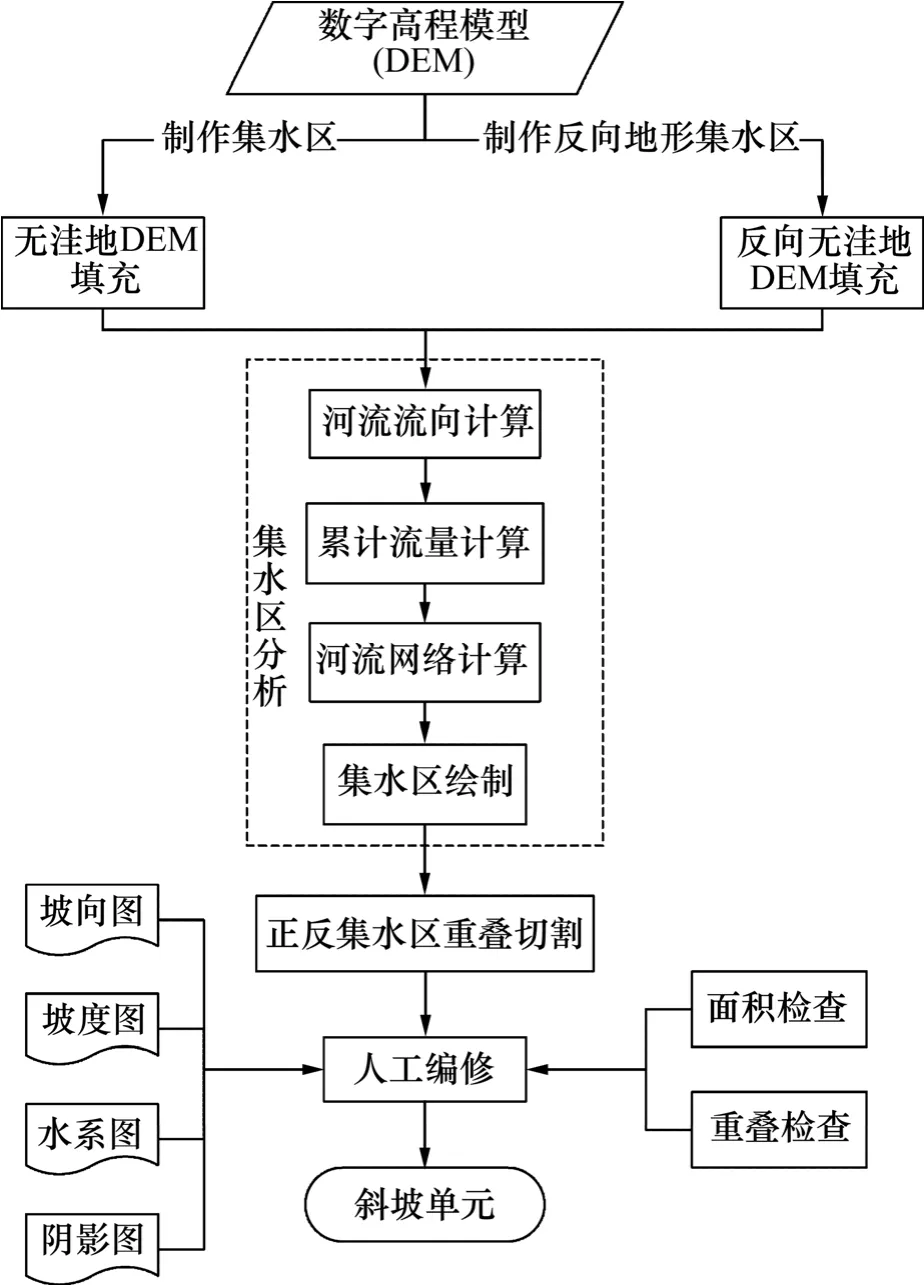
图2 斜坡单元划分流程Fig.2 Flow chart for obtaining slope unit

3.2 评价因子分析

影响滑坡灾害发生的因素包括控制因素和触发因素，前者指对滑坡发生起控制作用的地质、地貌等，该类因素在短时期内是基本稳定的，如地层岩性、地质构造、地形坡度等；后者指对滑坡发生起触发作用，这类因素作用会加速滑坡发生的时间，如人类工程活动和降雨等[21]。本文根据研究区的特点和前人研究成果，选取地形等高线、地层、斜坡结构、工程岩组、土地利用、水系缓冲距离、山谷线缓冲距离、公路缓冲距离作为一级主因子；并从主因子计算出坡度、坡向、平面曲率、剖面曲率、地形起伏度二级因子；同时，通过统计计算各斜坡单元内的主坡向、主坡度，平均坡度、平均高程、平均山谷线缓冲距离、平均水系缓冲距离、平均公路缓冲距离，最大坡度、最大高程以及坡度、高程、平面曲率、剖面曲率的标准差作为三级因子，共20个参数作为模型的初始评价因子，部分评价因子如图3所示。

3.3 基于粗糙集的滑坡易发性评价

由 20个初始评价因子对应的条件属性和滑坡对应的决策属性(1代表滑坡或者易发，0代表非滑坡或者不易发)构成最初决策表，在 RSES2软件系统中首先对连续型属性因子进行离散化，然后对最初决策表进行约简，通过去掉冗余条件属性，得到决策表的最小条件属性集和核。以约简后的斜坡结构、工程岩组、地层、主坡向、主坡度、坡度标准差、平均坡度、平均高程、平均公路缓冲距离、平均水系缓冲距离、地形平面曲率和地形剖面曲率 12个属性构成的核为最终条件属性，并与决策属性构成约简后的决策表。

随机选择约简后决策表内80%的滑坡和32%的非滑坡作为规则提取数据，构成规则提取决策表，以20%的滑坡作为检验数据，其中规则提取决策表包括 28个滑坡单元和100个非滑坡单元。利用穷举算法对规则提取决策表进行规则提取，得到知识规则集合。利用知识规则集合对约简后的决策表分类，得到整个研究区的决策属性值，把决策属性值导入到 ArcGIS中生成滑坡易发性图。最后利用检验数据对粗糙集方法的预测结果进行验证，并与其他模型方法预测结果进行对比。

4 结果与分析

对规则提取决策表共提取出1 445条决策规则，其中决策属性为易发性的规则有692条，决策属性为不易发性的规则有753条，每条决策规则代表在决策表中发现的分类模式。在所有决策规则中随机选取20条规则如表1所示，例如对于决策属性为易发性的第一条规则表示滑坡易发生在斜坡结构为顺向坡、工程岩组为软硬相间类型、坡向为西北向、坡度标准差大，即斜坡单元内坡度变化大或者地形粗糙，地形剖面曲率较大，即地形为容易汇水形成滑动面的凹地形区域。这说明研究区内滑坡主要受斜坡结构、地层岩性和地形地貌的影响；对于决策属性为不易发的第一条规则表示滑坡不易发生在斜坡结构为逆向坡、地层为嘉陵江组第三段和地形坡度变化极小的区域，由于嘉陵江组第三段以白云岩、灰岩为主，硬度大、难风化，地形坡度变化小即地形地貌较稳定。这也说明研究区内滑坡的发生主要受内部因素控制，即如果不存在发生滑坡的地质及地形地貌条件，即使有外部因素的影响，也较难以形成滑坡。

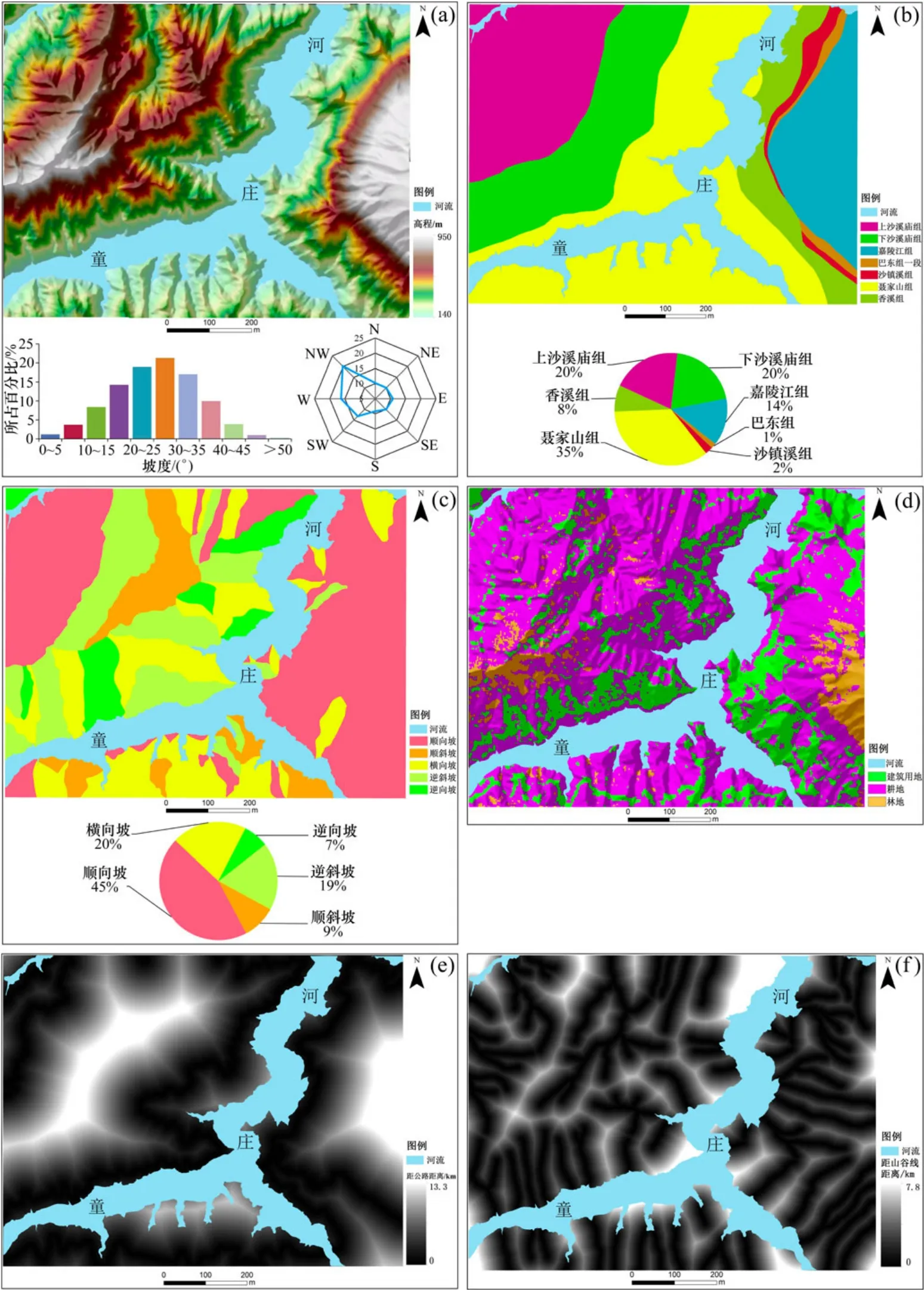
图3 评价因子Fig.3 Evaluation factors data

上面提取的决策规则“强度”为1～44，规则“强度”是指决策表中满足某条规则的对象个数，例如某规则“强度”为10，即表示在规则提取决策表中有10个斜坡单元满足该条规则。通过设置不同“强度”得到不同的规则集合，从而利用不同规则集合对决策表进行分类，可得到不同的分类结果。图4所示为“强度”从1到4的评价结果。随着“强度”的增大，检验数据的分类精度有所下降(表2)。当“强度”大于3时，出现了分类结果不确定的斜坡单元(图 4(d))，即根据当前规则集合，部分斜坡单元无法准确确定其所属类别。确定单元占全部单元的比例为“覆盖度”(Coverage)，其值为 1时表示决策表中不存在不确定性，即提取的知识规则能对决策表进行精确分类，图4中不同规则“强度”下的“覆盖度”见表2所示。

表 1 决策规则Table 1 Deterministic rules for landslide susceptibility

选择 Logistic模型和 K 最近邻(K-Nearest neighbor，简称KNN)法的预测结果与粗糙集方法预测结果进行对比，其中Logistic模型(概率分割点为0.5)[22]和KNN算法的预测结果如图4(e)和图4(f)所示。本文采用正确预测比率Ri作为模型方法预测能力评价指标，Ai表示第i种模型方法预测结果中易发区所占整个研究区面积的比例，Li表示第i种模型方法预测结果中预测正确的滑坡所占全部滑坡的比例，即Ri=Li/Ai，其中Ri越大，表示模型方法的预测能力越强。例如粗糙集方法预测到整个研究区面积的 21.7%为易发区，该区中包含已发生滑坡的 97.7%，所以该方法的Ri为4.5，而Logistic模型和KNN算法的Ri分别为2.5和3.8(见表3)。因此，在本研究区内粗糙集方法的预测能力优于Logistic模型和KNN算法。

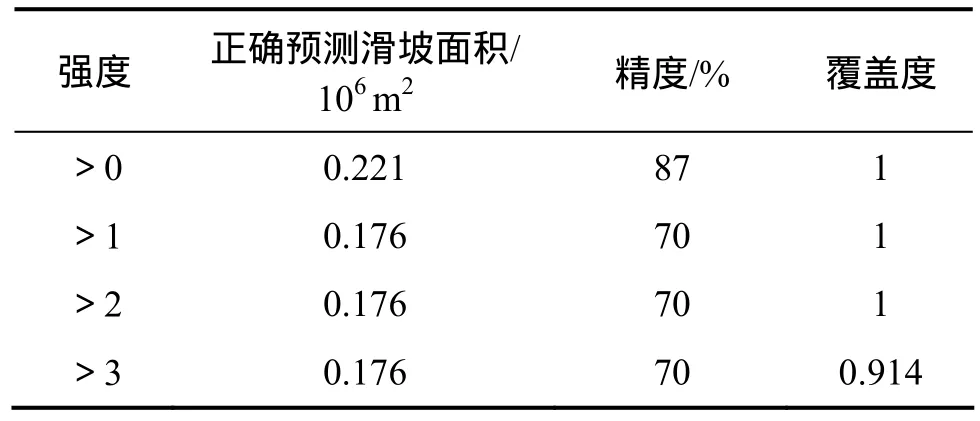
表2 不同规则“强度”下滑坡检验数据的预测精度Table 2 Accuracy of model based on different strengths of rules

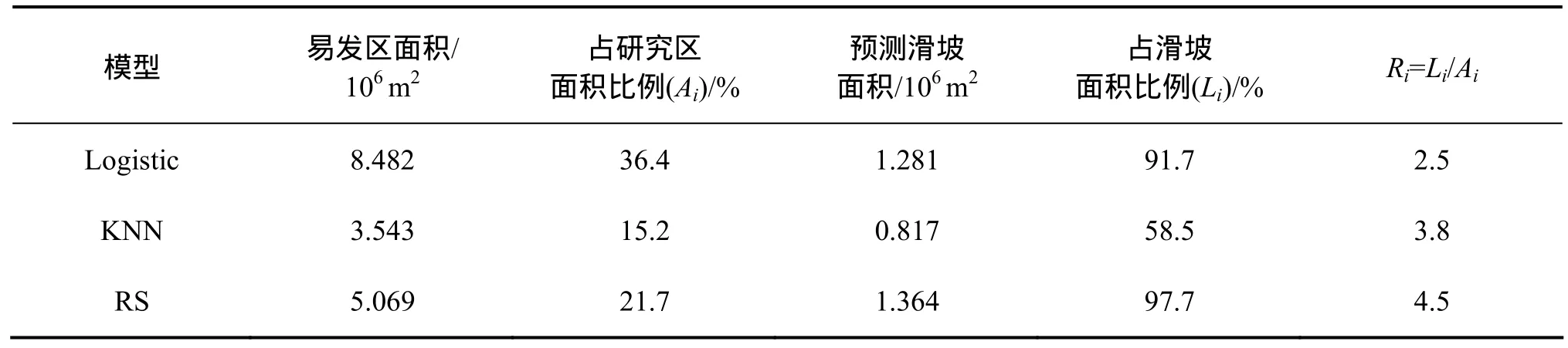
表3 不同模型方法预测结果对比Table 3 Comparison of results based on different models

图4 基于不同模型方法的滑坡易发性评价结果Fig.4 Landslide susceptibility maps based on different models

5 结论

(1) 利用粗糙集理论对滑坡易发性评价因子进行属性约简，识别出引起滑坡灾害的关键及核心影响因素。通过对核心评价因子和滑坡数据进行知识规则提取，进而对其推理、挖掘数据间的隐藏关系，最终得到以斜坡单元为基础的滑坡易发性图，其中易发区面积占研究区总面积的 21.7%，主要分布在斜坡结构为顺向坡，地层岩性为软岩、软硬相间岩，以及靠近水系及公路开挖的区域。

(2) 通过滑坡检验数据分析计算，粗糙集方法的预测精度为87%，与Logistic模型和KNN算法的预测结果相比，粗糙集方法的预测能力最优。表明粗糙集出色的数据分析能力对寻找区域滑坡灾害发生的内在规律完全有效，它是一种行之有效的滑坡易发性评价方法，并具有极大的应用潜力。

[1] Conoscenti C, Maggio C D, Rotigliano E.GIS analysis to assess landslide susceptibility in a fluvial basin of NW Sicily (Italy)[J].Geomorphology, 2008, 94(3/4): 325−339.

[2] Sarkar S, Kanungo D P, Patra A K, et al.GIS based spatial data analysis for landslide susceptibility mapping[J].Journal of Mountain Science, 2008, 5(1): 52−62.

[3] Jiménez-Perálvarez J D, Irigaray C, Hamdouni R El, et al.Building models for automatic landslide susceptibility analysis,mapping and validation in ArcGIS[J].Natural Hazards, 2009,50(3): 571−590.

[4] 石菊松, 石玲, 吴树仁.利用 GIS 技术开展滑坡制图的技术方法与流程[J].地质通报, 2008, 27(11): 1810−1821.SHI Jusong, SHI Ling, WU Shuren.Techniques and procedures of applications of the GIS technique in landslide map making[J].Geological Bulletin of China, 2008, 27(11):1810−1821.

[5] Atkinson P M, Massari R.Autologistic modeling of susceptibility to landsliding in the Central Apennines, Italy[J].Geomorphology, 2011, 130(1/2): 55−64.

[6] Nandi A, Shakoor A.A GIS-based landslide susceptibility evaluation using bivariate and multivariate statistical analyses[J].Engineering Geology, 2010, 110(1/2): 11−20.

[7] 王卫东, 陈燕平, 钟晟.应用CF和Logistic回归模型编制滑坡危险性区划图[J].中南大学学报: 自然科学版, 2009, 40(4):1127−1133.WANG Weidong, CHEN Yanping, ZHONG Sheng.Landslides susceptibility mapped with CF and Logistic regression model[J].Journal of Central South University: Science and Technology,2009, 40(4): 1127−1133.

[8] 汪华斌, 吴树仁, 汪微波.滑坡灾害空间智能预测展望[J].地质科技情报, 2008, 27(2): 17−20.WANG Huabin, WU Shuren, WANG Weibo.A framework for intelligent prediction of landslide hazards[J].Geological Science and Technology Information, 2008, 27(2): 17−20.

[9] Lei T C, Wan S, Chou T Y.The comparison of PCA and discrete rough set for feature extraction of remote sensing image classification: A case study on rice classification, Taiwan[J].Computational Geosciences, 2008, 12(1): 1−14.

[10] Leung Y, Fung T, Mi J S, et al.A rough set approach to the discovery of classification rules in spatial data[J].International Journal of Geographical Information Science, 2007, 21(9):1033−1038.

[11] Cheng C H, Chen T L, Wei L Y.A hybrid model based on rough sets theory and genetic algorithms for stock price forecasting[J].Information Sciences, 2010, 180(9): 1610−1629.

[12] Ningler M, Stockmanns G, Schneider G, et al.Adapted variable precision rough set approach for EEG analysis[J].Arti fi cial Intelligence in Medicine, 2009, 47(3): 239−261.

[13] Huang R Y, Mao I S, Lee H K.Exploring the deterioration factors of RC bridge decks: A rough set approach[J].Computer-Aided Civil and Infrastructure Engineering, 2010,25(7): 517−529.

[14] Gorsevski P V, Jankowski P.Discerning landslide susceptibility using rough sets[J].Computers, Environment and Urban Systems, 2008, 32(1): 53−65.

[15] Pawlak Z.Rough set[J].International Journal of Computer and Information Sciences, 1982, 11(5): 341−356.

[16] 王国胤, 姚一豫, 于洪.粗糙集理论与应用研究综述[J].计算机学报, 2009, 32(7): 1229−1246.WANG Guoyin, YAO Yiyu, YU Hong.A survey on rough set theory and applications[J].Chinese Journal of Computers, 2009,32(7): 1229−1246.

[17] 张文修, 吴伟志.粗糙集理论介绍和研究综述[J].模糊系统与数学, 2000, 14(4): 1−12.ZHANG Wenxiu, WU Weizhi.An introduction and a survey for the studies of rough set theory[J].Fuzzy Systems and Mathematics, 2000, 14(4): 1−12.

[18] 胡立山, 冷坚, 王锡璠, 等.1:5万新滩(西)、过河口(西)幅区域地质调查报告[R].武汉: 湖北省地质矿产局, 1995: 1−3.HU Lishan, LENG Jian, WANG Xifan, et al.1:50 000 of Xintan(west), Guo Hekou(west) site area geological survey reported[R].Wuhan: Bureau of Geological Exploration and Development of Hubei Province, 1995: 1−3.

[19] Guzzetti F, Carrara A, Cardinali M, et al.Landslide hazard evaluation: a review of current techniques and their application in a multi-scale study, Central Italy[J].Geomorphology, 1999,31(1/2/3/4): 181−216.

[20] Xie M W, Esaki T, Zhou G Y.GIS-based probabilistic mapping of landslide hazard using a three-dimensional deterministic model[J].Natural Hazards, 2004, 33(2): 265−282.

[21] 殷坤龙.滑坡灾害预测预报[M].武汉: 中国地质大学出版社,2004: 24−26.YIN Kunlong.Landslide hazard prediction and evaluation[M].Wuhan: China University of Geosciences Press, 2004: 24−26.

[22] 彭令, 牛瑞卿, 陈丽霞.GIS支持下三峡库区秭归县滑坡灾害空间预测[J].地理研究, 2010, 29(10): 1889−1898.PENG Ling, NIU Ruiqing, CHEN Lixia.Landslide hazard spatial prediction in Zigui county of the Three Gorges Reservoir area based on GIS[J].Geographical Research, 2010, 29(10):1889−1898.