为何弱阻尼振动的振幅呈指数规律衰减

郑金

(凌源市职教中心 辽宁 朝阳 122500)

机械振动包括简谐运动、阻尼振动和受迫振动，其中不受驱动力的阻尼振动为自由振动，反之为受迫振动.对于阻尼振动，若阻力大小恒定，则称为恒阻尼振动；若阻力大小跟速度成正比，则称为线性阻尼振动. 对于线性自由阻尼振动，按阻力大小，依次分为过阻尼状态、临界阻尼状态和弱阻尼状态三种情形，其中只有弱阻尼振动具有周期性，振幅按指数规律衰减，条件是阻力很小.机械线性力主要为介质阻力，如空气阻力，液体的粘滞阻力等.条件是物体运动速度较小，否则就不是线性力了.例如,弹簧振子在液体中的振动，若粘滞阻力与运动速度成正比，则为线性自由阻尼振动，当阻力非常小时，为弱阻尼振动.

无论机械阻尼振动，还是电磁阻尼振动或振荡，只要阻尼是线性的，就遵循相同的规律，即物理量的变化满足二阶常系数齐次线性微分方程x″+px′+qx=0，其通解由特征方程r2+pr+q=0的两个根r来确定.那么,如何推导振动的微分方程和通解呢？为何弱阻尼振动振幅按指数规律衰减？时间常数与瞬态过程的时间常数和谐振电路的固有周期之间有何关系？下面以两种电磁线性阻尼振动为例进行分析.

1 安培力阻尼振动

【例1】如图1所示，固定的水平光滑金属导轨，间距为l，左端接有阻值为R的电阻，处在方向竖直向下、磁感应强度为B的匀强磁场中，质量为m的导体棒与固定弹簧相连，放在导轨上，导轨与导体棒的电阻均可忽略．初始时刻，弹簧恰处于自然长度，导体棒具有水平向右的初速度v0．在沿导轨往复运动的过程中，导体棒始终与导轨垂直并保持良好接触．试分析在弱阻尼状态下导体棒的运动规律.

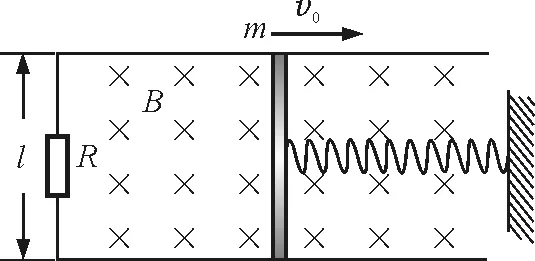
图1

解析：导体棒切割磁感线而产生的感应电动势为E=Blv，则受到的安培力大小为

开始时,导体棒受到的弹簧弹力和安培力都为阻力，由牛顿第二定律有

即

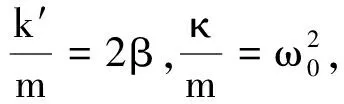
(1)

式中ω0为无阻尼时弹簧振子的固有角频率，β为阻尼因数.

二阶微分方程即x″+px′+qx=0的解与指数函数密切相关，原因是对于指数函数x=ert，当r为常数时，与它的各阶导数只相差一个常数因子.因此,只要取适当的常数r，就能使x=ert满足微分方程.为了确定常数r，可将x=ert,x′=rert和x″=r2ert代入微分方程，得到特征方程为

r2+pr+q=0

由此可知方程(1)的特征方程为

其两个根为

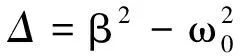
对于弱阻尼运动状态，即当β<ω0时，特征方程的两个根为

此时微分方程的两个解为x1=er1t=eat·eibt和x2=er2t=eat·e-ibt，为了得到实函数形式，可利用欧拉公式eiθ=cosθ+isinθ将其化为三角函数形式，是一对共轭复数.实部为

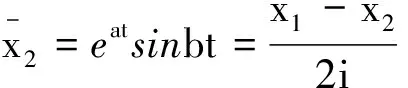
都等于两个特解的线性叠加，则由解的叠加原理可知，它们也是微分方程的解，且二者比值cotbt不是常数，即线性无关，所以通解为

由辅助角公式可知其等价式为x=Aeat(sinbt+φ).

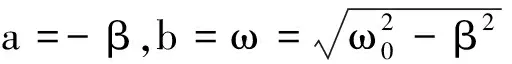
x=Ae-βtsin(ωt+φ)

(2)

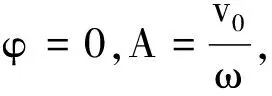
振幅衰减的时间常数为

(3)

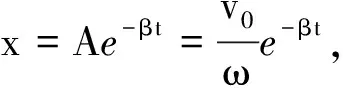
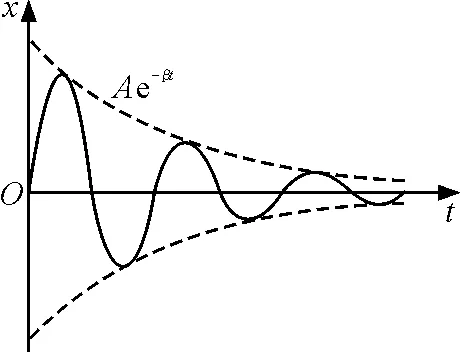
图2

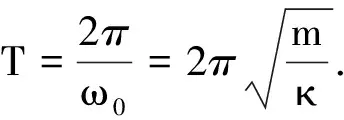
2 RLC串联电路阻尼振荡

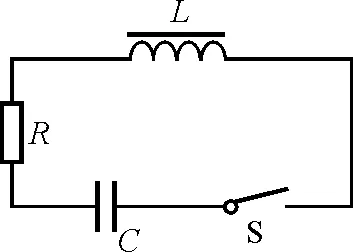
图3

【例2】如图3所示，有一个电阻R,自感L,电容C和电源E串联组成的电路，其中R,L及C为常数，电容器已充电，当闭合开关S时，试推导电容器两极电压随时间变化的微分方程及在弱阻尼状态下电压随时间变化的规律.

解析：当开关S接通后，电路中的电流由无到有，突然增大，使电感线圈产生的磁场增强，即磁感应强度B增大，则穿过线圈的磁通量Φ=BS增大，因此,线圈产生自感电动势大小为

电容器开始带电量为qm，当放电量为q时，电容器剩余电量为

Q=qm-q=CuC

因此两极板间的电压为

则放电电流为

由基尔霍夫电压定律列出回路电压方程为

uC-EL-Ri=0

可得

即

令

可得RLC串联电路的自由阻尼振荡的微分方程为

(4)

若推导电容器所带电荷量Q的变化规律，则由回路电压方程

及放电电流

得自由阻尼振荡方程为

在β<ω0的条件下，为弱阻尼振荡状态.对方程(4)由二阶常系数齐次线性微分方程的通解公式得

uC=Ae-βtsin(ωt+φ)

(5)

取导数并利用初始条件

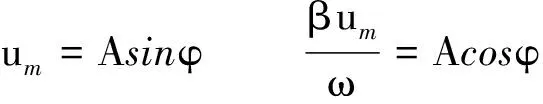
得

所以，当无源RLC串联电路处于弱阻尼振荡状态时，振幅按e-βt的指数规律衰减，时间常数为

(6)

RLC串联电路放电过程的uC-t图像如图4所示，可见阻尼振荡具有周期性，角频率为

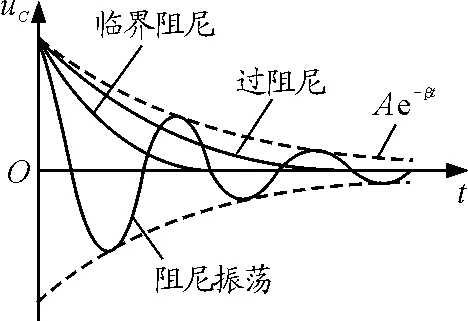
图4

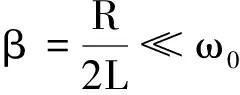
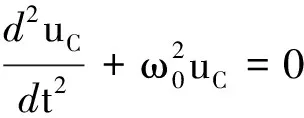
这是无阻尼时LC串联电路的自由振荡方程.角频率为

固有周期为

假如将电路中的周期性储能元件电容器去掉，换为直流电源，当闭合开关S时，对RL串联电路的充电过程为瞬态过程，回路电压方程为

即为

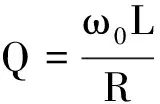
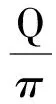
也可从能量损耗的角度来理解Q的含义，如图4所示，对于弱阻尼振荡，电容器两端电压振幅的包络线方程为uCm=Ae-βt，每个振幅对应的能量为

则相邻两个振幅对应的能量差为

而t2=t1+T，可知

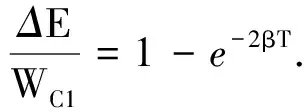
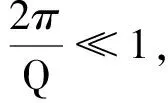
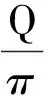
参考文献

1 同济大学数学教研室.高等数学(下册).北京：高等教育出版社，1986.352～360

2 漆安慎，杜婵英.力学基础.北京：高等教育出版社，1987.427～429

3 赵凯华，陈熙谋.电磁学(下册).北京：高等教育出版社，1988.522，730～732

4 杨晓雷.串联谐振电路Q值的计算与意义.物理通报，2011(10)：15

5 赵健生,等.阻尼振动系统普遍性质的研究.物理通报，2000(5)：5