对一道高考题的理论分析

谢丽

(咸阳师范学院 陕西 咸阳 712000)

【题目】如图1(a)，在x>0的空间中存在沿y轴负方向的匀强电场和垂直于xOy平面向里的匀强磁场，电场强度大小为E，磁感应强度大小为B.一质量为m，带电荷量为q(q>0)的粒子从坐标原点O处，以初速度v0沿x轴正方向射入，粒子的运动轨迹见图1(a)，不计粒子的重力.

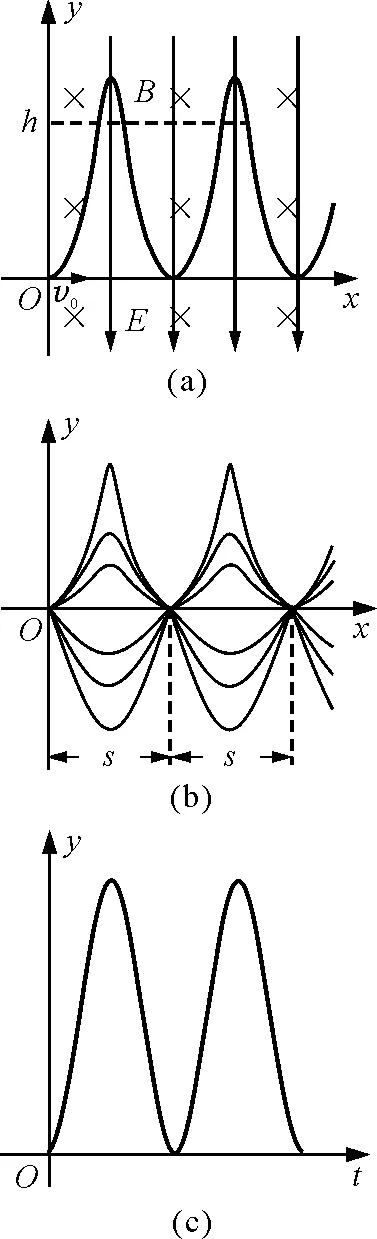
图1

(1)求该粒子运动到y=h时的速度大小v；

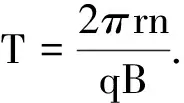
Ⅰ．求粒子在一个周期T内，沿x轴方向前进的距离s；

Ⅱ．当入射粒子的初速度大小为v0时，其y-t图像如图1(c)所示，求该粒子在y轴方向上做简谐运动的振幅A，并写出y-t的函数表达式.

该题没有按照电磁场常规的考法考查学生，带电粒子既不是只在磁场中做匀速圆周运动，也不是只在电场中做类平抛运动，而是两种运动的“合成”.因此,粒子的运动规律不是高中知识水平可以求解的.现在首先给出常规解法，然后，利用高等数学的基本知识，结合牛顿第二定律，从理论上分析粒子的运动规律，在此基础上给出第二问的两个结果.

常规解法：

(1)由于洛伦兹力不做功，只有电场力做功，由动能定理有

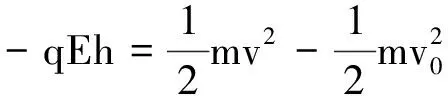
(1)

由式(1)解得

(2)

(2)Ⅰ.由图1(b)可知，所有粒子在一个周期T内沿x轴方向前进的距离相同，都等于恰好沿x轴方向匀速运动的粒子在T时间内前进的距离.设粒子恰好沿x轴方向匀速运动的速度大小为v1，则

qv1B=qE

(3)

又

s=v1T

式中

Ⅱ．设粒子在y轴方向的最大位移为ym,即图1(c)曲线的最高点处，对应的粒子运动速度大小为v2(方向沿x轴)，因为粒子在y方向上的运动为简谐运动，因而,在y=0和y=ym处粒子所受的合外力大小相等，方向相反，则

qv0B-qE=-(qv2B-qE)

(4)

由动能定理有

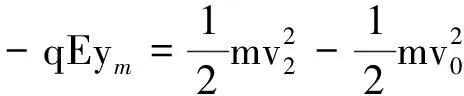
(5)

又

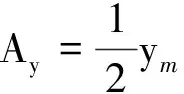
(6)

由式(4)～(6)解得

可写出图1(c)曲线满足的简谐运动y-t函数表达式为

理论分析：

考察在任一时刻t，设粒子的速度大小为v，速度与水平方向的夹角为θ，粒子沿水平方向的速度为vx，沿竖直方向的速度为vy.如图2所示，则有

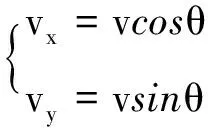
(7)

粒子受到洛伦兹力与电场力的作用，其受力如图3所示.

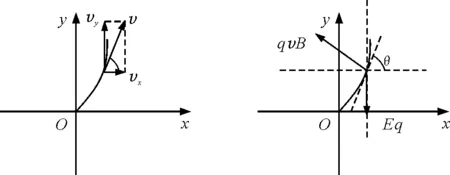
图2 粒子的速度分解示意图 图3 粒子的受力分析示意图

把粒子受到的外力在水平方向和竖直方向进行正交分解.根据牛顿第二定律，在水平方向

max=-qvBsinθ

在竖直方向

may=qvBcosθ-Eq

(8)

其中ax，ay分别为粒子在水平和竖直方向的加速度，加速度与速度的关系为

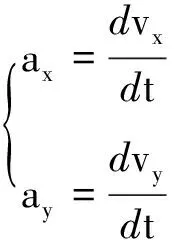
(9)

根据式(7)～(9)可以得到关于vx，vy的一组常微分方程组

(10)

(11)

初始条件为

vx|t=0=v0vy|t=0=0

将方程组中的式(11)进行微分，并将式(10)带入可得到关于vy的二阶常微分方程

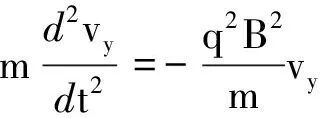
(12)

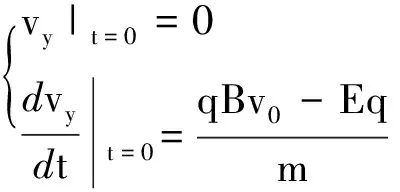
(13)

根据式(12)、(13)可以解得

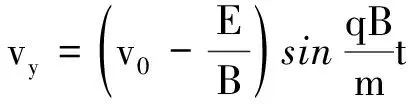
(14)

将式(14)带入式(10)可以计算得到

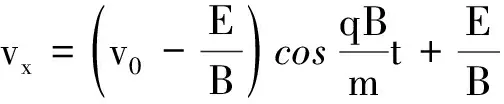
(15)

计算出vx，vy的表达式后，在区间[0,t]上进行积分便可以得到x,y关于时间t的表达式

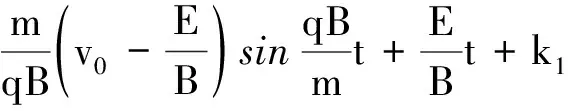
(16)

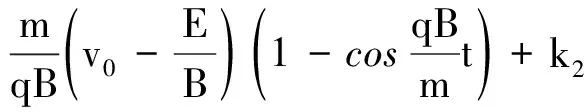
(17)

由初始条件x|t=0=0，y|t=0=0可知k1=k2=0.

至此，得到x，y的最终表达式

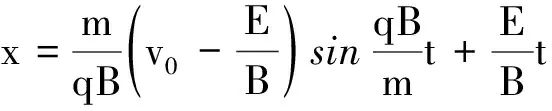
(18)

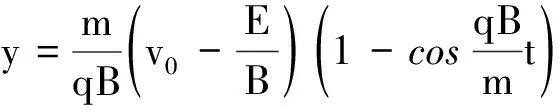
(19)

从式(18)、(19)可以看出，粒子在x轴上的运动为简谐运动和匀速直线运动的合成，而在y轴上则做简谐运动.运动的周期为

振幅为

在一个周期T内，竖直方向的位移为y=0，而水平方向的位移为

在一个周期内粒子的实际运动轨迹为

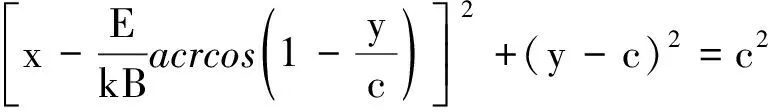
(20)

其中

通过理论求解得到的结果与考题提供的条件和最终答案完全一致，说明了该方法的正确性，同时通过理论求解，使得我们能够从本质上认识这种运动情形.